基于混合阻尼控制的車(chē)輛半主動(dòng)懸架可調(diào)性研究＊

郭孔輝 王金珠 郭耀華 薛 冰

（1.吉林大學(xué) 汽車(chē)仿真與控制國(guó)家重點(diǎn)實(shí)驗(yàn)室；2.湖南大學(xué) 汽車(chē)車(chē)身先進(jìn)設(shè)計(jì)制造國(guó)家重點(diǎn)實(shí)驗(yàn)室）

1 前言

天棚阻尼控制作為經(jīng)典的控制邏輯，由于其算法簡(jiǎn)單工程易于實(shí)現(xiàn)且魯棒性較強(qiáng)，現(xiàn)已經(jīng)廣泛應(yīng)用于中高端汽車(chē)的半主動(dòng)控制系統(tǒng)。但天棚控制從原理上只能以降低汽車(chē)安全性來(lái)改善乘坐舒適性，而混合控制策略則在天棚控制的基礎(chǔ)上結(jié)合地棚控制，能在安全性和乘坐舒適性之間折衷，從而使懸架的整體性能得到提升。

對(duì)混合控制策略的研究主要集中在如何使天棚、地棚阻尼系數(shù)Csky、Cgnd及阻尼分配系數(shù)α與整車(chē)進(jìn)行匹配。文獻(xiàn)[1]采用免疫優(yōu)化算法對(duì)α及Csky的匹配進(jìn)行了一些探討和研究。而現(xiàn)代車(chē)輛懸架系統(tǒng)通常采用與路面和車(chē)速自適應(yīng)的控制策略，這時(shí)更關(guān)注懸架的可調(diào)性[2]。為此，本文通過(guò)優(yōu)化懸架參數(shù)確定了懸架剛度ks和Csky及Cgnd，使混合控制策略下車(chē)輛半主動(dòng)懸架有一個(gè)合適的可調(diào)范圍。通過(guò)改變參數(shù)α使車(chē)輛的平順性和安全性相對(duì)于被動(dòng)懸架有所改善。

2 懸架模型的建立

2.1 路面輸入

分析懸架性能時(shí)首先要用到路面的隨機(jī)輸入。當(dāng)車(chē)速為定值時(shí)，速度的時(shí)域功率譜即為白噪聲信號(hào)[3]，本文采用積分濾波白噪聲法產(chǎn)生C級(jí)隨機(jī)路面作為輸入。

式中，xr為路面垂直方向位移；n0為參考空間頻率，n0=0.1m-1；Gxr（n0）為路面不平度系數(shù)；v0為汽車(chē)行駛速度；ω（t）為單位白噪聲；f0為下截止頻率。

在Simulink環(huán)境下采用積分濾波白噪聲法產(chǎn)生如圖1所示C級(jí)隨機(jī)路面。

2.2 1/4車(chē)輛懸架簡(jiǎn)化模型

在研究基于天棚、地棚半主動(dòng)懸架混合控制策略時(shí)，采用如圖2所示的1/4車(chē)輛懸架簡(jiǎn)化模型，即忽略了輪胎阻尼，用定剛度的彈性元件來(lái)近似代替輪胎。其中，mb為簧載質(zhì)量，mw為非簧載質(zhì)量，ks為懸架剛度，kt為輪胎剛度，c為懸架阻尼系數(shù)，z0、zw和zb分別為路面輸入、輪胎和車(chē)身的垂直位移。

由牛頓第二定律得到2自由度1/4車(chē)輛懸架垂向運(yùn)動(dòng)微分方程:

實(shí)際上理想的天棚、地棚阻尼器不存在，半主動(dòng)懸架簧載和非簧載質(zhì)量之間通過(guò)一個(gè)CDC（Continuous Damping Control）減振器來(lái)衰減振動(dòng)。圖3為實(shí)際1/4車(chē)輛半主動(dòng)懸架2自由度簡(jiǎn)化模型，其中cs為CDC減振器阻尼系數(shù)。

由牛頓第二定律得到其運(yùn)動(dòng)微分方程:

3 混合控制策略的實(shí)現(xiàn)

混合控制策略綜合天棚控制策略和地棚控制策略，使車(chē)輛舒適性和安全性都得到了改善。混合控制策略的基本思想是在簧載質(zhì)量和非簧載質(zhì)量上加一個(gè)與慣性系鏈接的阻尼器，產(chǎn)生的阻尼力分別與車(chē)身和輪胎的垂直運(yùn)動(dòng)速度成正比，能起到同時(shí)衰減車(chē)身和輪胎振動(dòng)的目的。

由于理想的慣性系不存在，因此只能以天棚、地棚模型為指導(dǎo)，結(jié)合半主動(dòng)懸架的CDC減振器可調(diào)范圍來(lái)研究一種混合控制算法，通過(guò)調(diào)節(jié)阻尼系數(shù)使減振器產(chǎn)生的阻尼力同時(shí)與車(chē)身和輪胎絕對(duì)速度成正比，從而使車(chē)輛的舒適性和安全性都能得到改善。

本文采用一種連續(xù)的混合阻尼控制策略，控制算法如下:

式中，Cs、Cg為實(shí)際天棚、地棚阻尼系數(shù)；Csky、Cgnd為理想天棚、地棚阻尼系數(shù)；Cmax、Cmin為CDC減振器可調(diào)的最大、最小阻尼系數(shù)。

通過(guò)調(diào)整阻尼分配系數(shù)α，可改變天棚控制力和地棚控制力在混合控制策略中所占的比重，使汽車(chē)能夠根據(jù)實(shí)際行駛工況和路面變化來(lái)改變懸架的阻尼控制規(guī)律，保證了懸架在任何工況下的最優(yōu)性能。

4 懸架參數(shù)匹配

4.1 懸架剛度的匹配

在被動(dòng)懸架中，彈簧剛度和減振器阻尼系數(shù)固定不變，因此設(shè)計(jì)被動(dòng)懸架時(shí)，只需根據(jù)實(shí)際要求在車(chē)輛舒適性和安全性之間取一個(gè)折衷[5]。而基于混合控制策略的半主動(dòng)懸架，如果懸架參數(shù)選擇不當(dāng)，則會(huì)使車(chē)輛的舒適性或安全性可調(diào)范圍很小，甚至?xí)?dǎo)致某一方面的惡化。因此，在半主動(dòng)懸架的設(shè)計(jì)過(guò)程中，懸架的參數(shù)選擇非常重要。

根據(jù)1/4車(chē)輛的垂向運(yùn)動(dòng)微分方程 （2）、方程（3）和混合控制算法公式（4），在 Simulink 環(huán)境下搭建了1/4車(chē)輛的被動(dòng)懸架和半主動(dòng)懸架模型，并采用上述積分濾波白噪聲法產(chǎn)生的C級(jí)隨機(jī)路面作為輸入。仿真結(jié)果將車(chē)身加速度z¨b、懸架動(dòng)撓度zw-zb及車(chē)輪動(dòng)載荷Fd輸出到Matlab工作空間做性能分析。懸架的基本參數(shù)如表1所列，其中減振器阻尼為被動(dòng)懸架阻尼，懸架剛度為待優(yōu)化值。

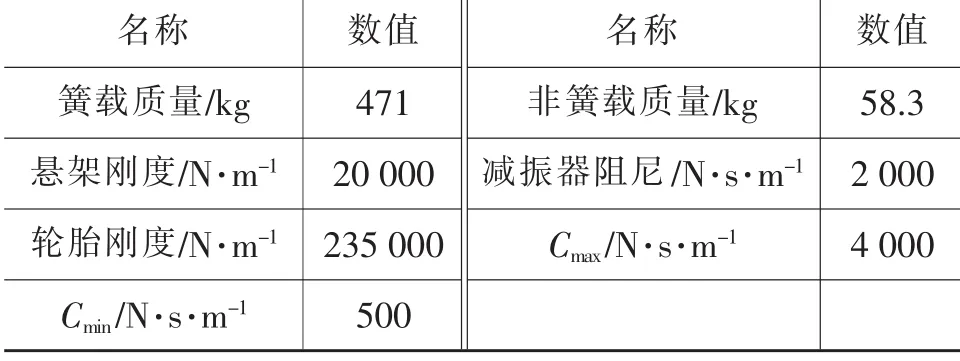
表1 被動(dòng)/半主動(dòng)懸架模型主要參數(shù)

考慮到在各種行駛工況下對(duì)汽車(chē)平順性的不同要求，首先建立如下目標(biāo)函數(shù):

式中，q為權(quán)系數(shù)，取值大時(shí)趨近于平順性，取值小時(shí)趨近于安全性；i起比例調(diào)節(jié)作用，使汽車(chē)的安全性和平順性評(píng)價(jià)指標(biāo)達(dá)到同一數(shù)量級(jí)便于比較；N為采樣數(shù)據(jù)長(zhǎng)度。

為分析懸架剛度對(duì)平順性和安全性可調(diào)范圍的影響，將懸架剛度ks和阻尼分配系數(shù)α視為兩個(gè)獨(dú)立的變量，ks和 α 分別從5000～30000 N/m和0～1之間分為若干等份，將ks和α進(jìn)行多次賦值，每賦值一次進(jìn)行一次仿真。在分析平順性可調(diào)范圍時(shí)令q=1，分析安全性時(shí)令q=0。半主動(dòng)懸架和被動(dòng)懸架的目標(biāo)函數(shù)值之差H=JS-JP為懸架的改善系數(shù)，當(dāng)H＜0時(shí)懸架相應(yīng)性能得到改善。本文將ks和α都分為50等份，經(jīng)過(guò)2500次仿真得到2500個(gè)H值并繪制H特性圖。H特性圖顯示了在不同ks值下，懸架在α值從0～1改變時(shí)其平順性Hr和安全性Hs的變化特征及范圍。

圖4和圖5為α變化時(shí)Hr-ks和Hs-ks特性曲線(xiàn)，圖4自上向下α從1～0逐漸減小，ks取值在22500～29000 N/m之間時(shí)平順性可得到比較明顯的改善，且α=0時(shí)平順性變化較小；圖5自上向下α從 0～1逐漸增大，當(dāng) ks在22500～30000 N/m 變化時(shí)安全性改善比較明顯，且α=1時(shí)安全性變化較小。

ks的取值要使在α變化時(shí)安全性和平順性相對(duì)被動(dòng)懸架都能得到改善，且當(dāng)平順性最好時(shí)安全性變化較小，安全性最好時(shí)平順性變化較小。圖5顯示當(dāng)ks＞22500 N/m時(shí)，增大ks可使安全性變好；圖4顯示當(dāng)ks＞26000 N/m時(shí)，平順性隨著ks的增加逐漸變差。本文優(yōu)先考慮平順性，因此ks比較理想的取值為26000 N/m。

4.2 Csky、Cgnd的匹配

在確定Csky、Cgnd時(shí)，本文首先由經(jīng)驗(yàn)公式C=給Cgnd初步取一個(gè)值，其中，C為理想天棚（地棚）阻尼系數(shù)，m為簧載（非簧載）質(zhì)量，k為懸架（輪胎）剛度。然后對(duì)Csky從500～10000 N·s/m每隔500 N·s/m分段賦值，分析懸架Hr和Hs在α從0～1之間取值時(shí)的變化[7]。

由經(jīng)驗(yàn)公式 Cgnd=并帶入懸架參數(shù)可得到理想地棚阻尼系數(shù)Cgnd的初始值CG=3701.4 N·s/m。

圖6為Csky取不同值時(shí)懸架的Hr特性圖，可看出Csky變大時(shí)懸架Hr曲線(xiàn)逐漸改善，即α=1時(shí)懸架平順性改善較好。從圖6、圖7可以看出，當(dāng)Csky＞4500 N·s/m時(shí)懸架Hr和Hs曲線(xiàn)幾乎不再變化。本文Csky取臨界最大值4500 N·s/m。

分析 Cgnd時(shí)，取 Csky=4500 N·s/m， 對(duì) Cgnd從500～10000 N·s/m每隔50 N·s/m分段賦值。圖8和圖9顯示，隨著Cgnd增大懸架Hr和Hs特性都逐漸變好，但當(dāng) Cgnd＞6000 N·s/m 時(shí) Hr、Hs曲線(xiàn)幾乎都不再變化。因此Cgnd取臨界最大值6000 N·s/m。

4.3 參數(shù)驗(yàn)證

根據(jù)以上確定的參數(shù)，在simulink環(huán)境下建立基于混合控制策略的車(chē)輛半主動(dòng)懸架模型，路面輸入采用白噪聲積分法產(chǎn)生的C級(jí)隨機(jī)路面，車(chē)速為40 km/s[8]。圖10為α=1時(shí)半主動(dòng)懸架與被動(dòng)懸架的車(chē)身加速度對(duì)比，圖11為α=0時(shí)半主動(dòng)懸架與被動(dòng)懸架非簧載質(zhì)量加速度對(duì)比，圖12顯示了平順性指標(biāo)Hr隨α的變化曲線(xiàn)，圖13顯示了安全性指標(biāo)Hs隨α的變化曲線(xiàn)。Hs-α曲線(xiàn)同時(shí)也說(shuō)明使安全性指標(biāo)Hs最好的α值不一定是0。本文大概在α=0.5時(shí)安全性達(dá)到最好。

從以上仿真曲線(xiàn)來(lái)看，根據(jù)實(shí)際路況調(diào)整α可以快速實(shí)現(xiàn)使車(chē)輛傾向于平順性或傾向于安全性，因此不管車(chē)輛行駛在何種路面或工況，都能始終保持車(chē)輛駕駛性能最佳。

5 結(jié)束語(yǔ)

討論了基于混合控制的車(chē)輛半主動(dòng)懸架可調(diào)性與懸架剛度、理想天棚地棚阻尼系數(shù)的關(guān)系。把懸架簧載質(zhì)量加速度和懸架動(dòng)撓度的加權(quán)加速度均方根值作為平順性指標(biāo)，非簧載質(zhì)量加速度均方根值作為安全性指標(biāo)，通過(guò)simulink仿真得到在α變化時(shí)K、Csky和Cgnd取值對(duì)懸架可控范圍的影響。經(jīng)分析對(duì)比Hr、Hs特性圖，最終確定了與本車(chē)參數(shù)相匹配的K、Csky和Cgnd，確保了車(chē)輛可根據(jù)實(shí)際車(chē)速和路況通過(guò)改變?chǔ)羴?lái)選擇傾向于平順性或安全性。

1 殷智宏，郭孔輝，宋曉琳.基于辨識(shí)模型的半主動(dòng)懸架控制策略研究.湖南大學(xué)學(xué)報(bào)，2010，37（12）:1～10.

2 喻凡，郭孔輝.車(chē)輛懸架的最優(yōu)自適應(yīng)與自校正控制.汽車(chē)工程，1998，20（4）:1～9.

3 ESLAMINASAB N,GOLNARAG HIF.A semi-active control strategy for vibration isolation to improve the ride comfort of vehicle.International Journal of Modelling，Identification and Control,2009,7（3）:281～293.

4 嚴(yán)天一，劉大維，師忠秀，等.基于基于地棚控制的半主動(dòng)懸架車(chē)輛道路友好性仿真.農(nóng)業(yè)機(jī)械學(xué)報(bào)，2007，38（1）:12～16.

5 余志生.汽車(chē)?yán)碚?北京:機(jī)械工業(yè)出版社，2009.

6 趙研，寇發(fā)榮，方宗德.汽車(chē)天棚控制半主動(dòng)懸架模型仿真與性能分析.計(jì)算機(jī)仿真，2006，23（11）:233～236.

7 顧信忠，張鐵山.減振器阻尼比的確定.農(nóng)業(yè)裝備與車(chē)輛工程，2010，19（12）:28～31.

8 中國(guó)國(guó)家標(biāo)準(zhǔn)局.GB/T 4970-2009.汽車(chē)平順性試驗(yàn)方法.北京:中國(guó)標(biāo)準(zhǔn)出版社，2009:1～16.