計算機繪制三鉸拱橋結構的影響線
李 彤, 李銀山
(1.華東理工大學 機械與動力工程學院,承壓系統與安全教育部重點實驗室,上海200237;2.河北工業大學力學系,天津300130)
0 引言
影響線是“結構力學”中重要概念,在求解結構受移動荷載(如橋梁上的汽車、列車等荷載,房中吊梁所承受的吊車荷載)作用下指定量值時有廣泛的應用,是確定最不利荷載位置的有效方法。所謂影響線是:當一個指向不變的單位集中豎向荷載沿結構移動時,表示某一指定量值變化規律的圖形。靜力法和機動法是繪制影響線的基本方法。由于三角拱的軸線為曲線,用上述兩種方法很難準確而快捷地繪圖。而當前的“結構力學”教材中很少涉及三鉸拱的影響線繪制。但拱結構在橋梁工程專業有廣泛的應用。因此,尋求精確、方便、快捷的途徑,對教學、科研都有幫助的工具是我們一直以來的努力目標。
現代計算機技術的出現可以很好地解決上述問題。Maple、Matlab等具有符號計算、數值計算、圖形處理等功能。語言簡單、界面友好,操作方便。特別是在提高計算精度方面是手算不能比的。因此探索如何將知識型、技能型人才教育模式向創造型、發明型人才培養方法的轉型,以實際行動回答“錢學森之問”,李銀山教授成功地開創了這方面的先河,編寫了《Maple材料力學》等面向能力培養的教材[1]。學生可以形象,直觀地看到理論公式的求解過程。增強了學生對理論的理解,對新問題的探索能力,激發學生的學習興趣。夏健明[2]利用Excel功能繪制了三鉸拱的內力圖。
本文提出用Maple軟件編程,計算一個三鉸拱的支座約束力、內力、畫出約束力及內力的影響線。論述了程序設計過程。
1 畫三鉸拱影響線的步驟
平面三鉸拱在單位豎向移動載荷作用下,如圖1所示,試分別繪制對支座垂直約束力VA、支座水平約束力H、彎距MK、剪力QK和軸力NK的影響線圖[3-5]。
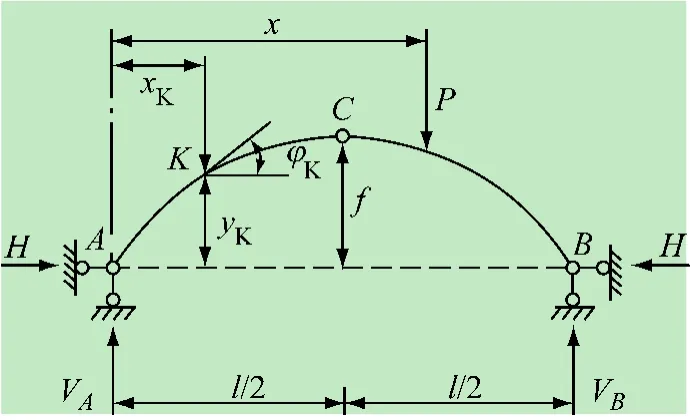
圖1 三鉸拱約束力計算簡圖
1.1 支座約束力的計算[6]
三鉸拱是由兩根曲桿與地基之間按“三剛片規則”組成的靜定結構,共有6個未知約束力,分別取左半拱和右半拱為隔離體,列6個平衡方程就可以求出6個未知約束力。考慮到載荷的移動性應該分單位豎向載荷在左半拱或者右半拱兩種情況分別求支座約束力。
單位豎向移動載荷在左、右半拱時,受力如圖2、3所示,分別取左半拱和右半拱為研究對象,按∑Fx=0,∑Fy=0,∑MC=0,列6個方程就可求出約束力。
繪制對稱三鉸拱約束力的影響線時,三鉸拱豎向約束力的影響線與相應簡支梁的約束力影響線完全相同,VA=,如圖 5(b)所示。P

而推力H的影響線可由相應簡支梁截面C的彎距影響線除以拱高而得到,如圖5(c)所示。
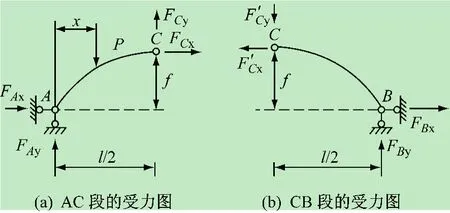
圖2 當荷載作用在AC段時受力分析圖
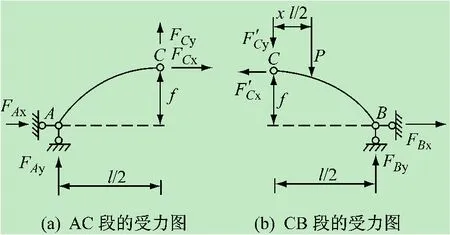
圖3 當荷載作用在CB段時受力分析圖
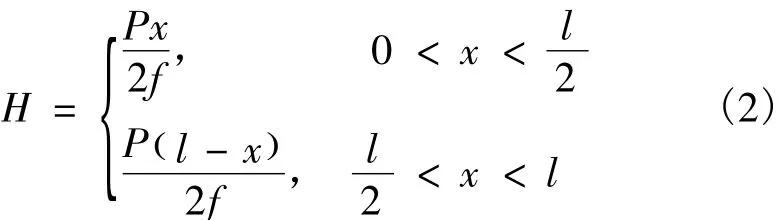
1.2 內力的計算[7-12]
約束力求出后,用截面法即可求出拱上任一橫截面的內力。任一橫截面K的位置可由其形心的坐標xK、yK和該處拱軸切線的傾角φK確定內力。在拱中,通常規定彎矩的符號以使拱內側受拉為正。由圖4所示隔離體,可求得截面K的彎距MK、剪力QK和軸力NK。

圖4 三鉸拱內力
任一截面K的內力:
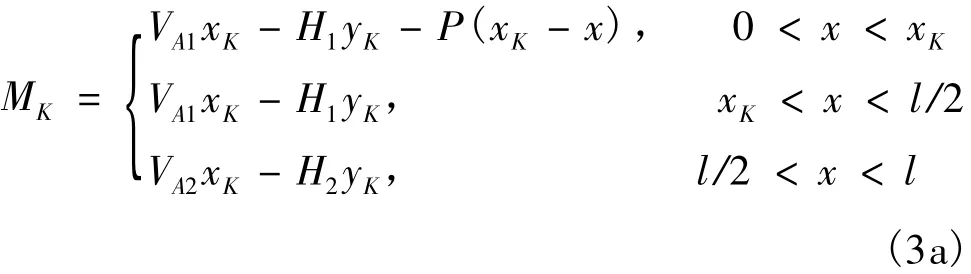
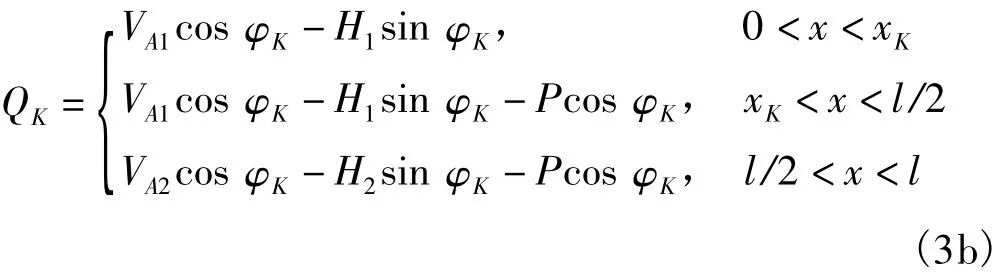
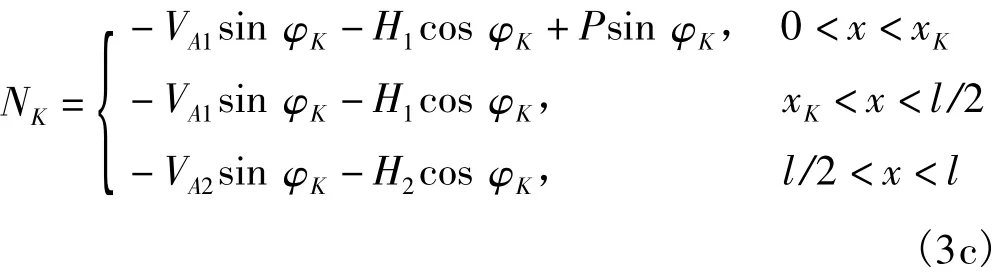
三鉸拱任一截面K的彎矩MK的影響線如圖5(d)所示,剪力QK的影響線如圖5(e)所示,軸力NK的影響線如圖5(f)所示。
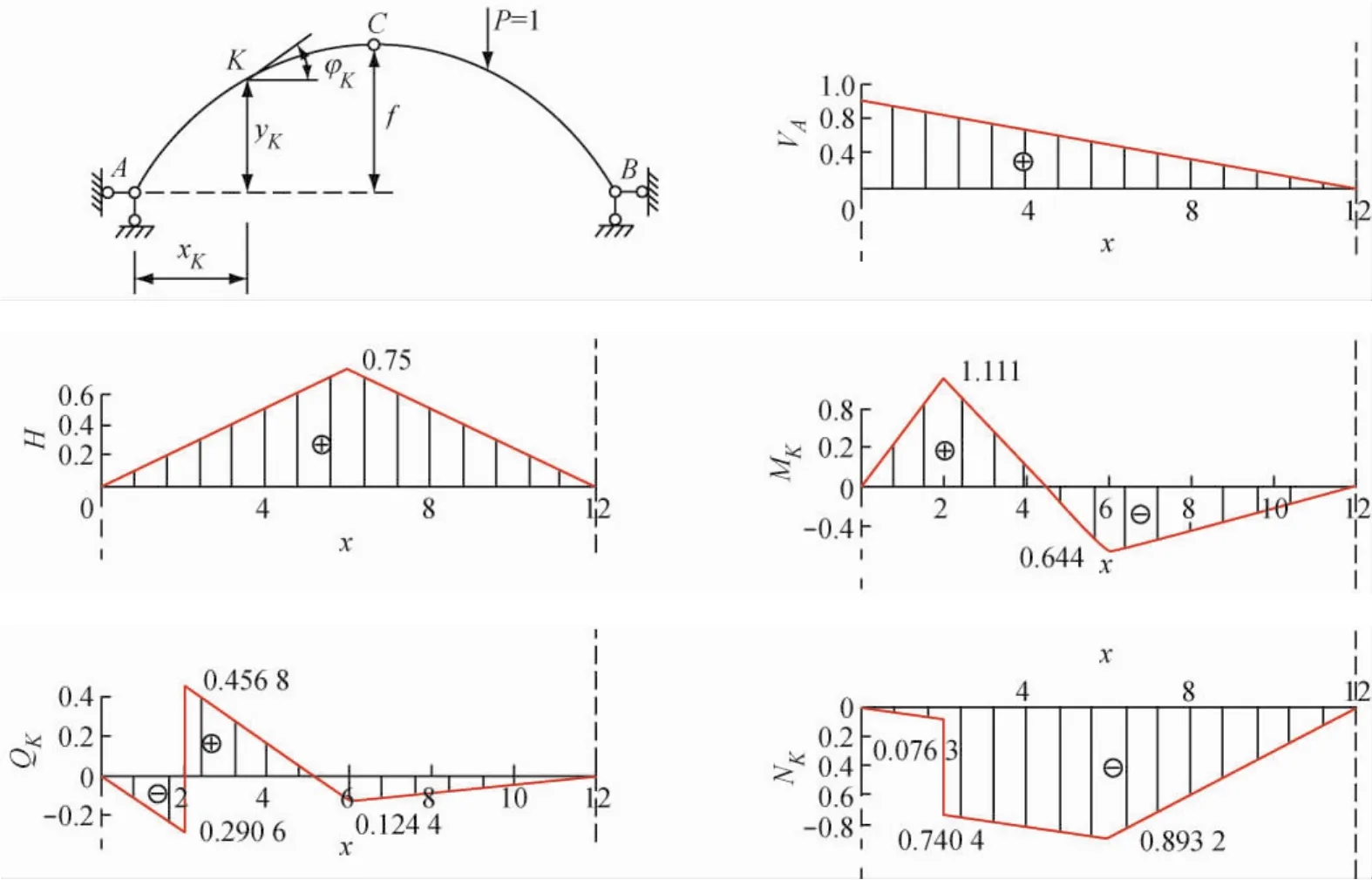
圖5 三鉸拱的約束力及內力影響線
2 計算機畫三鉸拱影響線實例
2.1 程序流程圖(見圖6)

圖6 三鉸拱程序流程圖
2.2 Maple程序
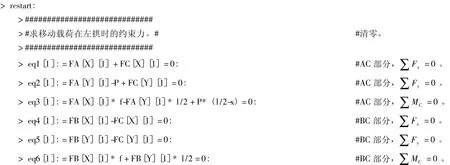


3 結語
用Maple語言編程,給出約束力和內力的分段解析函數。繪制三鉸拱橋結構,在豎向移動載荷作用下,對水平支座約束力,垂直支座約束力,任意截面上彎矩,剪力和軸力影響線。實例說明所編的程序,精確性高,可視化效果好,可操作性強,大大提高了計算效率。所編的程序通用性強,可進一步推廣,擴充其應用范圍[13-15]。本文是以對稱三鉸拱為例,同樣可以推廣到非對稱問題、超靜定等問題中。
[1] 李銀山.Maple材料力學[M].北京:機械工業出版社,2009.
[2] 夏健明.用Excel繪制三鉸拱的內力圖[J].力學與實踐,2010,32(4):104-1060
[3] 孫文彬.三鉸拱彎矩影響線的圖解法[J].力學與實踐,2002,24(1):57-58.
[4] 李廉錕.結構力學[M].北京:高等教育出版社,1979.
[5] 李照眾,徐中秋,王立彬.ANSYS對拱橋內力影響線計算分析[J].山西建筑,2007,33(33):309-310.
[6] 李 彤,李銀山.用計算機對三鉸拱橋結構靜力分析[J].實驗室研究與探索,2011,30(11):48-51.
[7] 戴仁杰.板拱橋的受力分析[J].結構工程師,1997(1):2-4.
[8] 崔清洋.三鉸拱內力分析的計算機方法[J].農業科學研究,1993(1):32-42.
[9] 張永清,李滿囤.拋物線斜板拱橋受力分析[J].煙臺師范學院學報,2001(2):103-109.
[10] 張永清,賈雙盈.拋物線斜板拱橋的內力計算[J].西北建筑工程學院學報,2001(2):17-23
[11] 卞 華,歐 莉.平鉸拱受力分析的迭代法[J].鄭州工業大學學報,2001(1):43-45
[12] 李新平,陳 湖,張 勇.拋物線拱的內力精確計算實用公式[J].科學技術與工程,2010(6):1453-1457.
[13] 李新平,鄧德員,張云帆.拋物線拱變位引起的內力分計算一般公式[J].科學技術與工程,2011(6):1388-1391.
[14] 程 進,江見鯨,商汝誠,等.拱橋結構極限承載力的研究現狀與發展[J].公路交通科技,2002(4):57-59.
[15] 項海帆,劉光棟.拱結構的穩定與振動[M].北京:人民交通出版社,1991.

