關聯維在砂體儲層預測上的應用

李小霞，文曉濤，楊小江

（1.成都理工大學地球物理學院，四川成都 610059；2.中海石油有限公司深圳分公司研究院，廣東深圳 518067）

分形幾何（Fractal geometry）是20世紀70年代由法國數學家B.B.Mandelbrot創立的，它揭示了自然界中所形成的無規則的內在規律，已廣泛應用于其它學科[1]。目前，在地震資料處理中，從地震道中提取屬性參數來進行巖性與儲層含油氣特征研究，是地震資料處理的一種主要的技術方法。但是在我們從地震道中進行屬性參數提取時，大部分都是基于線性分析理論。而實際上，地震道是一個典型的非線性時間序列，在標度范圍內普遍具有標度不變性和自相似性[2]。因此，基于動力學非線性理論，利用非線性時間序列分析的方法和技術來進行地震道屬性參數提取才會對地震信息的合理利用更有利。

在石油勘探中用于計算地震記錄時使用的主要是關聯維，它反映了以一定的嵌入維數為尺度對地震序列進行剖分，若剖分后各段地震序列之間的相似性好，則關聯維就增大，否則相反。含油氣層與不含油氣層地震序列經剖分后各小段地震序列之間相似性有差異，即關聯維的大小反映了處理時窗內地層變化復雜程度。由于地質構造和巖性的復雜多變，使得地震反射信號極不規則[3-5]。因此，關聯維數的大小反映了地震反射系列的復雜程度。本文主要研究和提取的地震屬性參數就是動力學非線性系統中不變量—關聯維。

1 地震屬性關聯維求取原理

由于地質構造和巖性的復雜多變，導致地震反射信號極不規則。因此認為地震道是一個混沌時間系列，具有介于一維和二維之間的分維數，這個分維數可以用重構相空間的方法來確定。重構一個相空間的目的使這個時間系列在一個合適的空間坐標中能夠顯示出混沌吸引子的結構。計算出的分維值就是地震道的關聯維，常用D表示，它對油氣層的反映較為直接而敏感。D值取決于地震道的波動形態，儲集層中是油、是氣、還是水，有不同的波阻抗，產生不同的反射系數，就會有不同的波形，因此就會有不同的D值[4-6]。

1.1 相空間重構

將地震道針對目的層開時窗，設地震道的采樣點數為n，某道的采樣點可以表示為：

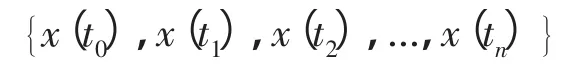
采用延遲坐標法將其重構組成一個m維的向量空間xN｛｝，即：

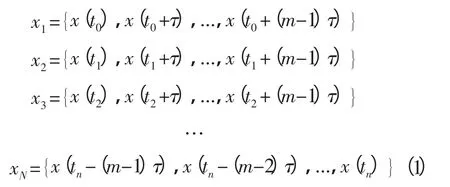
這是按采樣間隔τ順序構成的向量。這實際上相當于移動時窗，時窗寬度為m個樣，即為（m-1）τ。N=n-（m-1）τ為重構向量數。

1.2 計算相關函數

建立相空間后，求取任一點對xi，xj之間的歐氏距離Lij：

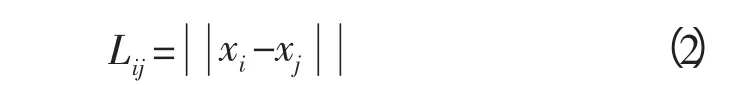
任意設定一個標度r，并統計距離小于r的一切點對的數目在全體點對數（N2）中的比例，其中N為相點數。

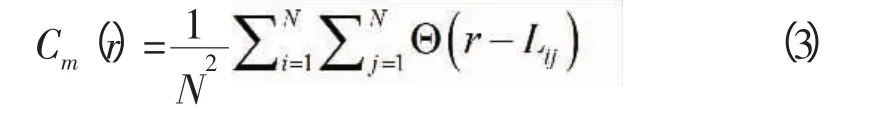
考慮到度量空間距離的對稱性，（3）式可進一步寫成：

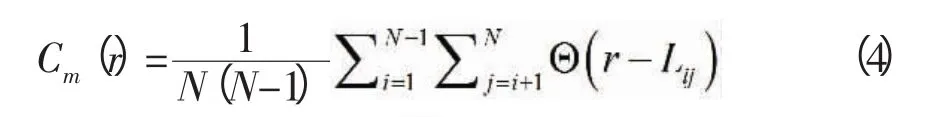
上式為關聯積分，式中 （x）為Heaviside函數，即：

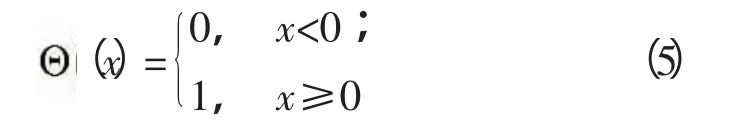
1.3 求關聯維數

r選擇合適的空間時，C（r）隨r呈冪級數形式變化，即：

取對數有

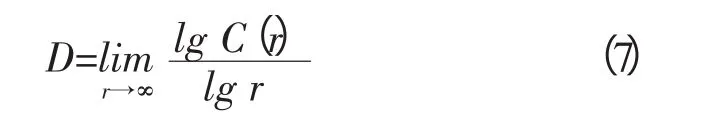
2 無標度區間的確定

在實際計算中，首先，標度r的取值要適中。為保證r的取值在無標度區間內，r值存在滿足條件：

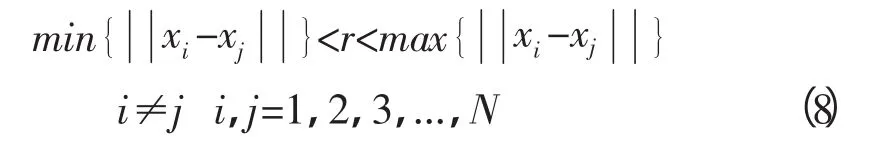
其次，由于信號采集的數據長度也會影響到參加數據擬合的點數，從而影響到無標度區間的確定。因此綜合上述兩個方面，計算方法如下：計算出重構相空間中兩點距離的最大值和兩點距離的最小值設標度的單位長度為Δt（Δt的取值應根據不同的分析對象分別考慮），取步長k=ss，標度r的方程為：

經過取不同的ri（i=j，j+1，...，n，j≥1）能夠得到一系列的Cm（ri）；將得到的ri和Cm（ri）取對數用最小二乘法進行擬合，得到圖像的斜率值即為該系統的關聯維數。

3 理論模型數值分析

針對研究砂體儲集層的關聯維情況，建立了兩套理論地質模型。砂體地質模型1（見圖1（a）），圍巖速度為4 000 m/s，儲層砂體速度為3 500 m/s；模型2（見圖1（b）），蓋層泥巖速度為 3 300 m/s，下部砂層速度為3 000m/s，中間儲集層速度為2 800 m/s。采用頻率波數域波動方程數值模擬方法對地震波場進行正演模擬（見圖1（c）、圖1（d）），不僅求解速度快且很好地保留地震波場的運動學和動力學特征[8，9]。

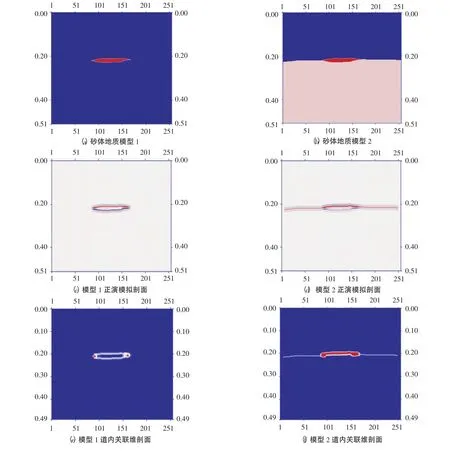
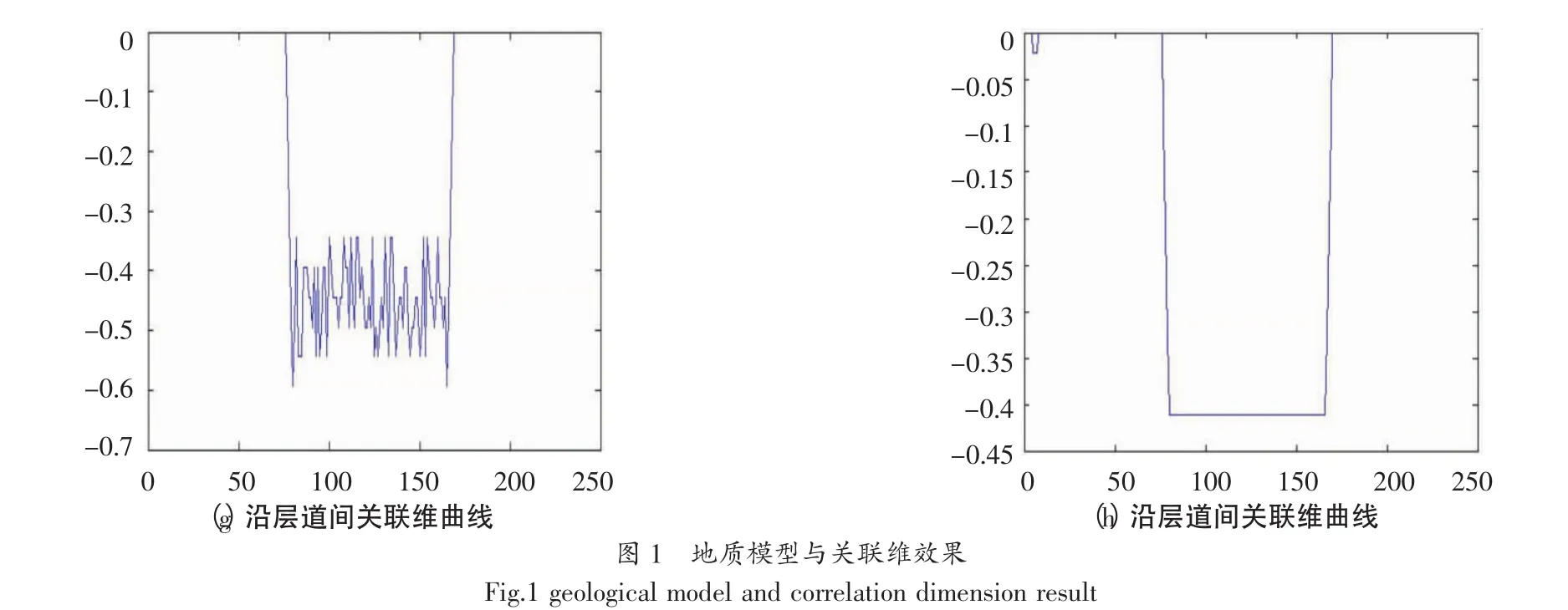
圖1（e）和圖1（f）為對理論模型計算出的道內關聯維剖面。圖1（e）表明，在砂體邊界關聯維值明顯降低，薄層砂體的頂底位置明顯。而在圖1（f）則可看出，關聯維可識別薄層砂體及泥砂層分界面，但不能分辨出厚層砂體的存在。圖1（g）和圖1（h）為沿層道間關聯維曲線，在儲集層位置關聯維值降低。

4 應用實例及效果

通過關聯維計算結果對已鉆井區進行檢驗。通常選擇過已知井的過井剖面，根據砂層和油層的厚度確定適當的時窗（為確保其精度，所取的時窗一般不超過15 ms），來驗證上述計算結果是否能有效地反映儲層和油氣的變化，并通過調整時窗等參數，在保證與鉆井完全吻合的前提下，再進行未知區的預測。

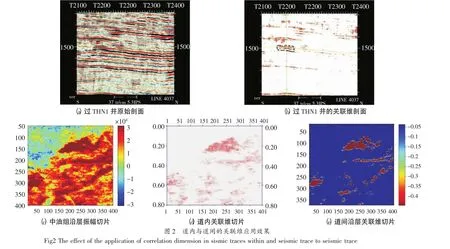
本文研究區域為塔河YY區，該區三疊系構造較平緩，主要受N-E向斷裂帶和鹽體的塑性活動控制，沿N-E方向延伸形成大型圈閉群。三疊系發育的儲層主要有上、中、下三油組的砂體。本文針對中油組砂體進行研究。圖2（a）為過THN1井剖面，單從原剖面上很難分辨砂體的發育程度及砂體的邊界；圖2（b）為沿地震道方向計算的關聯維過井剖面，則可以清楚識別砂體儲集層位置，且在砂體儲集層上其D值明顯降低。圖2（e）是對計算的道內關聯維數據體提取的沿層切片，圖2（d）為沿層（道間）方向計算的關聯維切片。比較圖2（e）和圖2（d）可知，沿層方向所得關聯維對砂體范圍顯示更清楚，并且在圍巖及儲集層砂體上的關聯維值基本穩定。

5 結論與建議

結合模型與實例分析證明，關聯維在砂體儲集層檢測上具有一定的效果。

（1）道內關聯維反映的是某時窗地震記錄的綜合信息，結合地質和鉆井進行綜合分析的基礎上，可以判別砂體的發育程度、確定砂體儲集層位置。但由于波形本身具有復雜性，造成砂體預測的多解性。

（2）道間關聯維反映的是道間巖性展布，因其受波形變化影響少，所以在圍巖及儲集層砂體上的關聯維值基本穩定，可清楚顯示砂體范圍。

（3）關聯維應用于儲層預測，其變化既可能是由于地層、儲層變化引起，也可能是含油氣造成的，因此在不同地區，應根據不同的地質模型，合理地進行儲集層預測和油氣檢測。

［1］H.S.Kim，R.Eykholt，J.D.Salas.Nonlineardynamics，delay times，and embedding windows［J］.Physica D，1999，（127）：48-60.

［2］隋少強，宋麗紅，李淑敏，等.分形理論在儲集層橫向預測和油氣層判斷中的應用［J］.新疆石油地質，2001，22（4）:342-344.

［3］文曉濤，賀振華，黃德濟.基于小波包變換與關聯維的儲集層檢測［J］.新疆石油地質，2007，28（5）：569-571.

［4］文曉濤，賀振華，黃德濟.基于小波包變換與關聯維的儲層檢測［G］.中國地球物理學會第22屆年會論文集，2006.

［5］黨建武，等.基于分形理論的地震信號空間序列分析［J］.西安石油學院學報（自然科學版），2003，18（4）：11-14.

［6］姜素華，等.地震道的分形維計算及在灘海地區油藏描述中的應用［J］.中國海洋大學學報，2006，36（5）：841-844.

［7］賈子文，等.分形理論中無標度區間的識別方法［J］.設計與研究機械，2012，11（39）：24-30.

［8］周懷來，等.各向異性介質儲層數值模擬及波場特征研究［J］.物探化探計算技術，2010，32（4）：345-353.

［9］陳可洋，楊微，吳清嶺，等.幾種地震波疊后深度偏移方法的比較［J］.勘探地球物理進展，2009，32（4）：257-260.