基于混合蛙跳算法的混凝土壩加權變形預報模型

王 偉，沈振中，鐘啟明

(1.南京水利科學研究院巖土工程研究所，江蘇南京 210029;2.江蘇弘盛建設工程集團有限公司，江蘇高郵 225600;3.河海大學水文水資源與水利工程科學國家重點實驗室，江蘇南京 210098)

基于混合蛙跳算法的混凝土壩加權變形預報模型

王 偉1，2，沈振中3，鐘啟明1

(1.南京水利科學研究院巖土工程研究所，江蘇南京 210029;2.江蘇弘盛建設工程集團有限公司，江蘇高郵 225600;3.河海大學水文水資源與水利工程科學國家重點實驗室，江蘇南京 210098)

利用混合蛙跳算法的優化特點，將大壩安全監控統計模型的求解轉換為多目標函數的優化問題;引入調整系數修正回歸因子，考慮調整系數與回歸因子之間的協調關系，利用混合蛙跳算法同步確定調整系數和回歸系數，建立基于混合蛙跳算法的混凝土壩加權變形預報模型。工程算例應用結果表明，該模型具有較優的中長期預報能力，可提高大壩安全監控統計模型的預報精度，在大壩安全監控領域具有一定的工程應用意義。

混凝土壩;大壩變形;群智能算法;混合蛙跳算法;加權變形預報模型

基于監測資料和壩工力學原理的大壩安全監控統計模型(以下簡稱統計模型)具有明確的物理意義，能夠較好地反映上游庫前水位、下游水位、氣溫等環境因素對壩體變形、壩基揚壓力等效應量的作用以及相互關系。統計模型的應用關鍵在于回歸系數的最優估計，常采用最小二乘法確定。在一般情況下，統計模型的預測精度較高，能夠歸納監測效應量的內在發展趨勢和判斷壩體的工作狀態。但在某些特殊情況下，如存在監測異常點、各環境因素之間存在多重相關性等，統計模型的預測精度較低［1-2］。針對最小二乘法的不足，許多學者提出了改進方法，如差值逐步回歸分析法、偏最小二乘法、門限回歸預測模型等［3］。

仿生算法和群智能算法具有較強的抗噪性和處理因素間相關特征的優越性，前者已大量應用于大壩安全監控領域的研究，如基于BP神經網絡、RBF神經網絡、遺傳算法以及改進型神經網絡的大壩安全監控預報模型，其預測精度均較高［4-6］;后者一般作為優化參數的工具，如采用群智能算法對支持向量機、神經網絡的計算參數進行優化，分別建立相應的大壩安全監控預報模型［7-9］。目前對于群智能算法與統計模型的融合研究較少，筆者曾將粒子群算法與統計模型及聚類算法相融合分別建立預報模型，其預測精度較高［10-11］。混合蛙跳算法是屬于群智能算法的分布式算法，本文利用混合蛙跳算法的優化性能隨機搜索加權統計模型的計算參數，以調整系數取代權重，并同步確定統計模型中的回歸系數和調整系數，最終建立基于混合蛙跳算法的混凝土壩加權變形預報模型。

1 混凝土壩加權變形預報模型

按受力成因，壩頂位移 δx可分為水壓分量f(H，wH)、溫度分量f(T，t，wT)、時效分量f(θ，wθ)。考慮各分量對模型的影響程度，以調整系數取代權重建立加權變形預報模型:

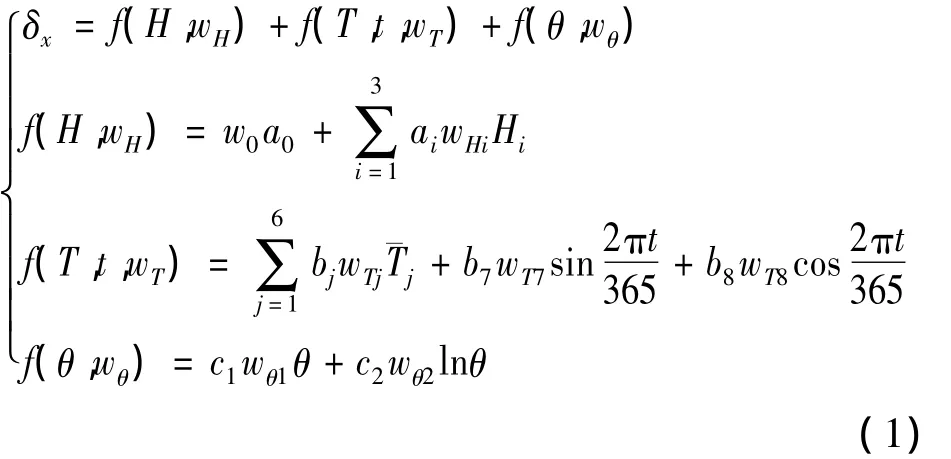
式中:H為庫前水位;T、t分別為氣溫和監測時間;θ為監測日至基準日的累計天數除以100;wH、wT、wθ為各分量因子的調整系數，記為 W=(wH，wT，wθ);ai(i=0，1，2，3)、bj(j=1，2，…，8)、c1、c2為分量因子的回歸系數，記為 A=(ai，bj，c1，c2)。

由式(1)可見加權變形預報模型是個多元非線性的數學模型，該模型在數據空間中存在全局優化極值。加權變形預報模型比統計模型更能反映大壩監測效應量的發展規律，可考慮水壓分量、溫度分量等對監測效應量的影響程度，從而全面地對大壩運行狀態進行評價。加權變形預報模型的求解一般先確定回歸系數，再采用主觀或客觀方法確定調整系數［12］。由于加權變形預報模型(式(1))的計算參數具有非線性特點，較難對其進行線性化處理，無法采用最小二乘法確定其值，且調整系數與回歸系數在求解過程中應一并考慮，分步計算顯然是不合理的。因此本文從極值優化角度出發，將加權變形預報模型轉換為優化模型進行求解。

2 加權變形預報模型的優化計算

2.1 優化模型的建立

若將調整系數W、回歸系數A同時視為一組待定的設計變量Q，分別以每個設計變量qj(j=1，2，…，M)作一個坐標軸，可形成M維實歐氏空間，記為RM。RM中的空間點稱為設計點，每個設計點的空間位置可看作設計變量的一組確定的解，代表具體優化問題的一組候選解，即RM中的每個設計點對應調整系數W、回歸系數A的一組待定解。若將擬合殘差平方和最小作為目標函數，將各時刻對應的壩頂水平位移和影響因素的監測值作為等式約束條件，將調整系數的變化范圍作為不等式約束條件，則加權變形預報模型可轉為具有約束條件的多目標優化問題:

式中:f(A，W，H，T，θ)為監控模型的目標函數;yi、為壩頂水平位移的實測值和模型計算的擬合值;n為監測數據樣本的容量;M為模型中回歸系數和調整系數的總數目。

式(2)所示模型的求解可轉換為極小值優化問題，即在RM中存在無數個設計點，每個設計點均對應回歸系數和調整系數的一組待定值。模型中計算參數的優化過程就是在設計空間RM內無窮多個設計點中，搜索一個既滿足所有約束條件，又使目標函數取得極小值的設計點，該設計點的空間位置就為調整系數、回歸系數的全局最優解。群智能算法以隨機搜索和迭代計算等為求解方式，而無需通過求解偏導、聯立方程組的方式求得，具有較強的靈活性。

2.2 混合蛙跳算法的優化實現

混合蛙跳算法的基本思想基于蛙群覓食過程，屬于分布式群智能算法［13］。在算法中蛙群落被劃分為若干組小群落，單蛙個體以隨機路徑跳躍式覓食，并記錄自身的覓食路徑。每完成一次覓食過程，單蛙個體首先在小群落之間交換食物地點信息，之后每個群落之間交換覓食路徑信息，確定該次覓食過程的最短路徑。最終經過若干次進化，確定蛙群至覓食地點的最優路徑信息，即優化問題的全局最優解。如何確定單蛙個體位置點的編碼形式是應用混合蛙跳算法的關鍵，針對不同類型的優化問題，其編碼形式有所不同。對于加權變形預報模型，位置點的編碼形式須與回歸系數、調整系數一致，位置點的變化區域受其取值范圍的制約。

在進化初始時刻，蛙群落中蛙總數為m。在調整系數、回歸系數取值范圍內隨機生成各單蛙個體xi(i=1，2，…，n)的位置點向量 Xi=(xi1，xi2，…，xij)(j=1，2，…，M)，每個單蛙xi在數據空間里的位置分別對應一組加權預報模型的待定解。若將蛙群落分成N組，每組蛙的規模為K(K=m/N)每組中單蛙xi的跳躍方向及跳躍步長由該組內最優路徑信息和最費時路徑信息所決定，則在RM中單蛙個體位置點的更新公式為式中:l為蛙群進化次數;R為(0，1)之間的隨機數;gl，j為第j組群落內最優單蛙個體的歷史位置向量;bl，ij、dl，ij分別為第j組群落內最差單蛙個體xi的歷史最差位置向量及本次進化過程中的跳躍步長向量;bl+1，ij為更新后最差單蛙個體xi的位置向量。

從式(3)和式(4)可知，在每次進化過程中小群落主要利用本組最優路徑信息對最差單蛙個體xi的位置點進行修正，并不改變該組其余單蛙個體的移動路徑，因此在計算初期各組蛙群的隨機搜索最優路徑的時間花費少，具有較高的局部優化效率。對于全局優化性能，混合蛙跳算法是通過各組蛙群之間優化信息的交流來實現的，即在每次進化結束后各組蛙群重新組合成一個大群落，并以各單蛙個體位置點對應的適應度信息的優劣再次劃分N組群落。如此循環進化后，最終確定回歸系數A、調整系數W的全局最優解。

單蛙適應度的定義形式與加權變形預報模型的求解目標相關。由式(2)可知，模型求解目標為擬合殘差平方和最小，相應的單蛙適應度Fl，k定義為壩頂水平位移的待測樣本實測值和模型擬合值的殘差平方和，即

因此式(5)所得解的值越小表示單蛙個體的適應度值越優，其在數據空間中的位置點向量越逼近回歸系數A、調整系數W的全局最優解。

基于混合蛙跳算法求解加權變形預報模型的計算步驟如下:

a.初始化各計算參數，依據回歸系數、調整系數的取值范圍隨機生成各單蛙個體位置點向量的初始值 X0，k。

b.由式(5)計算各單蛙個體的初始適應度F0，k。

c.根據適應度值大小對蛙群進行排序，并采取等間隔取數方式將蛙群劃分為N組。

d.對每組蛙群采用內部循環方式執行局部優化策略:由式(3)和式(4)對本組內最差單蛙個體的位置點向量進行修正，重新計算適應度Fl+1，k;若Fl+1，k＜Fl，k，表明修正后的位置點更接近模型的最優解，最差蛙個體接受修正后的位置信息，否則，隨機生成新的位置點向量;重新依據適應度值的優劣對該組蛙群進行排序，進入下一次的內部循環過程，直至循環結束。

e.對整個蛙群采用外部循環方式執行全局優化策略。首先將N組蛙重新歸并，再次依據各單蛙個體的適應度值大小對蛙群進行排序，并將蛙群劃分為N組。

f.返回步驟d。重復步驟d至 e，直至外部循環結束或滿足優化終止條件，最終輸出回歸系數A、調整系數W的全局最優近似解。

3 工程算例

某水庫是以發電為主，兼顧防洪、旅游、灌溉等綜合利用的大型水利樞紐。水庫正常蓄水位為108 m，相應庫容為178.4億m3。攔河壩為混凝土寬縫重力壩，最大壩高105m，全長466.5m。大壩自右至左共分26個壩段，右岸0～6號和左岸17～25號為非溢流壩段，河床7～16號壩段為溢流壩段。依據式(2)分別對右岸3號、河床16號壩頂水平位移建立加權變形預報模型。

應用VB匯編語言編制混合蛙跳算法的計算程序，其計算參數設置為:蛙群落的規模為1500，劃分組數N為50，每組內單蛙個體總數為30，外部循環總數為30，內部循環總數為25。在［－1，1］和［0，1］區間內隨機生成回歸系數、調整系數的初始解，作為各單蛙個體的初始位置點向量，最大跳躍步長設置為1。數據樣本為:以1986—1997年之間的觀測資料作為計算樣本，共計150組數據，其中以1986—1992年間的觀測數據作為訓練樣本，1993—1997年間的觀測數據作為待測樣本。

為了驗證加權變形預報模型的應用效果和可行性，另外建立相同回歸因子的線性統計監控模型，采用最小二乘法進行求解，并將計算結果進行比較。預報效果的檢驗指標采用平均絕對百分比誤差、均方誤差和平均絕對誤差以及待測樣本的擬合殘差平方和，共4個指標。經計算，兩種算法對于右岸3號、河床16號的預報指標如表1所示，預報過程線如圖1所示。

表1 待測樣本的預報指標對比

由表1和圖1可見，基于混合蛙跳算法的加權變形預報模型的統計指標值均比基于最小二乘法的統計模型的統計指標值小，表明混合蛙跳算法具有較優的數據挖掘能力。從預報過程可知，在預報初期最小二乘法和混合蛙跳算法的擬合精度大致相當。隨著預報時間的延長，混合蛙跳算法的擬合精度優于最小二乘法，表明最小二乘法的短期預測能力較強，但中長期預測能力較弱，而混合蛙跳算法在短期及中長期均具有較強的預測能力，對3號段和16號壩段的擬合殘差平方和分別降低36%和56%。可見通過調整系數對統計模型中回歸系數進行修正，利用混合蛙跳算法同步確定回歸系數、調整系數的最優解，能夠進一步擴展統計模型的預報能力，提高其預報精度。

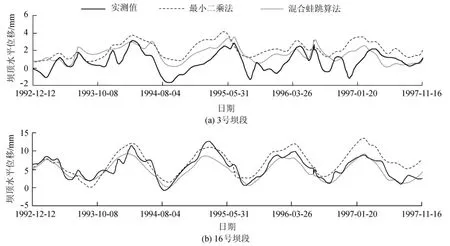
圖1 水平位移預報過程線對比

圖2為混合蛙跳算法的收斂過程線，可知混合蛙跳算法的隨機搜索能力較強，在計算過程的中后期就能夠逼近全局最優解，其算法收斂性能較優。

圖2 混合蛙跳算法的收斂過程

4 結語

混合蛙跳算法具有可調參數少、全局優化能力強的特點，目前主要應用于多目標函數的求解，將其應用于大壩安全監控領域，具有一定的工程應用價值，是對傳統監控方法的有益補充。工程算例結果表明，基于混合蛙跳算法的混凝土壩加權變形預報模型具有中長期預報能力，一方面通過調整系數修正回歸因子所包含的信息，另一方面依據調整系數和回歸系數的協同關系采用混合蛙跳算法同步優化求解，有效地擴展了統計模型的預報范圍，提高了模型的預報精度。文中混合蛙跳算法在每次迭代進化過程中，主要采用對最差單蛙個體位置點向量進行修正的局部更新策略，將該局部更新策略與粒子群算法、蟻群算法或遺傳算法的更新策略進行有效地結合以及對主要計算參數進行修正，是否能進一步提高變形預報模型的預報能力有待進一步的研究。

［1］楊杰，胡德秀，吳中如.大壩安全監控模型因子相關性及不確定性研究［J］.水利學報，2004(12):99-105.(YANG Jie，HU Dexiu，WU Zhongru.Multiple co-linearity and uncertainty of factors in dam safety monitoring model［J］.Journal of Hydraulic Engineering，2004(12):99-105.(in Chinese))

［2］龔曉雯，范磊.非線性分位點回歸方法在大壩安全監測中的應用［J］.河海大學學報:自然科學版，2011，39(1):99-103.(GONG Xiaowen，FAN Lei.Application of nonlinear quintile regression in dam safety monitoring［J］.Journal of Hohai University:Natural Sciences，2011，39(1):99-103.(in Chinese))

［3］何鮮峰，鄭東健，谷艷昌.大壩安全監控的門限回歸預測模型及其應用［J］.長江科學院院報，2007，24(3):20-22.(HE Xianfeng，ZHENG Dongjian，GU Yanchang.Dam safety monitoring threshold regression model and application［J］.JournalofYangtzeRiverScientific Research Institute，2007，24(3):20-22.(in Chinese))

［4］KIM Y S，KIM B T.Prediction of relative crest settlement of concrete-faced rockfill dams analyzed using an artificial neural network model［J］.Computers and Geotechnics，2008，35(3):313-322.

［5］蘇懷智，吳中如，溫志萍，等.基于模糊神經網絡和遺傳算法的大壩安全監控模型［J］.大壩觀測與土工測試，2001，25(1):10-12.(SU Huaizhi，WU Zhongru，WEN Zhiping，et al.Dam safety monitoring model based on fuzzy neuralnetwork and genetic algorithm ［J］.Dam Observation and Geotechnical Tests，2001，25(1):10-12.(in Chinese))

［6］魏海，楊華舒，武亮.基于人工神經網絡的重力壩安全可靠度分析［J］.河海大學學報:自然科學版，2011，39(4):415-420.(WEI Hai，YANG Huashu，WU Liang.Gravity dam safety reliability analysis based on artificial neural network［J］.Journal of Hohai University:Natural Sciences，2011，39(4):415-420.(in Chinese))

［7］姜諳男，梁冰.基于PSO-SVM的大壩滲流監測時間序列非線性預報模型［J］.水利學報，2006，37(3):331-335.(JIANG Annan，LIANG Bing.Nonlinear time series prediction model for dam seepage flow based on PSO-SVM［J］.Journal of Hydraulic Engineering，2006，37(3):331-335.(in Chinese))

［8］張磊，金永強，李子陽，等.CPSO-NN模型在大壩安全監控中的應用［J］.水利水電科技進展，2008，28(4):8-10.(ZHANG Lei，JIN Yongqiang，LI Ziyang，et al.Application of CPSO-NN model in dam safety monitoring［J］.Advances in Science and Technology of Water Resources，2008，28(4):8-10.(in Chinese))

［9］楊陽，王越.基于最優化溫度周期因子的壩體變形監測模型［J］.水利水電科技進展，2010，30(6):26-29.(YANG Yang，WANG Yue.Dam deformation monitoring model based on optimal temperature cycle factor［J］.Advances in Science and Technology of Water Resources，2010，30(6):26-29.(in Chinese))

［10］王偉，沈振中，王連慶.基于粒子群仿生算法的混凝土壩變形預報模型［J］.水利水電科技進展，2008，28(4):11-14.(WANG Wei，SHEN Zhenzhong，WANG Lianqing.Concrete dam deformation forecasting model based on PSO bionic algorithm ［J］.Advances in Science and Technology of Water Resources，2008，28(4):11-14.(in Chinese))

［11］王偉，沈振中，王連慶.基于粒子群聚類算法的大壩安全監控模型［J］.河海大學學報:自然科學版，2008，36(4):501-504.(WANG Wei，SHEN Zhenzhong，WANG Lianqing.Dam safety monitoring model based on PSO-fuzzy clustering algorithm ［J］.Journal of Hohai University:Natural Sciences，2008，36(4):501-504.(in Chinese))

［12］顧沖時，吳中如.大壩與壩基安全監控理論和方法及其應用［M］.南京:河海大學出版社，2006.

［13］ELBELTAGI E，HEGAZY T，GRIERSON D.Comparison among five evolutionary-based optimization algorithms［J］.Advanced Engineering Informatics，2005，19(1):43-53.

Weighted deformation forecast model for concrete dams based on shuffled frog leaping algorithm

WANG Wei1，2，SHEN Zhenzhong3，ZHONG Qiming1(1.Department of Geotechnical Engineering，Nanjing Hydraulic Research Institute，Nanjing210024，China;2.Jiangsu Hongsheng Construction Engineering Group Co.，Ltd，Gaoyou225600，China;3.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Hohai University，Nanjing210098，China)

By means of the optimization features of the shuffled frog leaping algorithm，the solution to the statistical model for dam safety monitoring was converted to the optimization of the multi-objective function.The adjustment coefficients were introduced to correct the change of the regression factors.Considering the relationship between the adjustment coefficients and the regression factors，the values of the adjustment coefficients and the regression factors were synchronously determined by use of the shuffled frog leaping algorithm.A weighted deformation forecast model for a concrete dam was established based on the shuffled frog leaping algorithm.The engineering examples show that the proposed model has superior long-term forecasting ability，and it may enhance the forecasting accuracy of the traditional statistical model for dam safety monitoring.It has certain application value for engineering in the field of dam safety monitoring.

concrete dam;dam deformation;swarm intelligence optimization algorithm;shuffled frog leaping algorithm;weighted forecast model

TV642;TV698.1+1

A

1006-7647(2013)02-0037-05

10.3880/j.issn.1006-7647.2013.02.008

國家自然科學基金(51109141);中央公益性科研院所青年基金(Y311005)

王偉(1979—)，男，江蘇高郵人，工程師，博士，主要從事大壩安全監控理論與地基工程監測研究。E-mail:wwgi555@163.com

2012-05-28 編輯:熊水斌)