應用灰色模型預測沈陽市沈河區乙肝流行趨勢
遼寧省沈陽市沈河區疾病預防控制中心(110014) 安震東
應用灰色模型預測沈陽市沈河區乙肝流行趨勢
遼寧省沈陽市沈河區疾病預防控制中心(110014) 安震東
目的 應用灰色模型預測沈陽市沈河區乙型病毒性肝炎(以下簡稱乙肝)發病流行趨勢,為乙肝防治提供科學依據。方法 采用中國疾病預防控制信息系統中沈陽市沈河區2006~2011年乙肝發病資料進行乙肝發病率研究,利用GM(1,1)模型外推預測2012年和2013年乙肝發病率趨勢。結果 2006-2011年沈河區乙肝發病呈下降趨勢,2012年和2013年乙肝發病估計值分別為11.8349/10萬和9.7071/10萬,預測精度為優。結論 灰色模型可應用于沈河區乙肝發病率趨勢預測,擬合效果理想。
乙型病毒性肝炎 灰色模型 預測 流行趨勢
乙型肝炎(以下簡稱乙肝)是由乙型肝炎病毒引起的,以肝臟為主要病變并可引起多種器官損害的一種傳染病。乙肝病程遷延,易轉變成慢性肝炎、肝硬化及肝癌〔1〕。為了解沈河區乙肝發病流行趨勢,本文應用灰色預測模型中的GM(1,1)模型對乙肝發病率進行分析和預測,從而建立乙肝等傳染病預警機制,為乙肝防治提供科學依據。
資料和方法
1.資料來源
數據來源于中國疾病預防控制信息系統中沈陽市沈河區2006-2011年乙肝發病資料。
2.方法
根據灰色系統理論建立GM(1,1)模型,應用EXCEL軟件實現灰色數列模型GM(1,1)的預測〔2〕。
(1)將2006-2011年沈河區乙肝發病率排列成動態數列Xt(t=0,1,…n),其中Xt表示t時刻的原始數據。
(2)累加數列和均值數列生成按照公式(1)、(2)分別求出一次累加數列Yt和均值數列Zt:
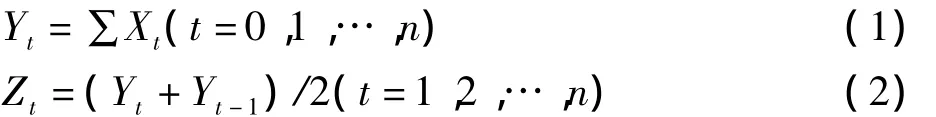
(3)建立 GM(1,1)模型
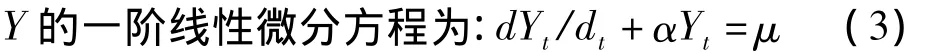
(3)式即為GM(1,1)模型,其中α、μ為待定系數。按微分方程的求解方法得到:
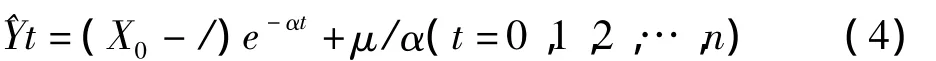
其中X。為初始時刻的原始數據,根據最小二乘法估計參數的:
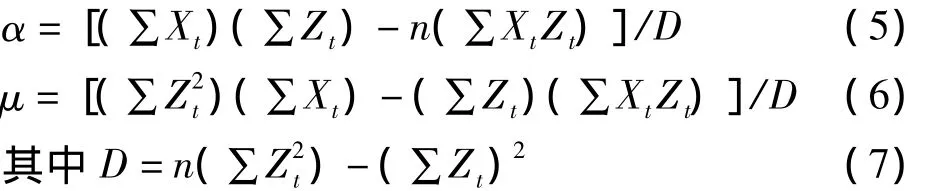
求預測值按公式(4)和(8)計算預測值:
(4)檢測預測模型精度:
①殘差檢驗
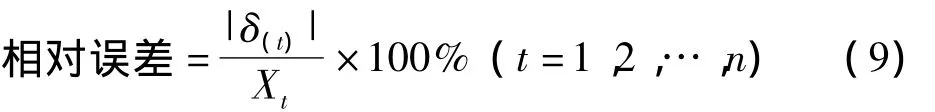
相對誤差小于20%稱模型為合格模型,則可用建立的模型進行預測。
②關聯度檢驗
關聯系數:
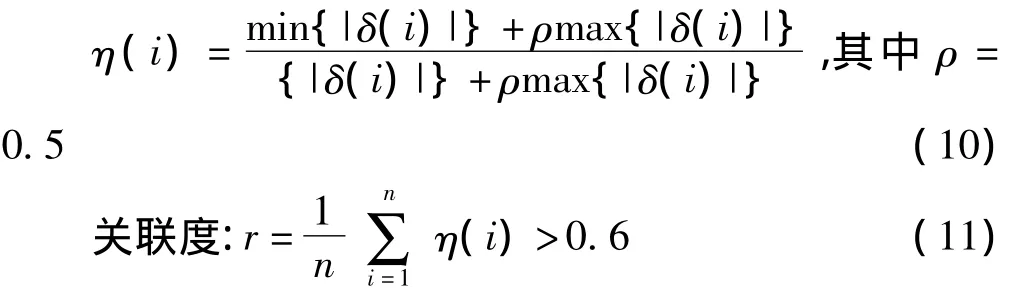
③應用后驗差檢驗
S1和S2分別為數列Xt和殘差δ的標準差:

3.外推判別
若C、P值計算結果符合表1中的判別要求,則利用下式進行外推預測。
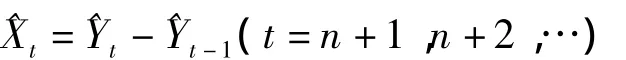
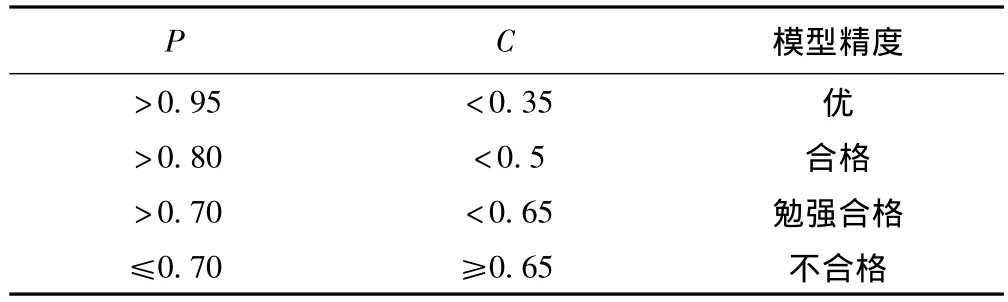
表1 后驗差檢驗判別參照表
結 果
1.乙肝的GM(1,1)模型擬合
將沈河區2006-2011年乙肝發病率數列在EXCEL軟件中進行統計分析得出模型參數分別為:α=0.1982,μ = 41.9838, 預 測 模 型 為:=-177.329e-0.1982t+211.8254。見表2。
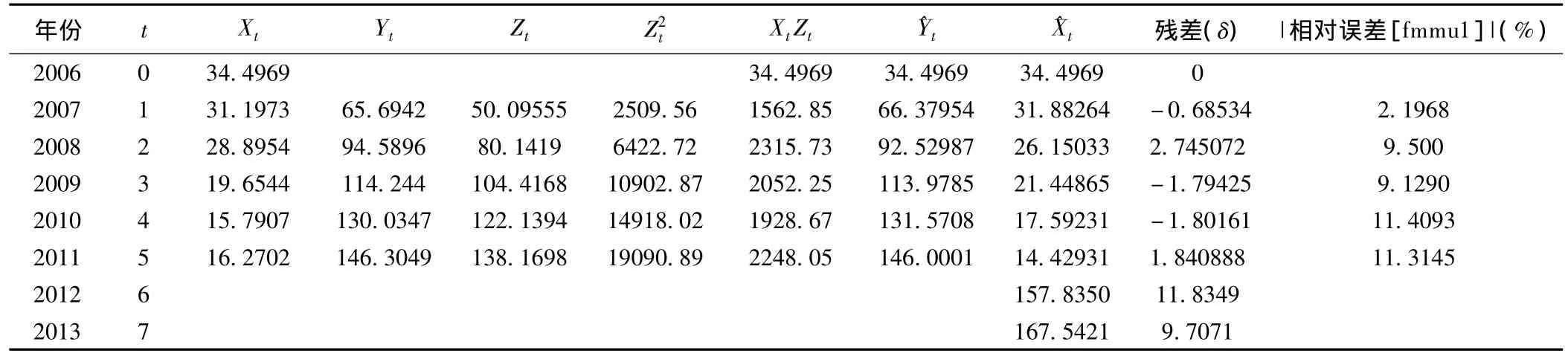
表2 沈陽市沈河區乙肝發病率(1/10萬)的GM(1,1)模型擬合結果及預測值
2.檢驗預測模型精度
(1)殘差檢驗
通過表2可以看出,相對誤差均小于20%,模型合格,因此可以建立模型。
(2)關聯度檢驗
根據式(10)及式(11)計算,關聯系數:η(i)={1,0.666967,0.333333,0.433416,0.432411,0.427126}
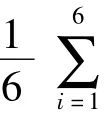
(3)后驗差檢驗
后驗差比值C是預測精確度檢驗的統計量,利用表2 中數據計算C=S2/Sl,S1=6.4556,S2=1.8889,C=0.2926,根據公式(15)算得=0.0610,0.6745Sl=4.354272,|δ-|<0.6745Sl的概率P=1.0>0.95,因此綜合判定GM(1,1)模型精度等級為優,擬合效果好,該模型可以用于乙肝發病率外推預測,見圖1。
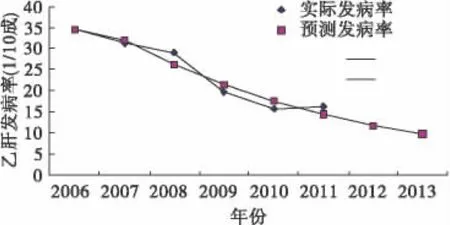
圖1 2006-2011年沈河區乙肝發病率GM(1,1)模型擬合圖
3.發病率外推預測
根據外推預測模型Yt=-177.329e-0.1982t+211.8254,外推2012年、2013年沈河區乙肝發病率分別為11.8349/10萬和9.7071/10萬。
討 論
灰色預測模型(gray forecast model)是通過時間序列的研究,尋找和發現事物發展變化的連續或離散的未來時間序列,從而分析事物發展變化的規律〔3,4〕。本文使用了應用最廣泛的 GM(1,1)預測模型,GM(1,1)模型是一種單變量一階線性模型,因其比多變量多階段模型計算簡單,對樣本含量和概率分布沒有嚴格要求,擬合度高,預測效果好,可以作為疾病監測和預測的有效工具〔5〕。本研究預測乙肝發病率模型的后驗差比值C<0.35,概率P>0.95,曲線擬合度理想,模型精度為優,因此外推是可信的,經過外推預測,沈河區今后兩年乙肝發病率呈現下降趨勢。
從預測結果看今后兩年我區乙肝發病率會逐年下降,但我們不應盲目樂觀,要想切實防治乙肝還需在做好患者管理的同時,還應對易感人群加以保護,開展多種形式的乙肝疫苗預防接種工作、加大乙肝防治宣傳、樹立防護觀念、做好血液制品管理、加強乙肝疾病監測等一系列預防控制措施。
1.迮文遠主編.計劃免疫學.第2版.上海:上海科學技術文獻出版社,2001:496.
2.韋麗琴,王素華,趙若望,等.應用EXCEL實現GM(1,1)模型對公路交通安全水平的預測.中國衛生統計,2004,21(6):345-346.
3.汪愛勤,魚敏.灰色預測方法在疾病預側中的應用.中華流行病學雜志,1988,9(1):49-52.
4.李秀央,李振洪,蔡雪霞.用EXCEL實現灰色數列模型GM(1,1)的預測.數理藥理學雜志,2000,13(4):296-297.
5.曲江文,劉建平,杜建偉,等.GM(1,1)灰色模型在瘧疾疫情預測中的應用.醫學與社會,2006,19(11):5 -7.
(責任編輯:劉 壯)

