局部特征尺度分解方法及其分量判據研究

楊 宇 曾 鳴 程軍圣

湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

0 引言

自適應時頻分析方法的特點主要表現在不需要對被分析信號的形態特征或者信息做出預測和限制的前提下，可以在對信號進行分解的過程中根據信號本身的特性自動產生基線信號，從而使得分解結果具有一定的物理意義。近年來最具代表性的自適應時頻分析方法是經驗模態分解（empirical mode decomposition，EMD）方法［1-2］，該方法在定義瞬時頻率具有物理意義的內稟模態函數（intrinsic mode function，IMF）分量的基礎上，通過上下極值點包絡線的平均來構造基線信號，從而將復雜的多分量信號自適應地分解為若干個IMF分量之和。由此可見，自適應時頻分析方法的關鍵在于基線信號的構造。

文獻［3］介紹了一種新的基線信號構造方法，即以原始信號任意兩個相鄰的極值點為跨度對信號進行分段線性變換來構造基線信號，且由此提出了內稟時間尺度分解（intrinsic time－scale decomposition，ITD）方法，并將其應用于腦電波癲癇信號的分析。ITD方法每次只經過單步迭代就得到固有旋轉分量（proper rotation component，PRC），即將基線信號從原始信號中分離后得到的剩余信號作為PRC分量，并將基線信號作為下一次迭代的原始信號，如此循環下去就可將信號分解為若干PRC分量之和。由于對于腦電波癲癇信號采用單步迭代分解就能得到有意義的分量，因此文獻［3］并沒有研究PRC分量的判據。

而對于一般的振動信號，單步迭代分解并不能保證分解出來的分量有意義，因此，本文在對ITD方法進行研究的基礎上提出了一種新的自適應時頻分析方法——局部特征尺度分解（local characteristic－scale decomposition，LCD）方法。該方法采用ITD方法中基線信號的構造方法，通過多次迭代自適應地將信號分解為若干個瞬時頻率具有物理意義的內稟尺度分量（intrinsic scale component，ISC）。LCD方法要分解出正確的ISC分量，首要的問題即為確定ISC分量的判據。對于ISC分量判據研究，可以參考EMD方法中一些主要的判據，如標準差判據［1］、S值判據［4］、三參數法［5］和能量差跟蹤法［6］等。本文將EMD方法中最常用的標準差判據應用于LCD方法，而標準差判據的閾值會因自適應時頻分析方法的不同而有所差異（EMD方法中標準差判據的閾值為0.2～0.3［1］），因此本文通過大量數據試驗確定適用于LCD方法的標準差判斷的閾值。對于不同的自適應時頻分析方法，標準差判據的適用閾值也不同，且在被應用之前都需要經過數據試驗以確定合理的閾值，并不具備自適應性。為了克服這一缺陷，本文在對瞬時頻率具有物理意義的典型信號的時域形態進行研究的基礎上提出了一種新的具有自適應性的分量判據——極值單調性判據，該判據無需設定任何閾值，僅僅依賴瞬時頻率具有物理意義分量的客觀存在的極值單調性。信號分析結果表明這兩種判據都可應用于LCD方法，而極值單調性判據具有自適應性，其適用性更強，能直接應用于EMD方法。此外，本文還對LCD方法和EMD方法的計算效率進行了對比分析，結果表明LCD方法在計算效率方面要優于EMD方法。

1 LCD方法

1.1 ITD方法基線信號的構造

ITD方法采用分段的形式對信號任意兩個相鄰的極值點之間的數據段進行線性變換而獲得基線信號。

設原始信號x（t）的極值為Xk（k＝1，2，…，M），其對應的時刻為τk（k＝1，2，…，M），如圖1中“·”所示。 由任意兩個極大（小）值點（τk，Xk）、（τk＋2，Xk＋2）連接形成的線段在其中間極小（大）值點（τk＋1，Xk＋1）對應時刻τk＋1的值為

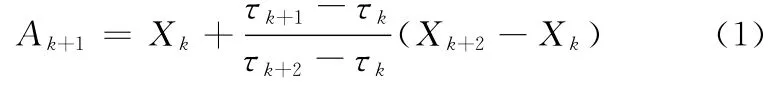
這樣可在點（τk＋1，Ak＋1）與（τk＋1，Xk＋1）之間用線性插值得到基線信號控制點（τk＋1，Lk＋1）的縱坐標值：

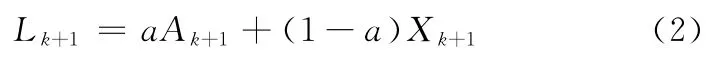
其中，a ∈ （0，1）為一常量，典型地，可取a＝1／2。圖1中“▲”所示即為基線信號控制點。

基線信號控制點對應的時刻τk（k＝1，2，…，M）將原始信號x（t）分割成若干個區間，在任意兩個相鄰極值點之間對x（t）進行線性變換：

圖1 ITD方法中基線信號的構造

1.2 LCD方法分解過程

LCD方法假設任何復雜信號由不同的ISC分量組成，任何兩個ISC分量之間相互獨立，這樣，一個多分量信號x（t）就可以被分解為有限個ISC分量之和，其中任何一個ISC分量滿足以下條件：①在整個數據段內，任意兩個相鄰極值點符號互異；②在整個數據段內，其極值點為Xk（k＝1，2，…，M），各個極值點對應的時刻為τk，由任意兩個極大（小）值點（τk，Xk）、（τk＋2，Xk＋2）連接形成的線段在其中間極小（大）值點（τk＋1，Xk＋1）對應時刻τk＋1的函數值Ak＋1與該極小（大）值Xk＋1的比值關系近似不變。

根據所定義的ISC分量，對信號x（t）進行LCD方法分解，可將其分解為若干個ISC分量之和，分解過程如下：

（1）確定原始信號x（t）的所有極值點（τk，Xk），利用式（1）～ 式（3）構造基線信號

（2）將m11（t）從原始信號中分離出來，得到剩余信號

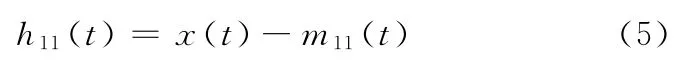
理想地，如果h11（t）滿足ISC分量判據，則h11（t）為信號x（t）的第一個分量ISC1（t）；如果h11（t）不滿足ISC分量判據，將h11（t）作為原始信號，重復步驟（1），則循環i次得到剩余信號h1i（t）＝h1i－1（t）－m1i（t），使得h1i（t）滿足ISC分量判據，h1i即為信號x（t）的第一個分量ISC1（t）。

（3）將ISC1（t）從原始信號中分離出來，得到

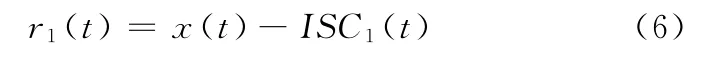
將r1（t）作為原始信號，重復步驟（1）、（2），得到x（t）的滿足ISC分量判據的第二個分量ISC2（t），重復循環n次，得到信號x（t）的n個滿足ISC分量判據的分量，直到rn（t）為一單調函數或者小于預設閾值為止。這樣便可以將x（t）分解為n個ISC分量和一個剩余函數rn（t）之和，即

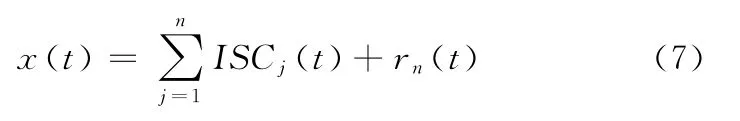
通過上述步驟，LCD方法可將一個多分量信號分解成若干ISC分量之和。與ITD方法相比，LCD方法在每次迭代過程中都對剩余信號進行分量判定，并通過多次迭代自適應地獲得ISC分量。

與EMD方法相比，LCD方法通過對原始信號本身進行分段線性變換來得到基線信號，而EMD方法的基線信號只是通過信號上下極值點包絡線的平均來獲取，并沒有充分用到原始信號數據，因此LCD方法中的基線信號能更有效地獲得原始信號的內在本質特征［3］。另外，LCD方法還避免了EMD方法采用三次樣條插值形成上下包絡線時可能產生的過包絡、欠包絡問題［7］。

1.3 仿真信號分析

考察如下所示仿真信號（采樣頻率2048Hz，t∈［0，1］s）：

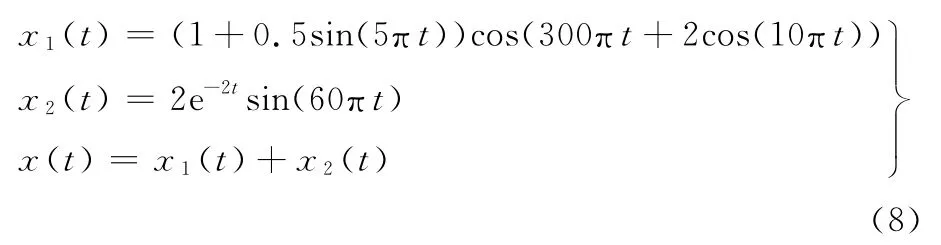
仿真信號x（t）由調幅調頻信號x1（t）和調幅信號x2（t）合成，其時域波形如圖2所示。

圖2 仿真信號x（t）的時域波形

對信號進行ITD方法分解，分解結果如圖3所示。由該分解結果可以明顯地看出，第一個分量PRC1是沒有意義的分量，它不能反映原始信號中的調幅調頻成分。對于一般的信號，ITD方法中單步迭代分解并不能保證分解出來的分量有意義，其使用范圍有限。

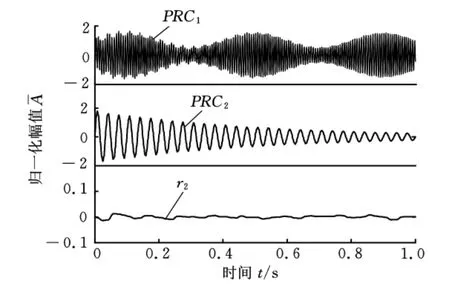
圖3 仿真信號的ITD方法分解結果

對信號進行LCD方法分解，初步設置單個分量迭代次數n＝6，分解結果如圖4所示。由該分解結果可以看出，分量ISC1和ISC2分別對應著原始信號中調幅調頻信號x1（t）和調幅信號x2（t），基本上能正確地反映出原始信號的成分特征。對比ITD方法，LCD方法的分解結果更準確。

圖4 仿真信號的LCD方法分解結果

2 分量判據研究

2.1 標準差判據

對于ISC分量判據研究，可以參考EMD方法中常用的標準差判據，即采用單個分量迭代過程中連續兩次迭代結果的標準差作為迭代終止條件［1］：

式中，T為信號長度。

當標準差SD達到某一給定閾值時則可認為迭代結束。為確定合理的標準差閾值，采用LCD方法對不同類型的仿真信號（如正弦、調幅、調頻以及調幅調頻等信號之間的相互疊加）進行分析。LCD方法首先將頻率相對較高的分量分離出來，因此可將獲取高頻分量的迭代過程作為研究對象，計算每次迭代的SD 值，并以均方誤差MSE作為分解效果的評價指標。下面僅給出由正弦和線性調頻疊加而成的仿真信號試驗數據。正弦和線性調頻疊加而成的仿真信號模型為

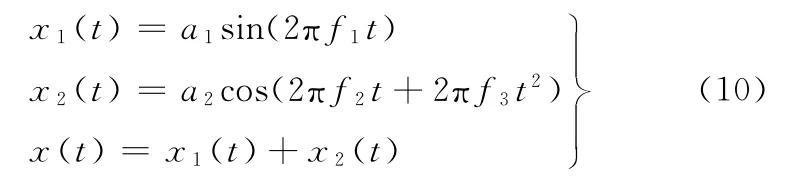
式中，a1、a2、f1、f2和f3均為模型參數。

改變模型參數得到6組參數：

分別在上述6組參數下各迭代10次得到的實驗數據如表1所示。觀察表1中數據，當各組參數下的SD 值分別滿足條件：①SD ＜0.012357612；②SD ＜ 0.046731089；③SD ＜0.158971762；④SD ＜ 0.430891421；⑤SD ＜0.172266713；⑥SD ＜0.018564477，則不同參數下的MSE相對來說都能夠取得較小值，因此對于式（10）所表示的仿真信號可取閾值SD ＜0.012357612。各類型仿真信號模型都有一個合適的標準差閾值使得在該模型不同參數下的MSE都能夠取得較小值，因此可取這些標準差閾值的交集作為LCD方法標準差判據的總閾值。

綜合各類型的仿真信號實驗數據，可以給出一個較為合理的標準差閾值：SD＜0.01。這個標準差閾值并不包括下限，一般說來，經過多次迭代得到較好分解效果時，當次迭代SD值已經很小了，接近于0（由表1也可以看出），因此沒有必要再設置SD的下限值。

2.2 極值單調性判據

極值單調性判據是本文提出的一種新的具有自適應性的分量判據。首先研究瞬時頻率具有物理意義的典型調幅調頻信號，其時域波形如圖5所示，給圖中極值點編序號。

表1 標準差判據研究中的部分實驗數據

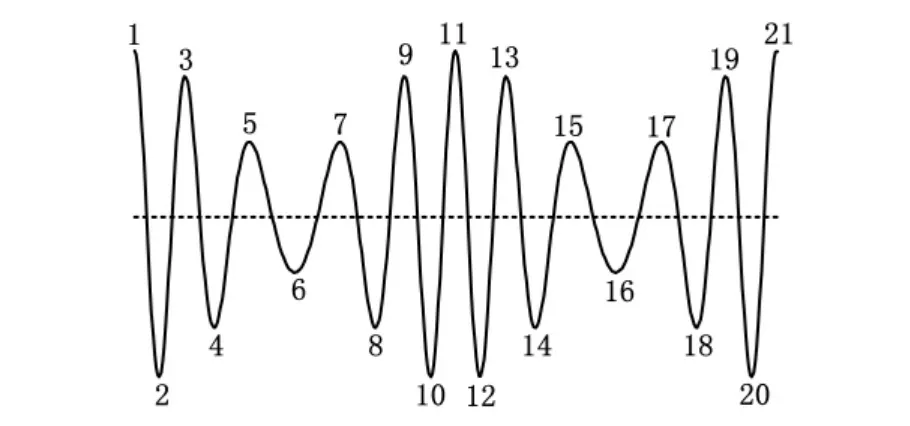
圖5 瞬時頻率具有物理意義的典型信號

將信號為負的部分取絕對值，如圖6中的虛線所示。觀察圖形可以發現，這些離散的極值點在時間尺度上不易發現其規律性，但它們在一定的極值點序列區間內存在單調性，如第6個至第11個極值點呈現單調遞增，第11個至第16個極值點呈現單調遞減，其中第11個極值點是極值點中的極大值點（可稱為二級極大值點），而第6和第16個極值點是極值點中的極小值點（可稱為二級極小值點）。這種離散的極值點序列所存在的單調性應當是瞬時頻率具有物理意義的分量的固有特性，利用這一特性可以近似進行分量判定，判定思路如下：

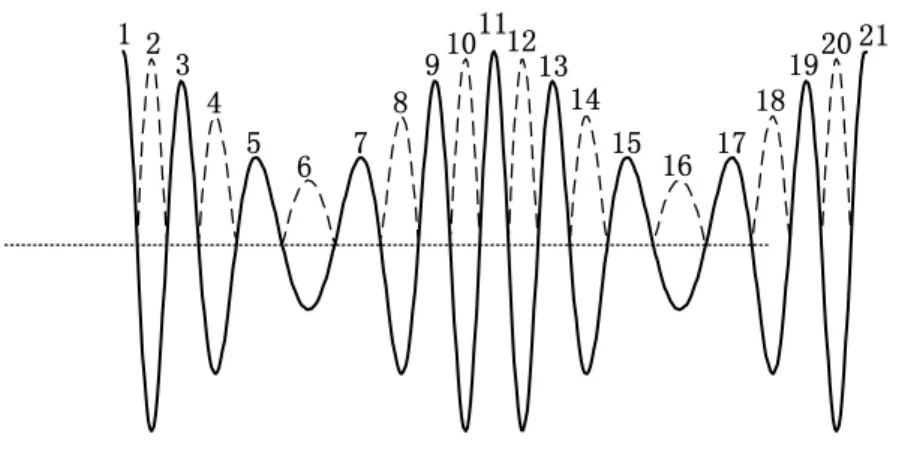
圖6 信號為負的部分取絕對值

（1）找出信號極大值點和極小值點，并保證極大值嚴格為正，極小值嚴格為負。

（2）確定由極大值點所產生的二級極值點，包括二級極大和極小值點。

（3）將二級極大值點與其前后相鄰兩個極值點（極大或者極小值點）進行絕對值大小比較，取三者中較大者作為新的二級極大值點，同理，將二級極小值點與其前后相鄰兩個極值點（極大或者極小值點）進行絕對值大小比較，取三者中較小者作為新的二級極小值點。

（4）對所有極小值點取絕對值，使得所有極值點序列均為正。

（5）找出由步驟（3）確定的相鄰兩個二級極值點分割所確定的極值點序列，并判斷這兩個相鄰的二級極值點的大小：①若前者小于后者，則該組極值點序列應當是單調遞增；②若前者大于后者，則該組極值點序列應當是單調遞減；③若兩者相等，則該組極值點序列應當是等值的。若信號滿足①、②和③中的一項，則可以認為該信號是瞬時頻率具有物理意義的分量。

現以圖5中調幅調頻信號為例說明極值單調性判定思路：

（1）極大值點已經嚴格為正，極小值點已經嚴格為負。

（2）若暫不對端點進行極值點定義，則正的極大值點所確定的二級極大值點為第11個極值點，二級極小值點分別為第5（或第7）和第15（或第17）個極值點。

（3）將第5個極值點（二級極小值點）與第4和第6個極值點進行絕對值大小比較，取絕對值較小的第6個極值點作為新的二級極小值點，同理可取第11個極值點作為新的二級極大值點，取第16個極值點作為新的二級極小值點。

（4）對信號為負的部分取絕對值使得極值點全為正。

（5）第6個極值點（二級極小值點）小于第11個極值點（二級極大值點），則該組極值點序列6、7、8、9、10和11應當是單調遞增，如圖6所示。其他極值點序列判定方法類似。

假設在上述步驟（5）中，第8個極值點大于第9個或者第10個極值點，即第6至第11個極值點區間內極值點序列不是單調遞增，那么在圖5中，我們可以直觀地感覺到該信號在第8個極值點附近不具有局部對稱性。

對于極值取絕對值后整個極值點序列呈單調性（如線性調幅信號）或者整個極值點序列保持為一個常值（如正弦信號）的信號，極值單調性判定方法依然適用。

極值單調性判據無需設定閾值，僅僅依賴瞬時頻率具有物理意義分量的客觀存在的極值單調性。滿足極值單調性判據的分量應該具有局部對稱性，其上下包絡平均應當接近零。

2.3 分量判據有效性驗證

2.3.1 仿真信號分析

為了驗證前面給出的標準差判據和極值單調性判據的有效性，考察如下所示仿真信號（采樣頻率2048Hz，t∈［0，1］s）：

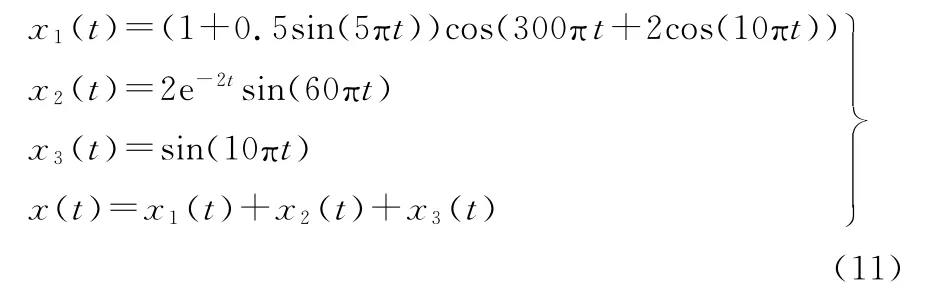
仿真信號x（t）由調幅調頻信號x1（t）、調幅信號x2（t）和正弦信號x3（t）合成，其時域波形如圖7所示。下面分別采用上述兩種分量判據對信號進行LCD方法分解。

圖7 仿真信號x（t）的時域波形

采用標準差判據對信號進行LCD方法分解，分解結果如圖8所示。采用極值單調性判據對信號進行LCD方法分解，分解結果如圖9所示。從理論上分析，調幅調頻信號x1（t）負的極小值點取絕對值后的所有極值點序列既存在單調遞增又存在單調遞減的序列區間；調幅信號x2（t）負的極小值點取絕對值后的整個極值點序列就是一個單調遞減的序列；正弦信號x3（t）負的極小值點取絕對值后的所有極值點序列是一個常值序列。

圖8 LCD方法分解結果（標準差判據）

圖9 LCD方法分解結果（極值單調性判據）

由分別采用標準差判據的LCD方法分解結果可以看出，分量ISC1、ISC2和ISC3都分別對應著原信號中調幅調頻信號x1（t）、調幅信號x2（t）和正弦信號x3（t），基本上能正確地反映出原始信號的成分特征，這表明了標準差判據（SD＜0.01）和極值單調性判據都可應用于LCD方法。

標準差判據是通過對大量但有限的各種類型仿真信號分解結果的分析而得到的，其閾值也會因自適應時頻分析方法的不同而發生變化；極值單調性判據是在對瞬時頻率具有物理意義分量的時域形態固有特性研究的基礎上得到的，且無需設定任何閾值，具有自適應性。因此，較之標準差判據，極值單調性判據的適用性更強。

現采用極值單調性判據對式（11）所示仿真信號進行EMD方法分解，分解結果如圖10所示。可以看出，EMD方法分解出來的各分量都能正確地反映出原始信號的各成分特征，這說明具有自適應性的極值單調性判據也能夠直接適用于EMD方法。

2.3.2 實驗信號分析

圖10 EMD方法分解結果（極值單調性判據）

實測的軸承為6311型滾動軸承，故障是通過在內圈上激光切割開槽來設置的，槽寬為0.15mm，槽深為0.13mm。振動加速度信號由安裝在軸承座上的加速度傳感器拾取。實驗裝置如圖11所示。

圖11 振動試驗裝置

圖12所示是測得的內圈有凹槽的滾動軸承振動加速度信號的時域波形，實驗時采樣頻率為4096Hz，軸轉頻為20Hz。經計算，滾動軸承內圈故障特征頻率為fi＝99.2Hz。

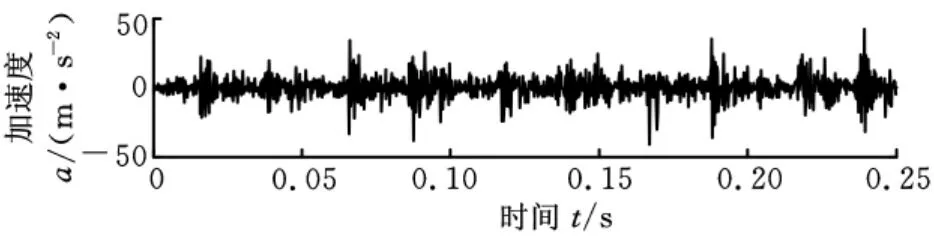
圖12 內圈故障滾動軸承振動加速度信號

限于篇幅，本文僅采用極值單調性判據對該實驗信號進行LCD方法分解。由于滾動軸承信號的故障信息主要集中在高頻段，因此只選取分解結果的前兩個ISC分量，如圖13所示。

圖13 LCD方法分解結果的前兩個分量

采用基于Hilbert變換的包絡解調方法分別對ISC1、ISC2進行解調，再進行包絡譜分析，得到譜圖，見圖14、圖15。可以看出，內圈故障特征頻率99.2Hz處都存在著明顯的譜線，由此可說明極值單調性判據的有效性。

圖14 ISC1的包絡譜圖

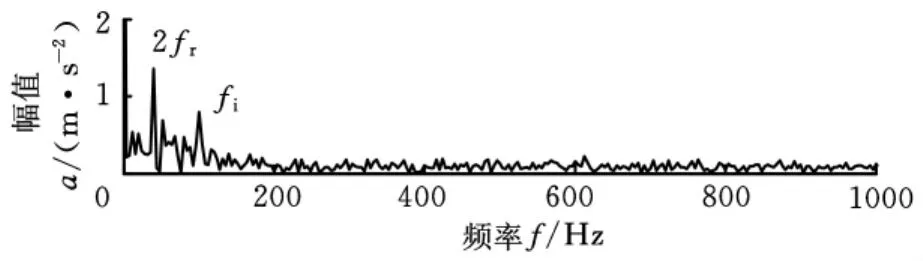
圖15 ISC2的包絡譜圖

3 LCD和EMD的對比分析

限于篇幅，本文僅從計算效率方面對LCD和EMD方法進行初步對比。由于標準差判據閾值會因自適應時頻分析方法算法的不同而變化，因此選擇適用性更強的極值單調性判據作為LCD和EMD方法分解的分量判據，分別對式（11）所示仿真信號進行分解。LCD和EMD方法分解的結果分別如圖9、圖10所示，其中各個分量的迭代次數以及分解所需的總時間如表2所示。

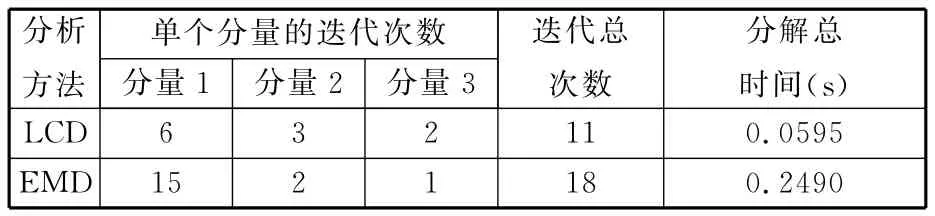
表2 LCD和EMD方法分解的迭代次數和分解總時間

由表2可看出，LCD方法的迭代總次數和分解總時間都要少于EMD方法。一方面，EMD方法的基線信號只是通過信號上下極值點包絡線的平均來獲取，并沒有充分利用原始信號數據，而LCD方法利用原始信號本身進行分段線性變換來得到基線信號，較之EMD方法能更加有效地獲取原始信號的內在本質特征，這就有利于減少迭代次數。另一方面，EMD方法中采用三次樣條插值計算基線信號，計算量較大，而LCD方法采用簡單的線性變換，避免了整體插值的過程，這樣計算量大大減少。綜合以上兩方面，LCD方法在計算效率方面要優于EMD方法。

4 結語

LCD方法是一種新的基于極值點的局部特征尺度參數的自適應、非平穩信號處理方法，該方法以信號任意兩個相鄰的極值點為跨度，并以分段的形式對信號進行線性變換來構造基線信號，從而通過多次迭代將信號自適應地分解為若干個ISC分量之和。本文在提出LCD方法的基礎上也在理論方面對其進行了初步探討，主要做了如下工作：

（1）將EMD方法中的標準差判據應用于LCD方法，并通過大量數據試驗確定適用于LCD方法的閾值，對仿真信號的分析結果表明這種判據可以應用于LCD方法。值得指出的是，對于不同的自適應時頻分析方法，標準差判據的適用閾值也不同，因此它不具備自適應性。

（2）在對瞬時頻率具有物理意義的典型信號的時域形態進行研究的基礎上提出了一種新的分量判據——極值單調性判據，仿真和實驗信號的分析結果驗證了該判據的有效性。較之標準差判據，極值單調性判據無需設定閾值，因此具有自適應性，其適用性更強，也可直接應用于EMD方法。

（3）對比分析了LCD和EMD方法的計算效率，對仿真信號的分析結果表明LCD方法在計算效率方面要優于EMD方法。LCD方法采用對原始信號進行簡單的分段線性變換獲取基線信號，迭代次數少，計算量小。

LCD方法的提出為自適應時頻分析方法提供了一條新的思路，但還有一些理論問題需要研究和完善，例如端點效應、模態混淆以及LCD方法適用的信號范圍等。隨著這些問題的深入研究，相信LCD方法能夠得到廣泛的應用。

［1］Huang N E，Shen Z，Long S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non－stationary Time Series Analysis［J］.Proceedings of the Royal Society，A，1998，454：903－995.

［2］Huang N E，Shen Z，Long S R.A New View of Nonlinear Water Waves：the Hilbert Spectrum［J］.Annu.Rev.Fluid Mech.，1999，31：417－457.

［3］Frei G M，Osorio I.Intrinsic Time－scale Decomposition：Time－freqeucny－energy Analysis and Real－time Filtering of Non－stationary Signals［J］.Proceedings of the Royal Society，A，2007，463：321－342.

［4］Huang N E，Wu M L C，Long S R，et al.A Confidence Iimit for the Empirical Mode Decomposition and Hilbert Spectral Analysis［J］.Proceedings of the Royal Society，A，2003，459：2317－2345.

［5］Rilling G，Flandrin P，Goncalves P.On EmpiricalMode Decomposition and Its Algorithms［C］／／IEEEEURASIP.Proceedings of IEEE－EURASIP Workshop on Nonlinear Signal and Image Processing（NSIP－03）.Grado，Italy：IEEE，2003：8－11.

［6］程軍圣，于德介，楊宇.經典模態分解方法中內稟模態函數判據問題研究［J］.中國機械工程，2004，15（20）：1861－1864.Cheng Junsheng，Yu Dejie，Yang Yu.Research on the Intrinsic Mode Function Criterion in EMD Method［J］.China Mechanical Engineering，2004，15（20）：1861－1864.

［7］Qin S R，Zhong Y M.A New Envelope Algorithm of Hilbert－ Huang Transform［J］.Mechanical Systems and Signal Processing，2006，20（8）：1941－1952.