氣體擠壓膜軸承的性能分析及其控制器的研究

朱達云 馬希直

南京航空航天大學，南京，210016

0 引言

基于超聲激勵的氣體擠壓膜現象已引起國內外許多學者的關注，氣體擠壓膜是在壓電激勵條件下的一種非線性效應，主要通過高頻振動不停地擠壓氣體，使氣體產生一定的壓力來克服物體的重力。目前已經研究出了各種不同的氣體擠壓膜機構［1-8］。1996年，Yoshiki［5］完成了彎曲波驅動下的氣體擠壓膜實驗，證實了超聲擠壓膜的承載能力。Shigeka等［6］和 Stolarski等［7-8］從20世紀90年代初開始研究氣體擠壓膜直線導軌，致力于研究具有實際作用的線型超聲擠壓膜軸承。1998年吉林大學壓電驅動研究室對超聲擠壓膜現象進行了系統的研究，初步解釋了超聲振動下氣體擠壓膜產生的原因［9］。

本文應用超聲激勵的氣體擠壓膜原理，設計了一種新型的氣體擠壓膜軸承。通過數值計算和有限元法分析計算了氣膜的厚度、氣膜壓力分布、軸承的振動模態和應力分布等，并為該軸承設計了一套控制器，在實驗中取得了較好的效果。

1 氣體擠壓膜軸承的結構和工作原理

本文提出的氣體軸承的結構如圖1所示，這個系統包括一個基于彈性鉸鏈的滑塊，一個直線導軌及壓電驅動陶瓷。軸承實物如圖2所示。

圖3是該滑動軸承的剖視圖。由于該軸承是軸對稱結構，所以在對其進行分析時，可取其一部分進行研究。單元A是提供高頻振蕩的部分，單元B是用來和光滑的導軌表面形成氣膜的部分。這兩個單元的彎曲振動是由3個彈性鉸鏈提供的。彈性鉸鏈的作用主要有兩個：一是使激振力均勻地分布在單元A上；二是當單元A有位移時，單元B能通過彈性鉸鏈的變形產生擠壓運動［10］。

圖1 擠壓膜軸承機構示意圖

圖2 軸承實物圖

圖3 軸承剖面圖

如圖4所示，當在壓電晶體上施加交變電壓使其工作在共振狀態時，壓電晶體能夠周期性地伸縮，產生高頻振動，使單元A產生一個振動，再通過彈性鉸鏈的作用，使單元B對氣隙中的氣體進行周期性的擠壓，從而形成氣體擠壓膜，并產生一定的承載能力。在工作過程中，軸承的四個面都將產生氣膜壓力，上部氣膜支承著整個軸承的重量，其他三個面上的氣膜起到穩定的作用，使滑塊不和導軌接觸，減小摩擦力，增加穩定性［11］。

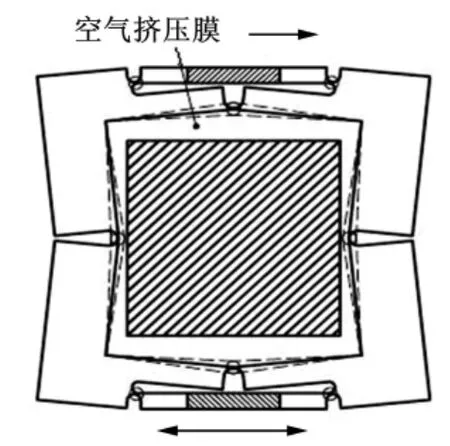
圖4 工作原理圖

2 應力狀態分析

由于該軸承特殊的工作方式，所以有必要對該軸承的應力狀況，特別是彈性鉸鏈附近的應力狀況進行分析。本軸承材料為鋁合金，屈服強度較高。以下是該材料的性能參數：密度2700kg／m3，彈性模量70GPa，泊松比0.33，屈服強度280MPa，軸承質量約為220g。

為了得到軸承在正常工作時的應力分布，本文采用有限元法，利用ANSYS軟件對軸承進行壓電耦合分析。用ANSYS進行仿真時，加在壓電陶瓷電極上面的電壓為400V。

從ANSYS分析的結果可以看出（圖5），最大的應力集中在彈性鉸鏈的附近，加400V電壓所產生的最大應力是6.73MPa，遠遠小于軸承的屈服強度，所以軸承能承受這樣的一個變形。同時，利用ANSYS對應力最大處進行疲勞分析，通過對應力最大的節點的分析，發現該節點的疲勞壽命為3.067×1011次，可近似看作是無窮次，最危險點的壽命是無窮次，說明該軸承不會發生疲勞破壞，滿足設計要求。

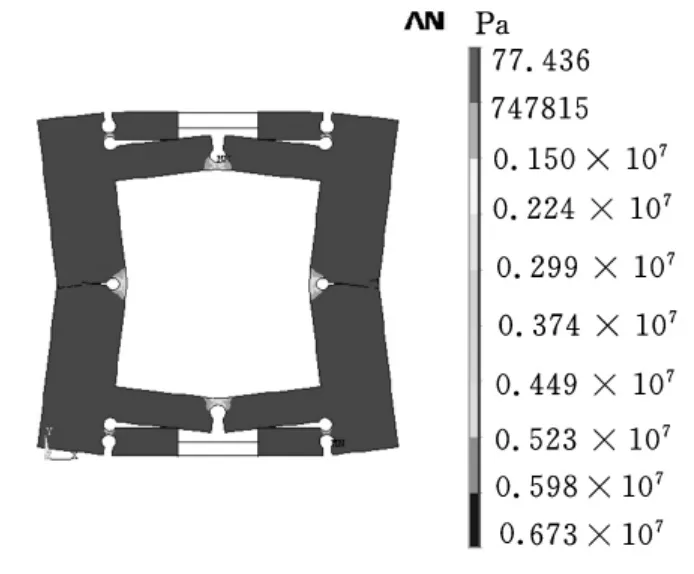
圖5 應力分布狀況

3 振動模態分析

為了獲得合適的激振振型來提高擠壓膜的壓力，首先對所設計的軸承進行模態分析，提取前三階模態，所獲得的三階振型如圖6所示。

圖6 軸承振動模態

由有限元分析得到該模型的三階諧振頻率為20 136Hz，在這個頻率下，軸承能獲得更大的變形，并能得到更大的氣膜厚度，從而增加該軸承的承載能力。同時，工作在諧振頻率下，可以用較低的電壓和能耗獲得同樣的氣膜厚度。

4 氣膜壓力分析

4.1 控制方程

根據軸承的變形情況，可以推導出該擠壓膜軸承的理論模型，如圖7所示。

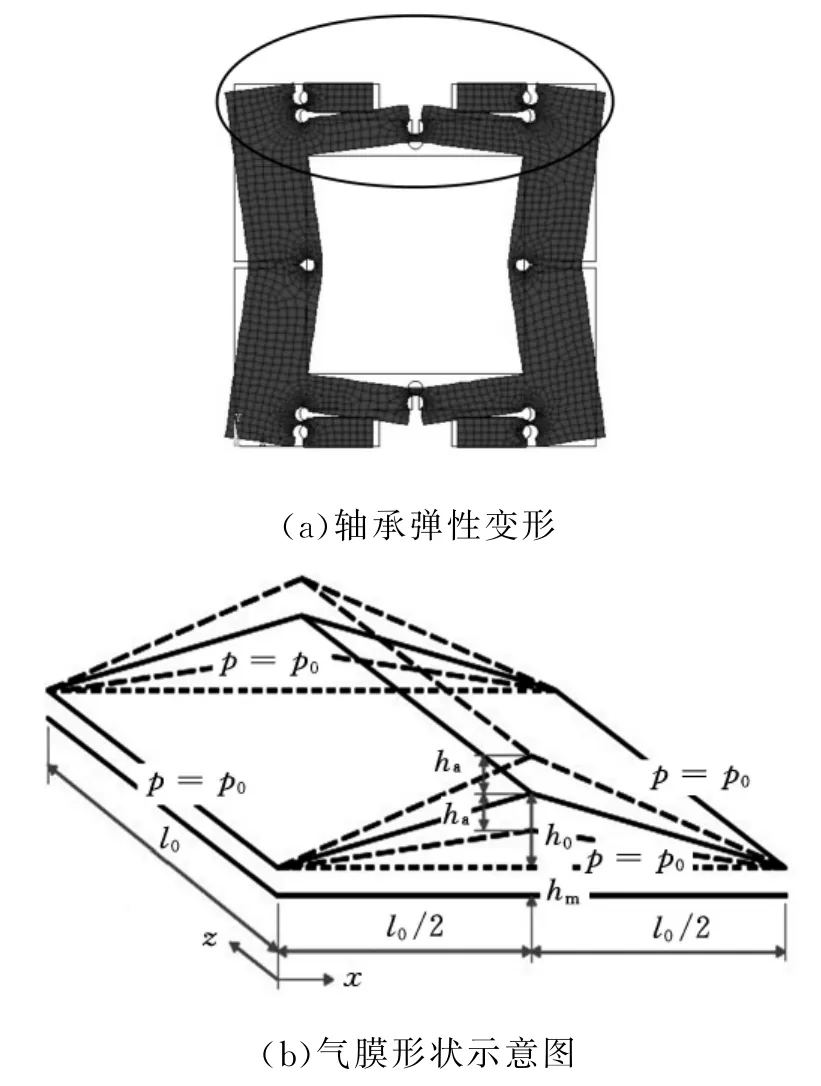
圖7 氣體擠壓膜軸承的理論模型

圖7是擠壓膜導軌正常工作時所產生的擠壓膜模型，可以看出這是一個2D矩形擠壓膜，可以應用2D矩形擠壓膜Reynolds方程進行求解。假設所形成矩形氣膜的邊長為l0，軸承和軌道之間的原始間隙為hm，施加預緊力的情況下間隙的最大值為h0，軸承正常工作時的振幅為ha。由流體動力潤滑理論和幾何知識，可以得到擠壓膜直線導軌的膜厚方程、運動方程和Reynolds方程。

（1）當0≤x ≤l0／2時，膜厚方程為

當l0／2≤x≤l0時，膜厚方程為

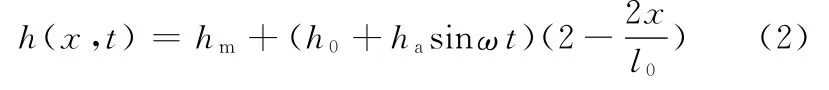
（2）運動方程為

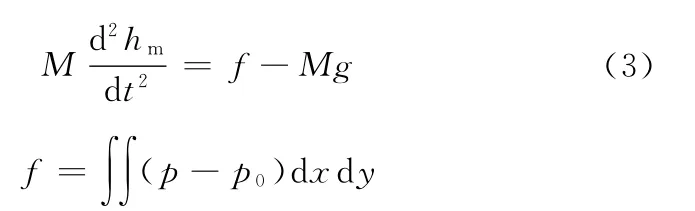
式中，g為重力加速度；M為滑塊質量；t為時間；p為氣膜壓力；p0為初始壓力。

（3）2D矩形擠壓膜Reynolds方程為

式中，μ為氣體的黏度；ρ為氣體的密度。

（4）邊界條件為：p｜x，y＝0＝p0；初始條件為：p｜t＝0＝p0，h｜t＝0＝hm。

可以用數值分析法，通過編寫Fortran程序對以上方程進行求解，計算出氣膜厚度和氣膜壓力分布［12］。在程序中分別設置電壓U 為50V、100V、150V、200V，頻率為5000～30000Hz，計算結果如圖8所示，從圖中可以看出，輸入電壓越大，氣膜厚度就越大。主要原因是因為輸入電壓增大，陶瓷的振幅就增大，同時軸承的變形也變大，對間隙氣體的擠壓幅度增加，使膜厚變大。

圖8 氣膜厚度理論計算值

設環境氣壓p＝1，則氣膜的平均壓力可以清晰地從圖9看出，第二時段時，負壓值最大為0.85，比環境壓力低了15%。在第四時段時，氣膜的正壓力達到最大值，約為環境壓力的1.41倍，比環境壓力高了0.41倍。所以，在整個工作過程中氣膜整體的正壓力大于負壓力，該氣體擠壓膜直線導軌具有一定的承載能力。

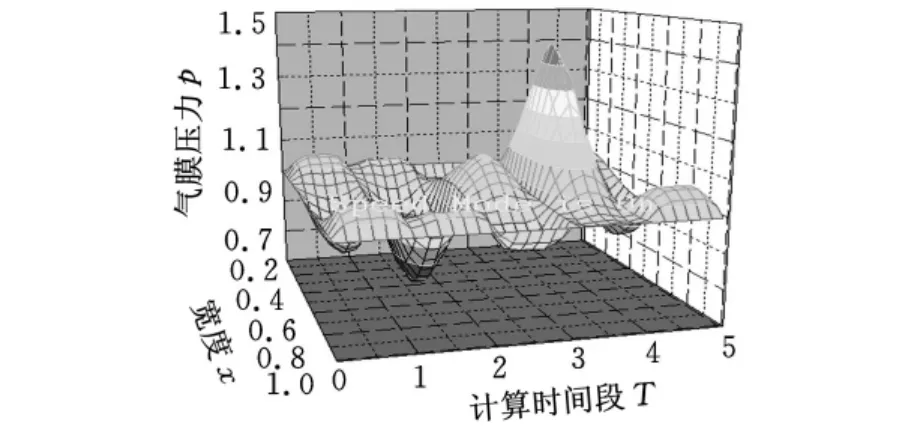
圖9 不同時段氣膜的平均壓力分布

4.2 有限元法分析氣膜壓力

本文對所設計的軸承的氣膜壓力分布采用ANSYS軟件，從聲學角度來進行仿真計算。使用ANSYS對該結構進行電－固－氣耦合的聲場分析，每個壓電片加載正弦電壓150V，通過設置載荷的頻率范圍，可以觀察到不同頻率下的近場聲壓分布。圖10所示是分別在5kHz、20kHz、50kHz頻率下的聲壓分布，最高聲壓分別是290Pa、3882Pa、561Pa。可以看出選擇在結構模態頻率處進行激振可以獲得較高的聲壓。以該彈性鉸鏈滑塊在20kHz頻率時所產生的近場聲壓分布，如圖10b所示，圖上顯示鉸鏈滑塊受到壓電陶瓷的伸展作用，處于被撐開的狀態，同時可以看出流體中聲波的指向性，以及聲場中的近場區、遠場區。

圖10 50kHz、20kHz、50kHz頻率下的聲壓分布

取圖10b中的中軸線上的聲場進行分析，繪制出中軸線上的聲壓情況，如圖11所示，可以看出軸線上聲壓的衰減情況。靠近聲源處的聲壓最大，隨著聲波傳輸距離的增大，聲壓減小。

圖11 20kHz頻率下軸承法線方向的聲壓變化曲線

利用ANSYS計算電－固－氣耦合情況下的聲場，從聲學角度解釋了氣體擠壓膜現象，仿真結果可以指導超聲懸浮的實驗設計，更好地選擇激振頻率與激振模態，并對實驗結果有預期的估計［13］。

5 控制器設計

根據壓電陶瓷振子的壓電效應原理，軸承工作時需要給壓電陶瓷振子輸入高頻交變電壓信號才能使其產生周期性的伸縮運動。由于該軸承沒有外部氣源，所以必須要設計一個控制器實時改變控制參數。由圖8可以看出，在一定頻率下，施加到壓電片上的電壓越大，所產生的氣膜厚度就越大，即氣膜壓力越大。所以控制器采用STC12C5410AD芯片，信號發生電路部分采用高速函數發生器MAX038，自動增益電路的運放采用數字控制的可變增益放大器AD8320。

帶超前校正環節的不完全微分PID控制器的傳遞函數的數學表達式為

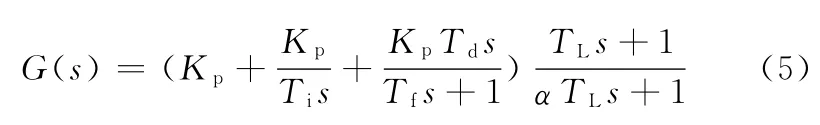
式中，Kp為比例系數；Ti為積分時間常數；Tf為濾波器系數為不完全微分環節為超前校正環節［14-15］。

6 系統實驗

由控制器、功率放大器、直線導軌、信號采集裝置組成的懸浮實驗臺如圖12所示。控制器產生的正弦信號被功率放大器放大后，施加在4塊壓電陶瓷上，使軸承產生具有承載能力的氣體擠壓膜。

圖12 實驗系統

圖13 軸承空載時的懸浮高度

給壓電陶瓷施加200V的激勵信號，使用激光位移傳感器對軸承的懸浮高度進行動態測量，結果如圖13所示，從圖中可以看出，在電壓從0連續調至200V的過程中，軸承的懸浮高度隨著電壓的增大而增大，并最終穩定在一定的范圍內，軸承的穩定懸浮高度為10～11μm。將質量為180g的砝碼加載到軸承上，將激勵信號電壓從0連續調節到200V，所測軸承懸浮高度如圖14所示，可以看出，有負載時的懸浮高度曲線走勢和空載時的走勢大致相同。當電壓調節到預設值后，軸承同樣處于穩定懸浮狀態，最終穩定在6.8μm左右。

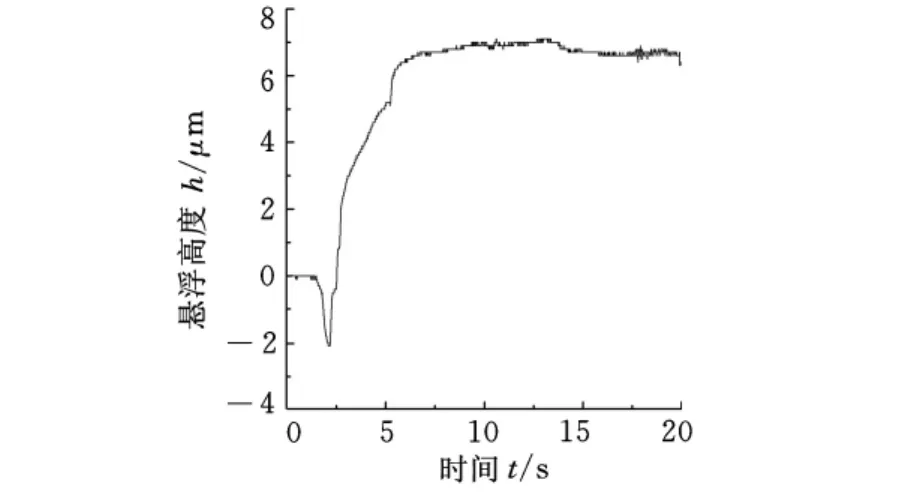
圖14 180g負載下的懸浮高度

7 結論

（1）運用非線性數值解法對2D矩形擠壓膜Reynolds方程和彈性變形進行了耦合求解，獲得了壓力分布、氣膜的厚度及氣模承載能力；并認為從聲學聲壓的角度也可對氣體擠壓膜壓力及承載能力進行分析。有限元疲勞強度分析結果認為處于高頻低幅振動狀態下的彈性鉸鏈疲勞強度能夠滿足設計要求。

（2）通過實驗測得在200V激勵信號驅動下，彈性鉸鏈氣體擠壓膜軸承空載以及載荷為180g時的懸浮高度，證明該軸承能夠穩定懸浮，并且具有一定的承載能力。

（3）實驗測試的懸浮高度低于理論計算值，主要原因是理論模型和實際軸承有一定的區別，如因軸承結構復雜導致的振動響應求解誤差，制造、安裝誤差以及零件的內應力等導致的形狀誤差等，以及實驗測量帶來的誤差，如殘留氣膜的影響、干擾信號以及環境振動等帶來的誤差。

［1］Salbu E O J.Compressible Squeeze Films and Squeeze Bearings［J］.ASME Journal of Basic Engineering，1964，86（3）：355－366.

［2］Minikes A，Bucher I.Coupled Dynamics of a Squeeze－film Levitated Mass and a Vibrating Piezoelectric Disc：Numerical Analysis and Experimental Study［J］.Journal of Sound and Vibration，2003，263：241－268.

［3］賈兵，陳超，趙淳生.基于近場超聲懸浮的耦合頻率特性分析［J］，中國機械工程，2011，22（17）：2088－2092.Jia Bing，Chen Chao，Zhao Chunsheng.Frequency Characteristics Based on Acoustic Near Film［J］.China Mechanical Engineering，2011，22（17）：2088－2092.

［4］黃明軍，周鐵英，巫慶華.超聲振動對摩擦力的影響［J］.聲學學報，2000，25（2）：115－119.Huang Mingjun，Zhou Tieying，Wu Qinghua.The Influence on FricationForce by Ultrasonic Vibration［J］.The Chinese Journal of Acoustics，2000，25（2）：115－119.

［5］Yoshiki H.Near Field Acoustic Levitation of Planar Specimens Using Flexural Vibration［J］.J.Acoust.Soc.，1996，100（4）：2057－2061.

［6］Shigeka Y，Hiroyuki K，Masaaki M.Float Characteristics of a Squeeze－film Air Bearing for a Linear Motion Guide Using Ultrasonic Vibration［J］.Tribology International，2007，40（3）：503－511.

［7］Stolarski T A.Load－carrying Capacity Generation in Squeeze Film Action［J］.International of Mechanical Sciences，2006，48（1）：736－741.

［8］Stolarski T A.Numerical Modeling and Experimental Verification of Compressible Squeeze Film Pressure［J］.Tribology International，2010，43：356－360.

［9］常穎，彭太江，闞君武，等.超聲振動對摩擦系數影響的試驗研究［J］.壓電與聲光，2003，25（6）：86－89.Chang Ying，Peng Taijiang，Kan Junwu，et al.Experiment Study on the Influence on Friction－factor by Ultrasonic Vibration［J］.Piezoelectrics and Acoustooptics，2003，25（6）：86－89.

［10］Stolarski T A，Wei Chai.Self－levitating Sliding Air Contact［J］.International Journal of Mechanical Sciences.2006，48（1）：601－620.

［11］常穎，吳伯達，程光明，等.超聲波軸承用壓電換能器模態分析及實驗研究［J］.哈爾濱工業大學學報，2006，38（5）：752－754.Chang Ying，Wu Boda，Cheng Guangming，et al.Model Analysis and Experiment Study on the Piezoelectric Transducer［J］.Journal of Harbin Institute of Technology，2006，38（5）：752－754.

［12］Stolarski T A，Woolliscroft S P.Performance of a Self－lifting Linear Air Contact［J］.Proc.IMechE，Part C：J.Mechanical Engineering Science，2007，221（5）：1103－1115.

［13］魏彬.超聲激勵的氣體擠壓膜線型導軌理論及實驗研究［D］.南京：南京航空航天大學，2009.

［14］陶永華.新型PID控制及其應用［M］.北京：機械工業出版社，2002.

［15］姜宏偉.基于TMS320F28335DSP的磁懸浮系統數字控制器研究［D］.南京：南京航空航天大學，2010.