含透鏡體的地質體真三維建模算法

李昌領，張 虹，朱良峰

（1.中國礦業大學 環境與測繪學院，江蘇 徐州221008；2.華東師范大學 地理信息科學教育部重點實驗室，上海200062）

0 引 言

目前，針對地層、地層中透鏡體的三維建模研究不太多見，針對二者整體統一建模的研究更加少見。Lamon［1］等采用B－reps模型對包含透鏡體、斷層等地質體進行了表面建模；程丹等［2］基于水文剖面圖設計了一種 “頂面—尖滅線—透鏡體”的三步建模方法構造透鏡體模型，對復雜地質體中透鏡體的建模進行了非常有益的探索。該算法側重于表面建模，還沒有考慮真三維實體的本質特征；其次把透鏡體從復雜地質體中 “分離出來”，單獨建模，乎略了周圍的地質環境，沒有考慮與地層或煤層的相依相伴關系。也有學者同時考慮了實體建模和地質體關系的問題，提出了虛擬鉆孔鏈的方法［3］，但人工刻意干預成份多，自動化程度不高。

本文在以上算法的基礎上，以表現地質體的三維實體性為目標，強調透鏡體和地層的整體統一建模，提出了“虛擬廣義三棱柱”的新模型，設計了一種基于該模型的真三維建模算法。

1 基本概念

定義虛擬廣義三棱柱。虛擬廣義三棱柱。使用GTP體元［4］對含透鏡體等特殊地質體建模時，在不增加虛擬鉆孔前提下，一個GTP體元中可能會出現二種或二種以上的不同地質體，若這些不同地質體的幾何形態、拓撲關系均能被該GTP體元準確的識別、表達，稱具有這些特性的GTP體元為虛擬廣義三棱柱體元 （virtual generalized triprism，VGTP），典型的VGTP體元如圖1所示。

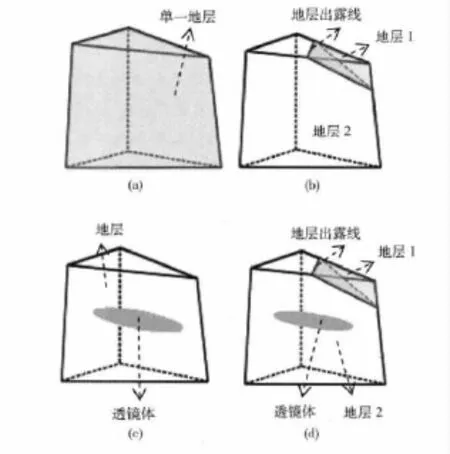
圖1 典型的虛擬廣義三棱柱VGTP體元

圖1（a）的VGTP中只含單一地層，它和普通的GTP沒有差別；圖1（b）的VGTP包含兩種地層，這是由于地層1的出露線位于VGTP頂面三角面內造成的；圖1（c）表示VGTP內部包含透鏡體 （或透鏡體的一部分），因而由地層和透鏡體兩種地質體構成；圖1（d）則是圖1（b）、（c）兩種情況的混合，同一個VGTP中包含了3種地質體。

由此可知，每個VGTP中可能包含二種或二種以上的不同地質體，具體到實體表示時，每個VGTP一次只能表達其中一種地質體，如圖1（c）中的VGTP，雖然其中包含兩種地質體，但只能二選一：用于表示普通地層時，VGTP代表了地層，用于表示透鏡體時，VGTP代表了透鏡體 （為簡單起見，用VGTP中包含透鏡體的多面體來表示透鏡體），圖1（b）中含有兩種地層，VGTP要么表示地層1，要么表示地層2。所以生成VGTP時應同時生成該VGTP的地質描述，即表示的是其中的哪一種地質體。

2 含透鏡體的地質體三維模型

包含或部分包含透鏡體的復雜地層三維模型如圖2所示。

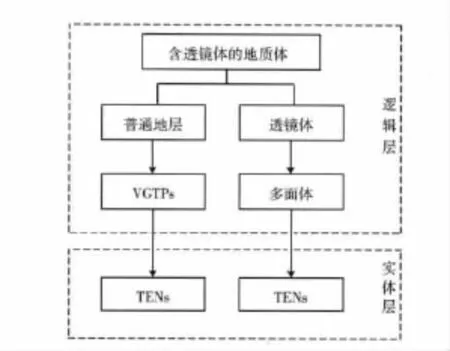
圖2 含透鏡體的地質體三維模型

從圖2中看出，含透鏡體的地質體作為一個整體，由地層和其中的透鏡體構成。普通地層由多個VGTP表達，每個VGTP幾何空間可能只表示單一地層，也可能因包含了透鏡體而只有部分空間表示地層。無論是VGTP的全部空間 （含單一地層）還是部分空間 （剔除了透鏡體后的剩余空間）最終會剖分成多個四面體 （tetrahedron，簡記為TEN），用多個TEN的整體來實現一個VGTP中的普通地層。透鏡體使用多面體模型表示，通過一定算法，也剖分成四面體TEN。TEN嚴格地表達了地質實體空間，非常適合于三維可視化、空間分析、空間統計、空間計算等。

VGTP和TEN是并存的，二者缺一不可，有VGTP就必然存在了相應的TEN，離開了TEN，VGTP便只有了概念上的意義，沒有實用性可言。透鏡體多面體和TEN也有同樣的關系。

TEN在模型中不是臨時存在的，而是整個模型不可分割的一部分。

3 建模算法

3.1 基本思想

總的來說，根據地層與透鏡體相依關系，考慮二者的整體建模。使用VGTP來描述普通地層，使用多面體模型來描述透鏡體，然后分別剖分成能夠精確表示這二種地質體的四面體。

具體來說，設定建模范圍，取得建模區域邊界面；生成透鏡體的三角網表面模型 （從實體角度來看，是一種多面體模型）；建立地層層序表，地層編號；加密鉆孔點；根據鉆孔數據生成地表Delaunay三角網 （D－TIN）；將D－TIN沿鉆孔跡線向下擴展生成地層的VGTP；若VGTP中包含或部分包含透鏡體，把 “含透鏡體”的信息寫入VGTP地質描述中。

根據VGTP地質描述，若VGTP中包含透鏡體，則按一定算法把透鏡體空間從VGTP空間中剔除，再把代表地層的剩余不規則空間剖分成四面體；若VGTP只包含單一地層，把整個VGTP空間剖分成四面體。

對于表示透鏡體的多面體，按一定算法也剖分成結構一致的四面體。

3.2 建模流程

建模流程如圖3所示。

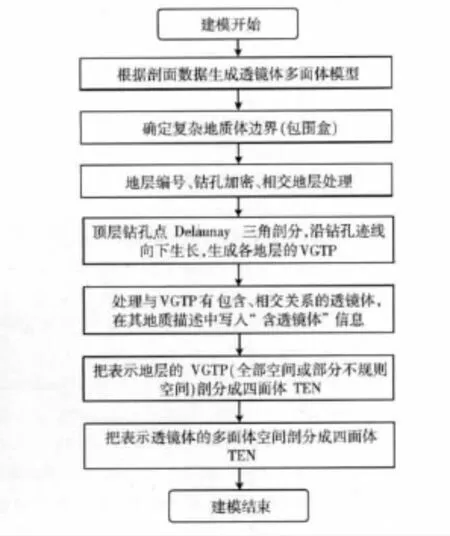
圖3 建模流程

3.3 透鏡體的多面體建模

根據程丹、楊欽等著文獻［2］中提出的方法，使用三角面構造透鏡體的表面，得到透鏡體的多面體模型。具體實現算法詳見相關文獻，這里不再贅述。

3.4 地層的邏輯層建模

地層層面編號［5－7］，鉆孔加密［8］，地層層面相交處理后，首先在最上層對鉆孔點進行Delaunay三角化［9］，形成Delaunay三角網，然后沿鉆孔跡線方向向下生成各地層的VGTP［10］。

生成VGTP過程中，若VGTP中包含或部分包含透鏡體，要把 “含透鏡體”信息、相關的透鏡體模型編號信息寫入VGTP地質描述中。

接下來還要做更精確的建模，即把VGTP中地層所占空間、透鏡體多面體分別剖分成四面體。

3.5 VGTP的四面體剖分算法

VGTP的四面體剖分算法是要剔除其中的透鏡體空間，再把剩下空間剖分成四面體。本文算法兩步合并，一次性完成四面體的剖分。

3.5.1 基本約定

四面體的每個三角面的法線方向為垂直于三角面指向四面體內部的方向；沿三角面法線方向看過去 （向四面體的內部看），每個三角面的頂點按順時針排列。

3.5.2 構成四面體的第四點的選點原則

已知一個三角面及其法向量，和位于法線一側的若干候選空間點，需從中選擇一點作為構成四面體的第四點，相對于三角面而言，選擇第四點的原則是：計算過空間點和三角面的外接球球心 （四面體外心），與三角面距離最小的外心對應的空間點就是最佳第四點。

3.5.3 剖分算法

對于地層模型中的每個VGTP，在不增加額外點或增加少數中間點 （由于出現了Schnhardt Polyhedron［11］情況，導致該類多面體不能直接被四面體化）的情況下，把其內部表示的地層空間剖分成四面體的算法如下：

若VGTP中只包含單一地層，則把整個VGTP看作一個多面體，使用Shewchuk的gift－wrapping算法［12］或切角算法［13］剖分成四面體。

若VGTP包含透鏡體或與透鏡體有相交關系，用VGTP的邊界面裁減掉位于VGTP外面的透鏡體。此時，地層模型抽象成這樣的幾何模型：VGTP面構成外環面、內部透鏡體表面構成若干內環面的含內孔的多面體，。

在文獻 Ghadyani的 LAST RESORT算法［14］和Shewchuk的gift－wrapping算法的基礎上，提出了一種空間約束域直接Delaunay四面體生長算法，在不增加額外頂點（或增加少量額外頂點）的前提下，以外環面和內環面為約束邊界面條件，一次性地把其中的不規則地層空間生長為四面體。剖分算法描述如下：

（1）初始化一個用于存放三角面信息的隊列；

（2）從外環面中任選一個三角面；

（3）根據3.5.2節選點原則，從該三角面處直接可見且位于該三角面法線一側的內、外環面上的所有頂點中，選擇一個最優的點，組成一個四面體，加入結果集；新生成的3個三角面的反面加入隊列；

（4）若隊列為空，則轉 （7），否則從隊列中移出一個三角面；

（5）對于新移出的三角面，從兩方面找出構成四面體的第四點的所有候選鄰接點。①若該三角面有一條邊位于外環面 （或內環面）上，則該三角面所在的外環面 （或內環面）上的候選點只有一個，即含該邊的三角形中與該邊相對的頂點 （還有一個頂點，但已構成了四面體）；②若該三角面只有一點位于外環面 （或內環面）上，則找出該點的所有鄰接點，再把位于該三角面的法線反向一側的鄰接點去除，剩下的鄰接點就是候選空間點；

（6）根據3.5.2節選點原則，從以上候選空間點中找出一個最優的點與該三角面形成一個新的四面體，加入結果集；新生成的三角面的反面進入隊列；轉第 （4）步；

（7）四面體剖分完畢。

算法執行完畢，若還有少量空間沒有剖分成四面體，應加入少量中間點、中間三角面，重新執行 （4）～ （7），直至多面體空間全部剖分成四面體。

3.6 透鏡體模型的四面體剖分算法

透鏡體模型是多面體模型，可以任選以下兩種算法剖分成四面體：Shewchuk的gift－wrapping算法、切角算法。

4 實驗結果

參照了開灤精煤股份有限公司某礦業分公司的地質數據，設計了一個地層模型，內部包含了兩個不規則的透鏡體，頂點數為518，初始邊界面數為1024。使用本文算法對其進行了約束Delaunay四面體剖分，結果如圖4所示。

圖4 含兩個透鏡體地層約束Delaunay四面體剖分結果

5 結束語

以往算法把透鏡體從復雜地質體中 “分離出來”單獨建模，忽略了其所在地層。本文充分考慮二者的相依關系，進行整體全面建模。其次，在以往面模型的基礎上，考慮地質體真三維實體的本質，以體元模型進行三維實體建模。在使用VGTP建模時，克服了GTP無法同時跨越地層和透鏡體的問題。最后，算法不需交互加入位于地層與透鏡體交界上的虛擬鉆孔點鏈，從而減少手工干預，增強了算法的自動化程度。本算法初步應用于研究區含透鏡體的復雜地質建模，取得了令人滿意的結果。

［1］Lamon A M，Jones NL.Building solid models from boreholes and user－defined cross－section ［J］.Computer and Geosciences，2003，29 （3）：547－555.

［2］CHENG Dan， YANG Qin. Three－dimensional geological modeling based on hydro sections ［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33 （11）：1362－1366 （in Chinese）. ［程丹，楊欽.基于水文剖面的三維地質建模方法 ［J］.北京航空天大學學報，2007，33 （11）：1362－1366.］

［3］LUO Zhiyong.Research and development of 3Dvisualization system for geological surveys ［D］.Chengdu：Chengdu University of Technology，2008 （in Chinese）. ［羅智勇.面向地質勘查的三維可視化系統研制與開發 ［D］.成都：成都理工大學，2008.］

［4］WU Lixin.Topological relations embodied in a generalized triprism （GTP）model for a 3Dgeoscience modeling system ［J］.Computers and Geosciences，2004，30 （4）：405－418.

［5］LUO Zhiyong，YANG Wunian.3Dmodeling and visualization of geological bodies based on borehole dada ［J］.Science of Surveying and Mapping，2008，33 （2）：130－132 （in Chinese）.［羅智勇，楊武年.基于鉆孔數據的三維地質建模與可視化研究 ［J］.測繪科學，2008，33 （2）：130－132.］

［6］XIA Yanhua，BAI Shiwei.Study of preprocessing of drilling data for building 3Dstrata model ［J］.Rock and Soil Mechanics，2012，33 （4）：1223－1226 （in Chinese）. ［夏艷華，白世偉.三維地層建模鉆孔數據預處理研究 ［J］.巖土力學，2012，33 （4）：1223－1226.］

［7］MING Jing.Quick construction and update of three－dimensional geological models based on boreholes ［J］.Geography and Geo－Information Science，2012，28 （5）：55－60 （in Chinese）. ［明鏡.基于鉆孔的三維地質模型快速構建及更新 ［J］.地理與地理信息科學，2012，28 （5）：55－60.］

［8］ZHU Liangfeng，PAN Xin，WU Xincai，et al.Construction method and actualizing techniques of 3Dvisual model for geological faults ［J］.Journal of Software，2008，19 （8）：2004－2017（in Chinese）.［朱良峰，潘信，吳信才，等.地質斷層三維可視化模型的構建方法與實現技術 ［J］.軟件學報，2008，19 （8）：2004－2017.］

［9］SHI Wenzhong，WU Lixin，LI Qingquan，et al.Models and algorithms for three dimensional spatial information system ［M］.Beijing：Publishing House of Electronics Industry，2007：50－58 （in Chinese）.［史文中，吳立新，李清泉，等.三維空間信息系統模型與算法 ［M］.北京：電子工業出版社，2007：50－58.］

［10］HU Gang.Research of 3Dvisualization of geologic body based on borehole data ［J］.Geomatics World，2012 （2）：64－69（in Chinese）.［胡剛.基于鉆井數據的地質體3維可視化研究 ［J］.地理信息世界，2012 （2）：64－69.］

［11］Edward Verbree.Piecewise linear complex representation through conforming delaunay tetrahedronization ［C］／／Proceedings of 4th International Conference on Geographic Information Science.New York：Springer，2006：385－387.

［12］Shewchuk J R.Constrained delaunay tetrahedralizations and provably good boundary recovery ［C］／／Proceedings of 11th International Meshing Roundtable.New York：Springer，2002：193－204.

［13］LI Changling，ZHANG Hong，ZHU Liangfeng.Improved algorithm for dividing an arbitrary polyhedron into tetrahedrons ［J］.Computer Engineering and Applications，2012，48（25）：20－23 （in Chinese）.［李昌領，張虹，朱良峰.一種任意多面體剖分成四面體的改進算法 ［J］.計算機工程與應用，2012，48 （25）：20－23.］

［14］Ghadyani H，Sullivan J，WU Ziji.Boundary recovery for delaunay tetrahedral meshes using local topological transformations ［J］.Finite Elements in Analysis and Design，2010，46（1－2）：74－83.