葉枝分辨的決策樹研究

劉 軍

（南京工業大學 電子與信息工程學院，江蘇 南京210009）

0 引 言

當前基于單劃分屬性建立決策樹算法主要存在以下問題：基于信息增益的算法是一種局部優化策略［1－2］，當屬性集中多個屬性的信息增益相近時難以準確地確定出劃分屬性，且指數運算復雜度高；基于粗糙集［3］的決策樹生成算法要經過屬性約簡和確定劃分屬性兩個步驟［4－5］，屬性約簡存在多選性及難以準確保留有效屬性的問題［6］，而且單以核屬性強度確定劃分屬性并不能獲得最佳效果，因為決策樹優化是個全局問題，當前屬性集中分辨最強的單個屬性可能只是本集局部最優而非全局最優。如果要達到全局最優需要進行大量的預測計算，顯然上述算法難以實現。為此提出了一種基于粒計算［7］的精準建樹算法，該算法不僅考慮當前層中屬性的分辨能力，而且預測其后續層中的分辨趨勢。根據粒計算［7］理論，將每個屬性按屬性值劃分為葉 （基本粒），每個條件屬性葉對應的決策屬性葉的種類個數稱為枝，用這兩個參數測定該條件屬性粒的分辨力。條件屬性的分辨力則由其各基本粒分辨力之和所決定，分辨力最高者為劃分屬性。由于粒計算的簡潔性，對分辨力相近屬性可以再計算比較其后續層的分辨力，最終得到最佳劃分屬性，這是一種全局判優的算法。另外，采用數據庫SQL語言查詢可以降低計算復雜度。由大量實例比較分析可知，該算法計算量較小且準確度較高。

1 理論及實現

1.1 理 論

決策表［7］S＝（U， ｛An｝，D，V）， ｛An｝為條件屬性集，D為決策屬性，U＝｛x1，x2，…，xm｝是論域，V是屬性值集。

定義1 條件屬性Ai中各取值相同部分為一個基本粒［7－8］，記為 （Ai，v）， ｛（Ai，v）｜Ai∈｛An｝，v∈V）｝。基本粒中相同值的記錄數量稱為粒值量 （葉重量），記為WAi（v），WAi（v）＝｛Count（xi∈U）｜（Ai，v）｝。Ai中包括基本粒的數量稱為該屬性的粒數量，記為N（Ai）。N（Ai）表示Ai可劃分為幾種葉子Ai（v）；而 WAi（v）表示一種葉子一次可分配的重量。

定義2 決策屬性D中各取值相同部分也為一個基本粒，記為 （D，u），｛（D，u）｜u∈V｝。在決策表S的｛xi∈U｜（Ai，v）｝行集中存在的 （D，u）數量稱為枝數量，記為SD（u），｛SD（u）＝ClassCount （xi∈U｜（Ai，v），u∈D）｝。SD（u）表示在 （Ai，v）約束的行集中，可接受WAi（v）分配的枝數量。

若干個基本粒（Ai，v）組成屬性Ai，所以每個（Ai，v）對應于（D，u）的關系決定（Ai，v）分辨能力，Ai中所有（Ai，v）的分辨能力與N（Ai）又共同決定Ai的分辨能力，這就是葉枝粒比算法的主要理論依據。

例如在表2中，屬性 A3中有5個基本粒（Ai，v）：（A3，3）、（A3，4）、（A3，5）、（A3，6）、（A3，8），N（A3）＝5。5個基本粒對應 WAi（v）分別是：｛WA3（3）＝2｜（U＝3，8）｝，｛WA3（4）＝1｜（U＝7）｝，｛WA3（5）＝3｜（U＝5，6，10）｝，｛WA3（6）＝2｜（U＝1，4）｝，｛WA3（8）＝2｜（U＝2，9）｝。

WA3（3）對應的行集（U＝6，8）中D有1種粒（D＝2），所以其SD（2）＝1

WA3（4）對應的行集（U＝7）中D有1種粒（D＝1），所以其SD（1）＝1

WA3（5）對應的行集（U＝5，6）中D有2種粒（D＝4、3），所以其SD（4，3）＝2

WA3（6）對應的行集（U＝1，4）中D有2種粒（D＝5、1），所以其SD（5，1）＝2

WA3（8）對應的行集（U＝2，9）中D有1種粒（D＝3），所以其SD（3）＝1

1.2 實 現

最優樹的標準是樹葉（重量）大且樹枝少，具體到基本粒（Ai，v）時，因為 WAi（v）是可分配的葉重量，而SD（u）是接受分配的枝個數，所以最優數應是WAi（v）值大且SD（u）小；具體到 Ai時，則是∑（WAi（v）／SD（u））大且 N（Ai）小。當（Ai，v）的分辨力確定后，Ai中各（Ai，v）的分辨力累加和即為Ai的分辨力，而｛An｝中分辨力最大者確定為劃分屬性。

WAi（v）和SD（u）兩個參數決定了（Ai，v）的分辨能力，依據 WAi（v）和SD（u）可以推導出判別（Ai，v）分辨能力的一般式：若SD（u）＝1，經結點劃分，（Ai，v）一次分辨出u∈D中的WAi（v）行，得葉結點1個，該葉的平均重量為WAi（v）／SD（u）＝WAi（v）／1＝WAi（v），枝個數為SD（u）＝1；若SD（u）＝2，一次結點劃分后只得2個分區，至少要經二次結點劃分得2個葉結點，平均葉重量為 WAi（v）／SD（u）＝WAi（v）／2，枝個數為 SD（u）（＝2）；依此，得（Ai，v）的平均葉重量及枝個數的一般式

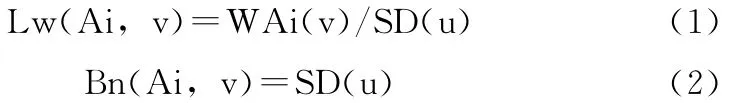
為了判定按（Ai，v）劃分后其后續層的分辨力，在｛xi∈U｜（Ai，v）｝所組成的行集中判出分辨力最強者代表（Ai，v）極大分辨力，即在｛xi∈U｜（Ai，v）｝行集中判出最優列。由于每列又由若干子粒組成（設共有m列），每列的葉枝量是其各子粒葉枝量之累加和：

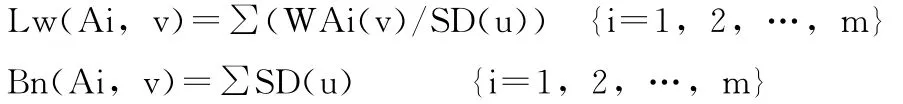
而（Ai，v）的極大分辨力定為：

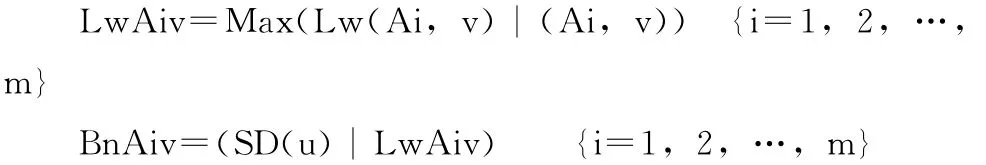
屬性Ai∈｛An｝極大分辨力為其各基本粒之累加和：

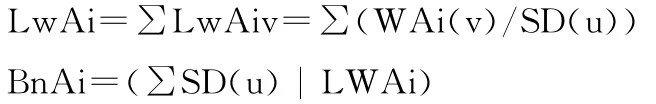
屬性Ai的分辨力由LwAi和BnAi及N（Ai）共同確定，其平均極大粒比為：

在｛An｝屬性中平均極大葉枝粒比最大者即為劃分屬性：

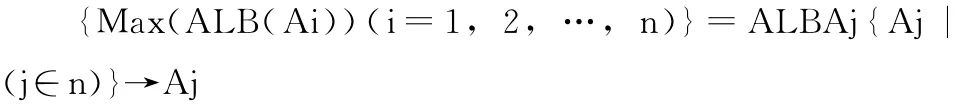
當有多個Aj時（分辨力接近），則要根據樹的層次上N（Ai）被分辨情況再次對多個Aj進行分辨（見2.2）。經Aj劃分后得1個樹結點，在Aj的各劃分集中再按上述算法逐層進行擇優，可得葉枝粒比最大，分辨力最強的決策樹。

2 比較實例

2.1 與ID3［9－10］改進算法的比較

將文獻［11］表1經等價標準化后見表1，對屬性A1（Topic）共包括3個粒：（A1，2），（A1，3），（A1，4）。其中（A1，2）的劃分集為 U＝｛6，8，12，13，18，19，22｝，被排序至表1的前7行，記為S（A1，2）。

在S（A1，2）中對A1列：

WA1（2）／SD（1，2）＝7／2＝3.5；SD（1，2）＝2；記為（3.5，2）。

對A2列：

∑（WA2（1，2，3）／SD（1，2））＝WA2（1）／SD（1）＋WA2（2）／SD（2）＋WA2（3）／SD（2）＝3／1＋2／1＋2／1＝7；

∑SD（1，2）＝1＋1＋1＝3；記為（7，3）。

同理可得，A3列：（5.5，4）；A4列：（5，5）；A5列：（4.5，4）；A6列：（4，5）。

表1 標準化后的決策數據

通過上述比較可得最優列為A2列，即選其為（A1，2）的有效葉、枝量（Lw（A1，2）＝7，Bn（A1，2）＝3）。

類似地可得A1其它粒優選后的有效葉、枝量：（Lw（A1，3）＝7，Bn（A1，3）＝5）；

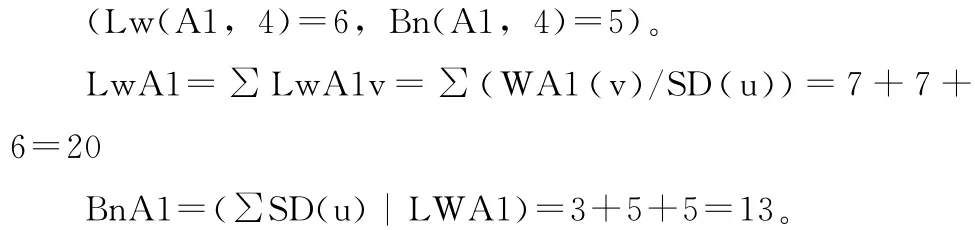
則A1平均極大葉枝粒比為ALB（A1）＝20／13＝1.5

類似上述過程得A2、A3、A4、A5和A6的平均極大葉枝粒比分別為：

所以 Max（ALB（Ai））（1，2，3，4，5，6）＝ALB（A1）

屬性按上述葉枝粒比，優選屬性順序為：A1、A2、A3、A4、A5、A6。

首選A1為劃分屬性，逐級擇優劃分為決策樹：

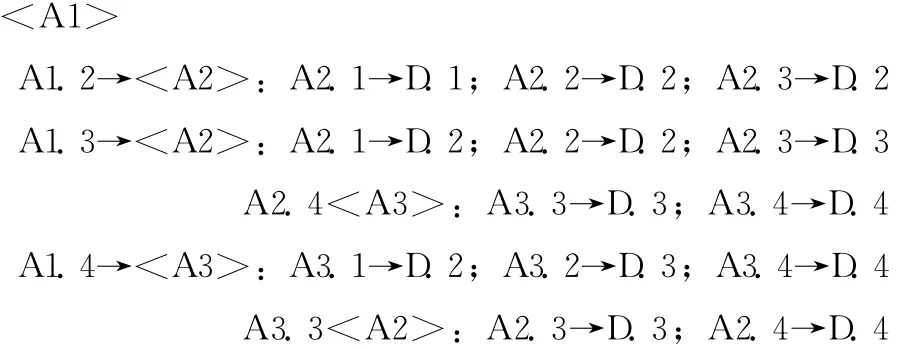
此樹共有18個枝（是文獻［11］表1的最優決策樹）。而首選A2劃分則為20個枝；首選A3劃分則為22個枝；首選A4劃分則為25個枝；首選A5劃分則為25個枝（深度比A4多一層）；首選A6劃分則為26個枝，完全符合上述葉枝粒比的排優順序。文獻［11］中圖1所示是以A2（view and arguments）為首選劃分屬性建樹，比首選a（Topic）建樹多了2個樹枝，所以并非最優樹。

2.2 與 C4.5算法［12］比較分析

文獻［13］中的表1訓練集（1～10行），因篇幅原因經相應等價后，只對分辨度較高的6個條件屬性列表，見表2。

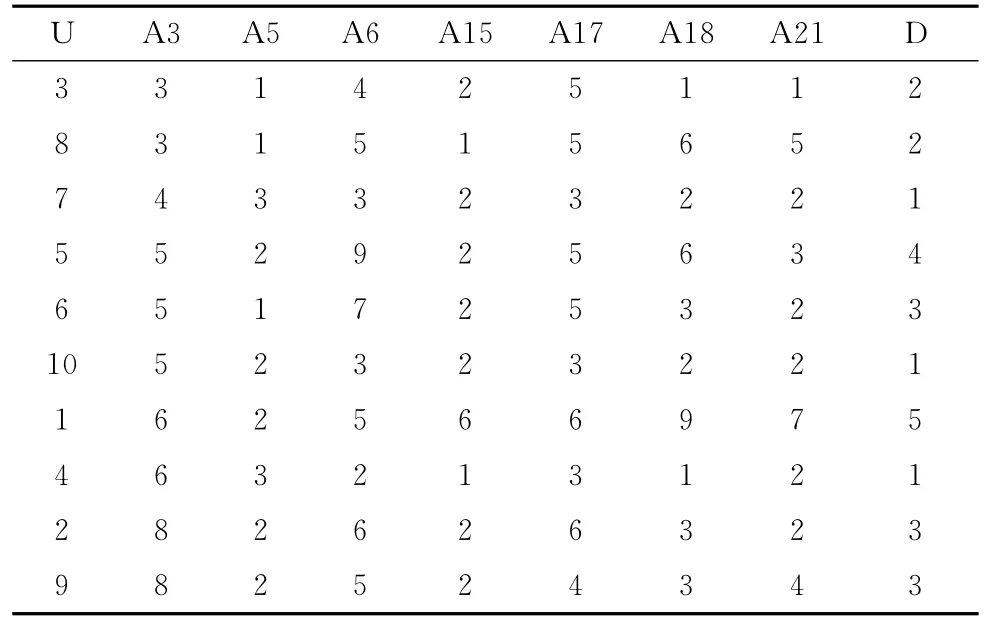
表2 標準化后的決策數據

A3有5個粒（A3，3），（A3，4），（A3，5），（A3，6），（A3，8）。參見2.1的算法，對于（A3，3）有（Lw（A3，3）＝2，Bn（A3，3）＝1）；對于（A3，4）有（1，1）；對于（A3，5）有（3，4）；對于（A3，6）有（2，3）；對于（A3，8）有（2，1）。

LwA3＝∑LwA3v＝∑（WA3（v）／SD（u））＝2＋1＋3＋2＋2＝10；BnA1＝（∑SD（u）｜LWA1）＝1＋1＋4＋3＋1＝10。

則A3平均極大葉枝粒比為ALB（A3）＝10／10＝1。

A5有3個粒（A5，1），（A5，2），（A5，3）。對于（A5，1）有（Lw（A5，1）＝3，Bn（A5，1）＝3）；對于（A5，2）有（5，5）；對于（A5，3）有（2，1）。

LwA5＝∑LwA5v＝∑（WA5（v）／SD（u））＝3＋5＋3＝10；BnA5＝（∑SD（u）｜LWA5）＝3＋5＋1＝9。

則A5平均極大葉枝粒比為 ALB（A5）＝10／9＝1.1

同理，

所以 Max（ALB（Ai））（3，5，6，15，17，18，21）＝ALB（A5）∪ALB（A15）∪ALB（A18）∪ALB（A21）

由于A5、A15、A18、A21分辨力相同，都可得9枝7葉決策樹，則要根據首層N（Ai）中被分辨出的情況進行再次分辨。A5首層完全分辨出1個粒（A5，3），其WA5（3）＝2；A15首層分辨出1個粒（A15，6），其 WA15（6）＝1；A18首分出3個粒（A18，2）、（A18，3）、（A18，9），其∑WA18（v）＝2＋3＋1＝6；A21首分出5個粒，其∑WA21（v）＝5。由于首層分辨出的 WAi（v）越大則樹越優，所以得首選順序為A18、A21、A5、A15。

首選屬性A18、A21、A5、A15之一都可得9枝7葉樹，而首選屬性A18則得最優樹（首層葉最重）。將首選A18和A17（文獻［14］算法）比較如下（→示樹枝，D.k示樹葉）：

首選A18和A17屬性都為2層樹，A18首層完全分辨出3個粒，總重量為6；而A17分辨出2個粒，總重量為4。A18為9枝7葉樹；而首選A17只可得10枝8葉樹。顯然，雖然C4.5克服了ID3用信息增益選擇屬性時偏向取值多的屬性，但確定劃分屬性的準確性仍不足。

2.3 與相對核的算法比較分析

文獻［14］中表1經等價標準化后見表3，表中的屬性A3中共包括3個粒：（A3，0），（A3，1），（A3，2）。在表3各基本粒的劃分集中求Lw（A1，v）和Bn（Ai，v），其中v＝0，1，2。

A3有5個粒（A3，0），（A3，1），（A3，2）。

對（A3，0）行集，最優列為 A3，WA1（0）／SD（0）＝1／1＝1，SD（0）＝1，記為（1，1）。

對（A3，1）行集，最優列為 A4，∑（WA4（0，1，2）／SD（u））＝（2／1＋3／1＋5／2）＝7.5，記為（7.5，5）。

對（A3，2）行集，最優列為 A5，∑（WA5（0，1，2）／SD（u））＝（1／1＋1／1＋3／2）＝3.5，記為（3.5，5）。

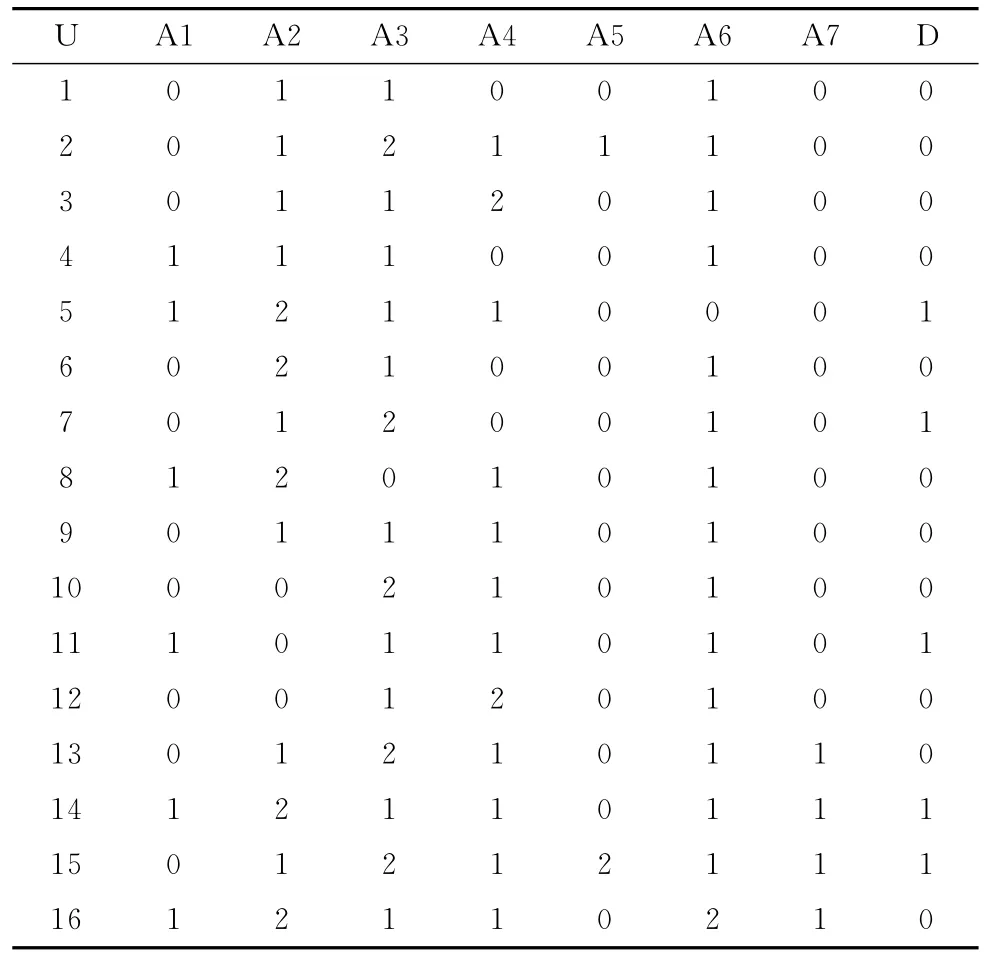
表3 標準化后的決策數據

所以，

LwA3＝∑LwA3v＝∑（WA3（v）／SD（u））＝1＋7.5＋3.5＝12，BnA3＝（∑SD（u）｜LWA3）＝1＋5＋5＝11，則A3平均極大葉枝粒比為 ALB（A3）＝12／11＝1.09。

對（A4，0）行集，最 優列為 A3，∑ WA3（1，2）／SD（u）＝（3／1＋1／1）＝4，記為（4，3）。

對（A4，1）行集，最優列為 A5，∑（WA5（0，1，2）／SD（u））＝（1／1＋1／1＋8／2）＝6，記為（6，5）。

對（A4，2）行集，最優列為 A4，WA4（2）／SD（u））＝2／1＝2，記為（2，1）。

所以，

LwA4＝∑LwA4v＝∑（WA4（v）／SD（u））＝4＋6＋2＝12，BnA4＝（∑SD（u）｜LWA4）＝3＋5＋1＝9。

則A4平均極大葉枝粒比為 ALB（A4）＝12／9＝1.33。

類似地，LwA5＝2＋2＋4＋1＋1＝10，BnA5＝6＋1＋1＝8，ALB（A5）＝10／8＝1.25。

LwA6＝2＋4＋2＋1＋1＝10＝10，BnA6＝1＋1＋6＝8，ALB（A5）＝10／8＝1.25。

經ALB（Ai）（i＝3，4，5，6）比較可得單屬性分辨強度順序：A4、A5、A6、A3，證明以核屬性作為首選劃分屬性并非可得最優樹［14］。

3 結束語

本文以粒計算［7］為理論依據，提出以屬性的葉枝粒比確定劃分屬性的算法：將屬性劃分為若干基本粒，以粒的葉枝比預測其劃分后可能的最好情況代表該粒最強分辨能力，以屬性中各基本粒的最強分辨能力之累加和作為該屬性的最強分辨能力，而表中屬性分辨能力最強者為劃分屬性。按劃分屬性建立結點，依此逐級遞規劃分得最優決策樹。算法不涉及概率計算和指數對數復雜運算（信息增益算法）和屬性約簡復雜過程（粗糙集算法），具有準確度高、算法簡潔的特點。

［1］DING Chunrong，LI Longshu，YANG Baohua.Decision tree constructing algorithm based on rough set ［J］.Computer Engineering，2010，36 （11）：75－77 （in Chinese）. ［丁春榮，李龍澍，楊寶華.基于粗糙集的決策樹構造算法 ［J］.計算機工程，2010，36 （11）：75－77.］

［2］ZHANG Fenglian，LIN Jianliang.New method of building decision tree ［J］.Computer Engineering and Applications，2009，45 （10）：141－143 （in Chinese）.［張鳳蓮，林健良.新的決策樹構造方法 ［J］.計算機工程與應用，2009，45（10）：141－143.］

［3］XU Fen，JIANG Yun，WANG Yong，et al.Improved algorithm for attribute reduction based on rough sets and information gain ［J］.Computer Engineering and Design，2009，30（24）：5698－5700 （in Chinese）. ［徐分，蔣蕓，王勇，等.基于粗糙集和信息增益的屬性約簡改進方法 ［J］.計算機工程與設計，2009，30 （24）：5698－5700.］

［4］GAO Jing，XU Zhangyan，SONG Wei，et al.New decision tree algorithm based on rough set model ［J］.Computer Engineering，2008，34 （3）：9－11 （in Chinese）. ［高靜，徐章艷，宋威，等.一種新的基于粗糙集模型的決策樹算法 ［J］.計算機工程，2008，34 （3）：9－11.］

［5］GONG Gu，HUANG Yongqing，HAO Guosheng.Analysis and improved implementation of decision tree algorithms ［J］.Computer Engineering and Applications，2010，46 （13）：139－141（in Chinese）.［鞏固，黃永青，郝國生.決策樹算法的優化研究 ［J］.計算機工程與應用，2010，46 （13）：139－141.］

［6］CHEN Xi，LEI Jian，FU Ming.Attribute reduction algorithm for rough set based on improving genetic algorithm ［J］.Computer Engineering and Design，2010，31 （3）：602－607 （in Chinese）.［陳曦，雷健，傅明.基于改進遺傳算法的粗糙集屬性約簡算法 ［J］.計算機工程與設計，2010，31 （3）：602－607.］

［7］XU Jiucheng，SHI Jinling，CHENG Wanli.Algorithm for decision rules extraction based on granular computing ［J］.Com－puter Engineering and Applications，2009，45 （25）：132－134（in Chinese）.［徐久成，史進玲，成萬里.粒計算中決策規則的提取 ［J］.計算機工程與應用，2009，45 （25）：132－134.］

［8］LI Hong，MA Xiaoping.Research on feature and formal representation of granule ［J］.Computer Engineering and Applications，2011，47 （11）：3－6 （in Chinese）.［李鴻，馬小平.粒的特征及形式化表示研究 ［J］.計算機工程與應用，2011，47（11）：3－6.］

［9］WANG Yongmei，HU Xuegang.Research of ID3algorithm in decision tree ［J］.Journal of Anhui University（Natural Science Edition），2011，35 （3）：71－75 （in Chinese）.［王永梅，胡學鋼.決策樹中ID3算法的研究 ［J］.安徽大學學報 （自然科學版），2011，35 （3）：71－75.］

［10］YANG Jing，ZHANG Nannan，LI Jian，et al.Research and application of decision tree algorithm ［J］.Computer Technology and Development，2010，20 （2）：114－120 （in Chinese）.［楊靜，張楠男，李建，等.決策樹算法的研究與應用 ［J］.計算機技術與發展，2010，20 （2）：114－120.］

［11］ZHANG Lin，CHEN Yan，LI Taoying，et al.Research on decision tree classification algorithms ［J］.Computer Engineering，2011，37 （13）：66－70 （in Chinese）. ［張琳，陳燕，李桃迎，等.決策樹分類算法研究 ［J］.計算機工程，2011，37 （13）：66－70.］

［12］XU Peng，LIN Sen.Internet traffic classification using C4.5 decision tree ［J］.Journal of Software，2009，20 （10）：2692－2704 （in Chinese）.［徐鵬，林森.基于 C4.5決策樹的流 量 分 類 方 法 ［J］. 軟 件 學 報，2009，20 （10）：2692－2704.］

［13］ZHANG Li，YAO Yizhan，PENG Jianfen，et al.Intelligent information security risk assessment based on a decision tree algorithm ［J］.Journal of Tsinghua University （Science and Technology），2011，51 （10）：1236－1239. ［張利，姚軼嶄，彭建芬，等.基于決策樹的智能信息安全風險評估方法 ［J］.清華大學學報 （自然科學版），2011，51 （10）：1236－1239.］

［14］CHEN Shilian，LUO Qiujin.Decision tree construction method based on rough set and distance function ［J］.Computer Engineering and Design，2008，29 （12）：3191－3193 （in Chinese）.［陳世聯，羅秋瑾.基于粗集和距離函數的決策樹構造方 法 ［J］. 計 算 機 工 程 與 設 計，2008，29 （12）：3191－3193.］