DE優化T－S模糊神經網絡的交通流量預測

侯 越

（蘭州交通大學 電子與信息工程學院，甘肅 蘭州730070）

0 引 言

智能交通系統 ITS （intelligent transportation system）是全方位解決交通擁擠與交通運輸安全的有效手段。交通控制和交通誘導是ITS的重要組成部分，實時準確的交通流量預測是實現智能交通控制和交通誘導的前提和關鍵［1］。城市交通流具有明顯的混沌特征，其短時交通流數據具有高度非線性、隨機性和不確定性等特點，是一種典型的混沌時間序列問題。迄今為止，很多專家學者在這一領域做了很多研究，建立了多種交通流預測模型，如支持向量機［2］、Kalman濾波器 模 型［3］、Volterra濾 波 器 模 型［4］、非參數回歸［5］、貝葉斯組合模型［6］、RBF神經網絡模型［7］和T－S模糊神經網絡模型［8］，在這些預測方法中，神經網絡方法因具有良好的學習能力與泛化推廣能力，成為了大量學者研究的熱點。但在實際應用中，神經網絡中連接權值和閾值的取值對它的性能有著較大的影響［9］。差分進化（differential evolution，DE）算法是由Storn和Price提出的一種基于群體優化算法［10］，它不僅具有很強的全局尋優能力，而且具有易用性、穩健性和容易實現，非常適用于神經網絡參數優化。

本文從非線性時間序列角度出發，提出了一種DE優化T－S模糊神經網絡的方法 （DETSFNN），該方法利用DE來彌補T－S模糊神經網絡連接權值和閾值選擇上的隨機性缺陷，從而能發揮T－S模糊神經網絡泛化的映射能力，而且能使T－S模糊神經網絡具有較快的收斂性以及較強的學習能力。利用該方法對實測交通流量進行建模和預測分析，結果表明該方法對于交通流量預測具有更好的非線性擬合能力和更高的預測準確性。

1 基本DE算法

DE算法是一種基于群體進化的隨機搜索算法，具有記憶個體最優解和群內信息共享的特點［8］。算法首先取得一組隨機初始化的種群：，NP 是種群規模，種群維數為D。經過一系列的操作，第t代個體進化為。算法的基本思想是：父代兩個不同隨機個體相減得到的差分矢量加權后，根據一定規則加到隨機選擇的第三個個體上，按照一定的概率，父代個體與變異個體進行交叉操作，生成一個新個體，然后在父代個體與這個新個體根據適應度函數值的大小進行選擇操作，選擇適應度更優的個體作為子代。

1.1 變異操作 （mutation operation）

變異操作可防止進化陷入局部最優解。DE最基本的變異成分是父代的差分矢量，每個矢量對包括父代群體中兩個不同的個體，根據變異個體的生成方式不同，可形成多種不同的進化方案，最基本的變異如式 （1）所示

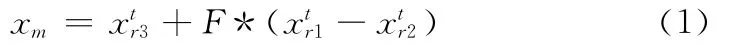
1.2 交叉操作 （crossover operation）

DE利用交叉操作來保持群體的多樣性。交叉策略為：群體目標矢量個體xti與變異個體xm進行交叉操作，產生試驗個體xT。為確保個體的進化，使xT至少有一位由xm貢獻，其他位則利用交叉概率因子CR，交叉操作的方程如式（2）所示

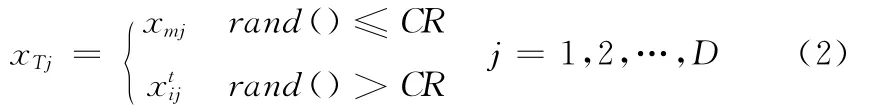
式中：rand（）—— ［0，1］之間的隨機數，CR ∈ ［0，1］，CR越大，越有利于加速收斂速度，CR越小，越有利于保持群體的多樣性和全局搜索。

1.3 選擇操作 （selection operation）

DE采用貪婪的搜索策略，選擇適應度函數值高的作為子代，選擇操作方程如式 （3）所示

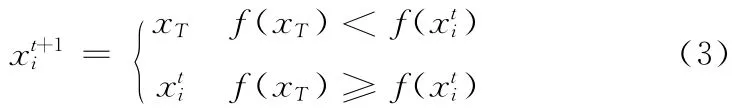
2 T－S模糊神經網絡結構

對于一個MISO（多輸入單輸出）系統，設輸入變量X＝［x1，x2，…，xn］T，每個分量xi均為模糊語言變量，并設A（xi）＝ ｛A1i，A2i，…，Ami｝，i＝1，2，…，n，其中Aji（j＝1，2，…，m）是xi的第j個語言變量值，它是定義在論域xi上的一個模糊集合，相應的隸屬函數為μAji（xi），其中i＝1，2，…，n；j＝1，2，…，m ，則T－S模糊規則可用式 （4）表示

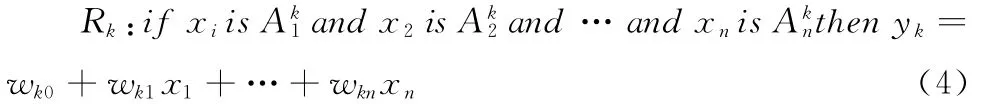
式中：Rk——第k條規則，k＝1，2，…，z；z≤mn。

模糊系統的輸出量為每條規則輸出量的加權值，輸出如式 （5）所示

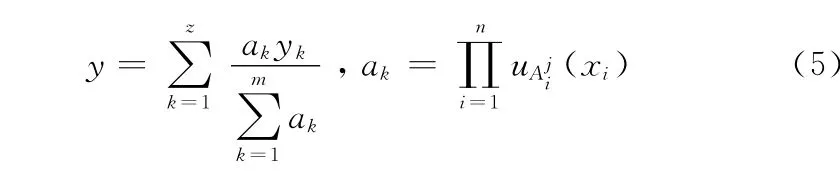
根據上面給出的模糊，可設計出如圖1所示的模糊神經網絡。該網絡由前件網絡和后件網絡兩部分組成，前件網絡用來匹配模糊規則，后件網絡用來產生模糊規則，具體各層描述參見文獻 ［8］。

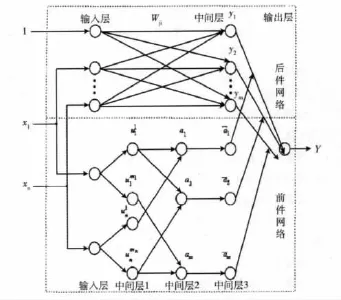
圖1 T－S模糊神經網絡結構

3 差分優化T－S模糊神經網絡的算法設計

3.1 基本思想

DETSFNN的基本思想是：列出神經網絡中可能存在的神經元，將這些神經元在開始訓練前所有可能存在的連接權值和閾值編碼成二進制碼串或者實數碼串表示的個體，進而隨機地生成這些碼串的群體，并加上隨機選擇、變異和交叉用來提高種群的多樣性，經過上述變異、交叉操作，產生一個新的臨時種群，利用保優策略的選擇操作對種群的個體進行優化選擇，從而又產生新一代種群，種群按照以上過程不斷優化直至找到最優個體。將DE得到的最優個體對T－S模糊神經網絡的初始權值和閾值進行賦值，再利用T－S模糊神經網絡預測模型進行尋優，從而得到具備全局最優解的T－S模糊神經網絡預測值。

3.2 DE優化T－S模糊神經網絡算法

算法的基本步驟如下：

步驟1 編碼。DE算法使用的是實數編碼方式，估個體編碼的長度與其變量的個數相等。本文對T－S模糊神經網絡的參數wij，cj，θj，ε進行統一編碼到一個個體中，每一個個體就能代表一個T－S模糊網絡結構。

步驟2 初始化種群以及算法的參數。設種群規模為NP，隨機生成NP個個體的初始種群W ＝ （W1，W2，…，Wp）T，給出收縮因子F和交叉概率因子CR的初始值，令迭代計數器初值t＝0，設定算法的最大迭代數k，得到個體Wi的一個實數向量w1，w2，…，wt作為DE的一個染色體。

步驟3 按照式 （6）計算第g代每個個體的適應度函數值，找出該代最優個體。

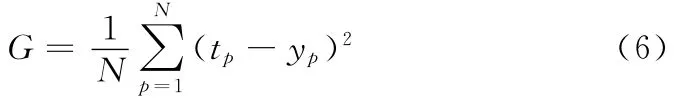
式中：N——訓練樣本的總數；tp——第P個樣本的期望輸出；yP——第P個樣本的實際輸出。

步驟4 對最優個體執行步驟5—步驟7操作，生成第g＋1代種群。

步驟5 變異。根據式 （1）對個體Wi進行變異，生成變異個體W′i。

步驟6 交叉。將生成的變異個體Wi與W′i按照式（2）進行交叉操作，生成新個體WT。

步驟7 選擇。將Wi與WT代入目標函數值中，根據式 （3）選出適應度函數值小的個體W′T作為新種群的個體。

步驟8 g＝g＋1；

步驟9 若迭代計數器的值超過了最大進化次數k，或者達到用戶設置的精度要求，則退出操作，否則返回步驟4執行。

步驟10 將DE優化得到的個體分解成為T－S模糊神經網絡的連接權值和閾值，以此作為預測模型的初始權值和閾值，訓練T－S模糊神經網絡預測網絡，得出交通流量預測的最優解。

4 仿真實驗

將本文提出的DETSFNN預測模型應用于實測交通流時間序列的預測，并與T－S模糊神經網絡 （TSFNN）預測模型進行對比，以此驗證該算法的有效性。

4.1 預測評價標準

實驗的誤差評價主要用到相對均方誤差RE，均方根誤差RMSE和正則化均方根誤差NRMSE，即

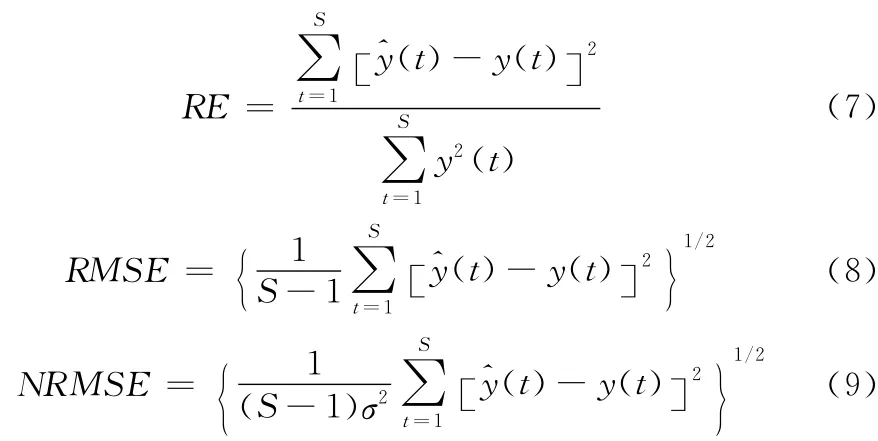
式中：S——預測樣本數，y′（t）、y（t）——預測值、期望值，σ——目標時間序列的標準方差。運用式 （10）對實驗中的時間序列數據進行歸一化，并對歸一化后的時間序列按照式 （11）進行相空間重構

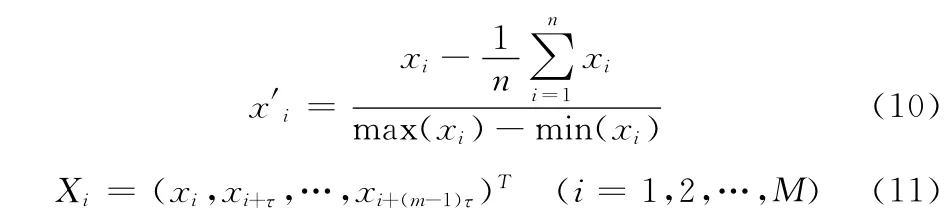
式中：｛xi｝——原時間序列，｛ x′i｝——歸一化后的時間序列。M＝n－（m－1）τ——重構空間中的個數；τ——延遲時間；m——嵌入維數。

4.2 實測交通流時間序列預測

在單位時間內，通過道路某一觀測點或者斷面的車輛數，稱為交通流量亦稱為交通流或交通量，其統計方法如式 （12）所示

式中：V——某一時刻t的交通流量，T——統計時間間隔，N——T時段內的車流數量。

該實驗交通流數據來自北京某公路監測站的實測數據，觀測總時間為4天共96小時。以15分鐘為時間間隔，記錄每個時段的車輛數，并按式 （12）分別計算出各個時間點的交通流量值，總共384組數據。采用文獻 ［11］中計算最大Lyapunov指數的改進算法，計算得該交通流時間序列的最優嵌入維數m為4，最優延遲時間τ為1，最大Lyapunov指數為0.0392，說明該交通流時間序列亦為混沌時間序列。

取交通流序列前288組為訓練樣本，后92組數據為測試樣本。分別用TSFNN模型、DETSFNN模型對其進行預測，圖2給出了在m＝4，τ＝1的TSFNN模型預測結果，圖3給出了在m＝4，τ＝1的TSFNN模型預測結果。表1給出了兩種預測模型在不同延遲時間、嵌入維數下的NRMSE預測誤差。

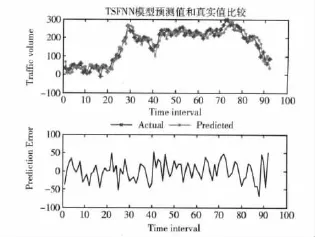
圖2 TSFNN模型預測結果

表1 基于不同延遲時間和嵌入維數的預測誤差

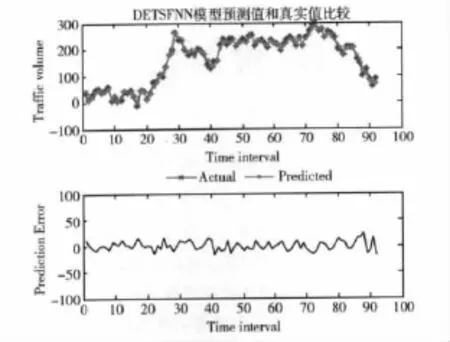
圖3 DETSFNN模型預測結果

從圖2、圖3和表1可以看出兩種預測模型的預測結果均能就很好地預測交通流量變化的趨勢，DETSFNN模型的預測精度高于TSFNN模型，從而說明DETSFNN模型對于實測交通流時間序列的預測是有效地。從表1還可以看出當m和τ取最優延遲時間和嵌入維數時，預測效果最佳。

5 結束語

針對交通誘導與控制對實時性的高要求，以及交通流所顯示的非線性、不確定性，本文從非線性時間序列角度出發，提出了一種DE優化T－S模糊神經網絡的交通流量預測方法，將其應用于實測交通流系統的預測，并與T－S模糊神經網絡預測模型進行了預測精度的比較。結果表明，該模型在交通流量預測方面具有更好的非線性擬合能力和更高的預測精度。

［1］SHEN Guojiang，WANG Xiaohu，KONG Xiejie.Short－term traffic volume intelligent hybrid forecasting model and its application ［J］.Systems Engineering Theory ＆ Pratice，2011，31（3）：561－568 （in Chinese）.［沈國江，王嘯虎，孔祥杰.短時交通流量智能組合預測模型及應用 ［J］.系統工程理論與實踐，2011，31 （3）：561－568.］

［2］Castro Neto M，Jeong Y S，Jeong M K，et al.Online SVR for short－term traffic flow prediction under typical and atypical traffic conditions ［J］.Expert Systems with Applications，2009，36 （3）：6164－6173.

［3］NIE Peilin，YU Zhi，HE Zhaocheng.Constrained Kalman filter combined predictor for short－term traffic flow ［J］.Journal of Traffic and Transportation Engineering，2008，8 （5）：86－90.（in Chinese）.［聶佩林，余志，何兆成.基于約束卡爾曼濾波的短時交通流量組合預測模型 ［J］.交通運輸工程學報，2008，8 （5）：86－90.］

［4］LI Song，LIU Lijun，GUO Hailing.Comparative of the predictive method of chaos in short－term traffic flow ［J］.Systems Engineering，2009，27 （9）：60－64 （in Chinese）. ［李松，劉力軍，郭海玲.短時交通流混沌預測方法的比較 ［J］.系統工程，2009，27 （9）：60－64.］

［5］Smith B L，Williams B M，Oswald R K.Comparison of parametric and nonparametric models for traffic flow forecasting［J］.Transportation Research Part C：Emerging Technologies，2002，10 （4）：303－321.

［6］ZHENG Weizhong，SHI Qixin.Study of short－term freeway traffic flow prediction based on Bayesian combined model ［J］.China Journal of Highway and Transport，2005，18 （1）：85－89 （in Chinese）.［鄭為中，史其信.基于貝葉斯組合模型的短期交通量預測研究 ［J］.中國公路學報，2005，18 （1）：85－89.］

［7］ZHANG Yumei，QU Shiru，WEN Kaige.A short－term traffic flow forecasting method based on chaos and RBF neural network［J］.Systems Engineering，2007，25 （11）：30－34 （in Chinese）.［張玉梅，曲仕茹，溫凱歌.基于混沌和RBF神經網絡的短時交通流量預測 ［J］.系統工程，2007，25 （11）：30－34.］

［8］ZHANG Ying.T－S fuzzy neural network based on deviation compensation ［J］.Journal of Jiangnan University，2010，9（4）：481－484 （in Chinese）.［張穎.基于偏差補償的T－S模糊神經網絡 ［J］.江南大學學報，2010，9 （4）：481－484.］

［9］ZHU Wanfu，ZHAO Shijun.Optimal design of structure for neural networks based on rough sets ［J］.Computer Engineering and Design，2007，28 （17）：4210－4212 （in Chinese）.［朱萬富，趙仕俊.基于粗糙集的神經網絡結構優化設計 ［J］.計算機工程與設計，2007，28 （17）：4210－4212.］

［10］Storn R，Price K.Minimizing the real functions of the ICEC＇96contest by differential evolution ［C］／／Proc of IEEE Int Conf on Evolutionary Computation，1996：842－844.

［11］LI Song，HE Guoguang.Identification of chaos in the traffic flow based on the improved largest Lyapunov exponents algorithm ［J］.Journal of Wuhan University of Technology，2006，30 （5）：747－750 （in Chinese）. ［李松，賀國光.基于最大Lyapunov指數改進算法的交通流混沌判別 ［J］.武漢理工大學學報，2006，30 （5）：747－750.］