有源電力濾波器的Matlab仿真
高 勇
(四川省電力公司信息通信公司,四川 成都 610041)
0 引言
自20世紀70年代以來,由于電力電子技術及半導體技術的飛速發展,使得各種電力電子裝置在電力系統、工業、交通及家庭中得到了越來越廣泛的應用,然而,由諧波所造成的危害也越來越嚴重了。由于諧波的存在,不僅會使得電能在生產、傳輸和利用過程中的效率降低,而且還會導致電氣設備的使用壽命因過熱、產生振動和噪聲、絕緣老化而縮短,甚至還可能引起電氣設備故障或燒毀[1]。同時,諧波的存在也常常會引起繼電保護和自動裝置的誤動作從而引起電能計量出現混亂[2]。在電力系統外部,諧波對通信設備和電子設備也會產生嚴重的干擾。因此,諧波問題受到了世界各國的普遍關注,諧波的治理成為了一大研究熱點。目前,對于諧波的治理主要有采用無源濾波裝置和有源濾波器(active power filter,APF)。有源電力濾波器的濾波效果非常好,在其額定的無功功率范圍內,可以實現完全濾波。然而,有源電力濾波器是一個復雜非線性的控制系統,要對其進行精確地理論分析是比較困難的,所以通過用模擬仿真實驗的方式來驗證控制系統就顯得非常必要[3,4-7]。
在Matlab中有許多實用的工具箱,如控制系統工具箱、濾波器設計工具箱、通信工具箱等。Simulink是基于Matlab的框圖設計環境,可以用來對各種動態系統進行建模、分析和仿真,而且Simulink還提供了豐富的功能塊以及不同的專業模塊集合[6]。因此,這里擬采用利用Matlab對有源電力濾波器進行動態的系統仿真。
1 Matlab仿真簡介
Matlab及其Simulink環境下的仿真平臺在控制系統仿真中應用很普遍,仿真環境界面簡單。
Simulink是一個能對動態系統進行建模、仿真和分析的軟件包。它支持線性和非線性系統連續和離散時間模型,或者是兩者混合的模型,可方便迅速地建立起各種非線性或線性的模型。Simulink模型不僅能讓用戶知道具體的環節動態細節,隨時觀察仿真過程中系統各處的動態變化,而且能清晰地了解各器件、各系統間的信息交換,掌握各部分之間的交互影響[3,5-7]。
2 諧波計算仿真模型
要對諧波進行計算,則設計了諧波計算仿真模型、三相/兩相的轉換模型和兩相/三相的轉換模型。
諧波檢測模型采用ip-iq方式算法。如圖1所示,非線性負載電流 ia、ib、ic經過3/2變換、C運算后得到有功電流ip和無功電流iq;經低通濾波器濾波得到其直流分量,然后進行C反變換、2/3變換得到基波電流,然后負載電流與基波電流相減后便得到諧波電流分量。

圖1 諧波計算模型
在該運算方式中,需要與A相電網電壓同相位的正弦信號sinωt和余弦信號cosωt,在仿真模型的建立中,用鎖相環和正余弦信號發生電路模型產生,如圖2所示。
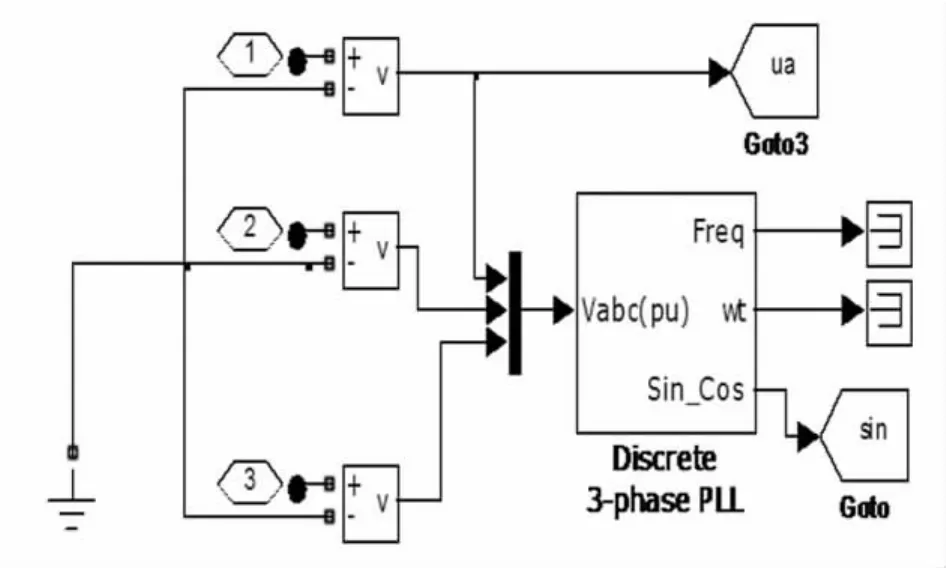
圖2 PLL與正余弦信號發生模型
圖3為三相負載電流經過C32C變換后得到兩相有功電流和無功電流的過程,其中模型中的sincos為與A相電壓同相位的正、余弦信號。
在ip-iq方式算法來進行諧波電流檢測時,有一個低通濾波環節,用于從有功和無功電流中檢出其直流分量。低通濾波算法的性能直接決定著諧波檢測的精確性和動態跟蹤速度,影響著有源電力濾波器諧波補償的性能。設計的基本原則是:應保證對直流分量的增益為1,并盡可能衰減交流分量。目前常用的濾波器形式有FIR濾波器(非遞歸模型)和IIR濾波器(遞歸模型)。FIR濾波器的優點是可以精確到線性相位,但維數一般很高,而IIR濾波器在維數不需要很高的情況下就能滿足一定的指標。這里選用的是2階ButterWorth濾波器,在低頻段,該濾波器具有較好的檢測精確性。

圖3 三相/兩相轉換模型
兩相/三相變換的仿真模型如圖4所示,有功和無功電流的直流分量經過C-1C23變換后,輸出三相負載電流的基波分量 iaf、ibf、icf。

圖4 兩相/三相轉換模型
3 PWM信號控制主電路仿真模型
有源電力濾波器的主電路由逆變器組成,主要用于在特定PWM脈沖的控制下補償交流電網存在的諧波電流[8]。PWM信號產生及控制變流器的仿真模型如圖5所示,該模型的輸入電流為ipwm,它是諧波電流與逆變器輸出電流的差值,通過滯環比較來控制逆變器開關器件的通斷,從而產生補償諧波電流。

圖5 PWM信號控制模型
4 系統仿真模型及參數設置
(1)系統仿真模型

圖6 APF系統模型
該仿真模型主要包括了諧波源產生電路、諧波計算模塊、PWM信號產生并控制變流器產生補償電流的模塊。
(2)參數設置
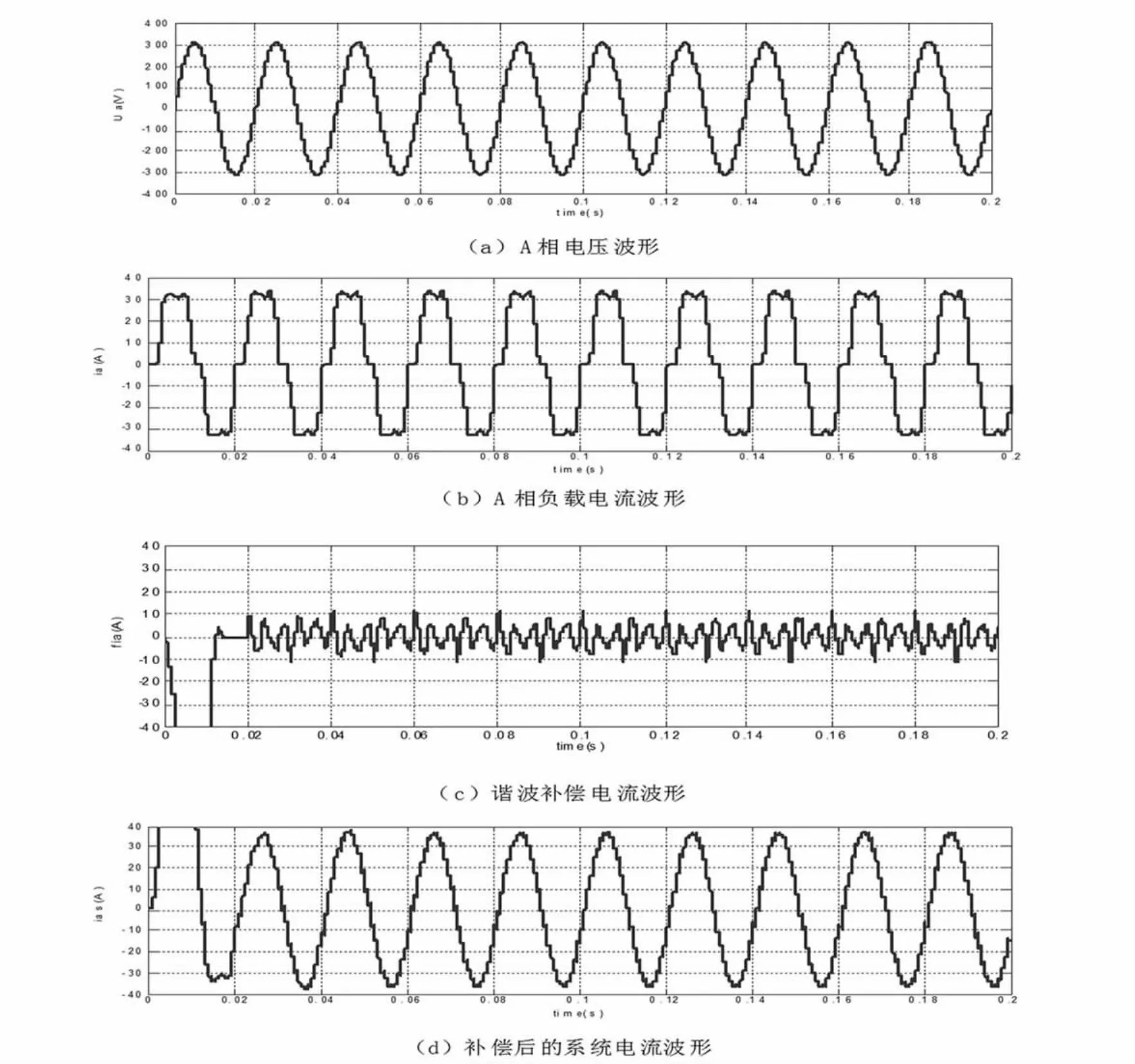
圖7 APF系統的仿真波形
采用相電壓為220 V,頻率為50 Hz的三相對稱系統。為了使有源電力濾波器在工作時有一個較好的補償效果和較快的反應速度,變流器直流側的電壓要超過其線電壓的2倍以上[9],這里控制直流側的電壓選擇為750 V。
選定的電容值為2000 μF,輸出電感值為2 mH。
5 仿真結果與分析
仿真結果如圖7(a)、(b)、(c)、(d)所示。
由仿真波形可以看出,原來由于非線性負荷所造成的電流波形發生嚴重的畸變,在接入APF進行諧波電流補償以后,該系統電流的波形基本上為一個正弦波形,從而達到了濾波效果。通過進行FFT頻譜分析之后,得到諧波含量和總諧波畸變率:總諧波畸變率在補償前達到了近18.5%,補償之后不到2.1%;各次諧波的補償率均達到了90%以上。由此可見該仿真濾波器系統基本上實現了諧波補償的功能。
6 結論
根據有源濾波器系統結構的組成,搭建了基于Matlab-Simulink仿真環境下的系統模型,并對各個模塊分別給予仿真結果以及結論分析。通過仿真結果可以發現,各仿真模塊能夠完成模塊的功能,整個系統能夠完成濾波任務。
[1]張永剛,陳海嘯.諧波危害及治理探討[J].技術與市場,2012,19(3):73.
[2]曹璐,王富生.淺談諧波對電能表計量的影響[J].科技向導,2012(3):338.
[3]年珩,全宇.諧波電網電壓下PWM整流器增強運行控制技術[J].中國電機工程學報,2012,32(9):41-49.
[4]蘇奎峰,呂強,耿慶鋒,等.TMS320F2812原理與開發[M].北京:電子工業出版社,2005.
[5]王亮,趙玲.電力有源濾波器的Matlab仿真[J].上海電力學院學報,2005,21(1):21-26.
[6]王忠禮,段慧達,高玉峰.MATLAB應用技術:在電氣工程與動化專業中的應用[M].北京:清華大學出版社,2007.
[7]劉海峰,陳梅.基于MATLAB的電力有源濾波器(APF)的仿真[J].電氣開關,2006,44(4):35-37.
[8]吳春芳,程漢湘,朱約章,等.并聯型有源電力濾波器的MATALB 仿真研究[J].節能技術,2005,23(2):118-121.
[9]陳慶國,趙春明.三相四線制并聯型電力有源濾波器的算法和參數仿真[J].電機與控制學報,2009,13(1):20-24.

