基于回歸設計技術的平面磨削表面粗糙度研究

池龍珠

(江蘇技術師范學院，江蘇常州213001)

磨削技術是機械制造業中實現精密加工最有效、應用最廣的制造技術。表面粗糙度作為磨削表面質量的重要參數之一，直接影響零件的使用性能。由于磨削過程極其復雜，影響加工表面粗糙度的因素眾多，而且各因素之間的各種物理、化學現象伴隨于整個磨削過程，所以對磨削技術的理論研究和實踐應用都存在很大難度，大大限制了磨削加工的科學管理及生產效益的提高。縱觀已有的有關表面粗糙度的研究，諸如形成機制及預測方法等，多為金屬刀具的切削［1－2］，而沒有多少關于砂輪磨削表面粗糙度的研究［3－4］。作者利用試驗設計技術及回歸設計技術，對平面磨削表面粗糙度進行了研究，提出表面粗糙度的預測模型，同時給出利用這個模型控制表面粗糙度、優化磨削條件的方法，以期對表面粗糙度的預測與控制、合理選擇磨削參數提供可資利用的依據。

1 實驗設備、測試方法

實驗選用如下設備與裝備:SGH-600平面磨床(Nakase，Japan)，SJ-210P表面粗糙度測量儀 (Mitutoyo)，WA40(120，200)LmVA225×20×50.8砂輪，工件材料為SKH51高速鋼 (HRC62，100×90×20 mm)。每次實驗前，以單顆粒金剛石對砂輪進行修正，以盡可能減少實驗誤差。表面粗糙度測試方法如圖1所示。每次實驗均測量工件兩端和中間共3點的表面粗糙度，然后取其平均值作為當次實驗的表面粗糙度值。

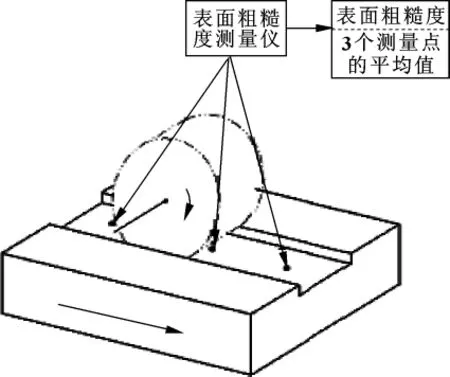
圖1 表面粗糙度測試方法示意圖

2 試驗設計、試驗數據及分析

2.1 試驗設計及試驗數據

眾所周知，影響磨削表面粗糙度的因素有很多。選取砂輪轉速、工件速度、磨削深度、砂輪粒度等4個因素為主要影響因素，每一因素再各取3個水平，如表1所示。然后利用標準正交表L27(313)進行平面磨削實驗。表2為根據所采用的L27(313)正交表配列的每一試驗號的因素、水平以及試驗數據。

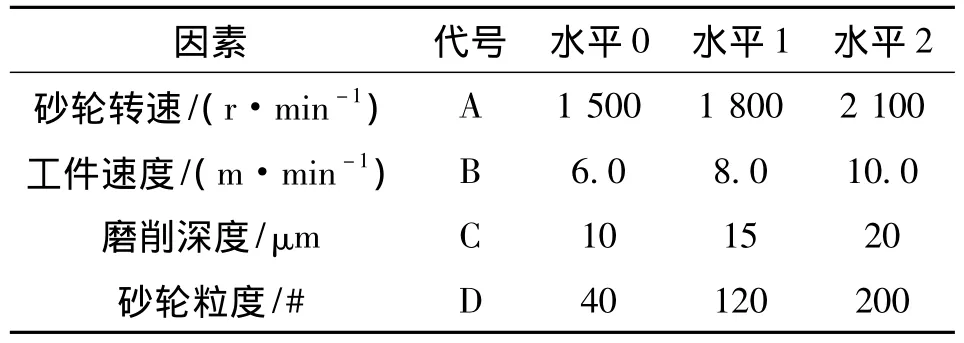
表1 試驗因素、水平選取表因

表2 正交試驗設計及試驗結果

2.2 試驗數據分析

圖2所示為根據試驗號排列的表面粗糙度的試驗結果。

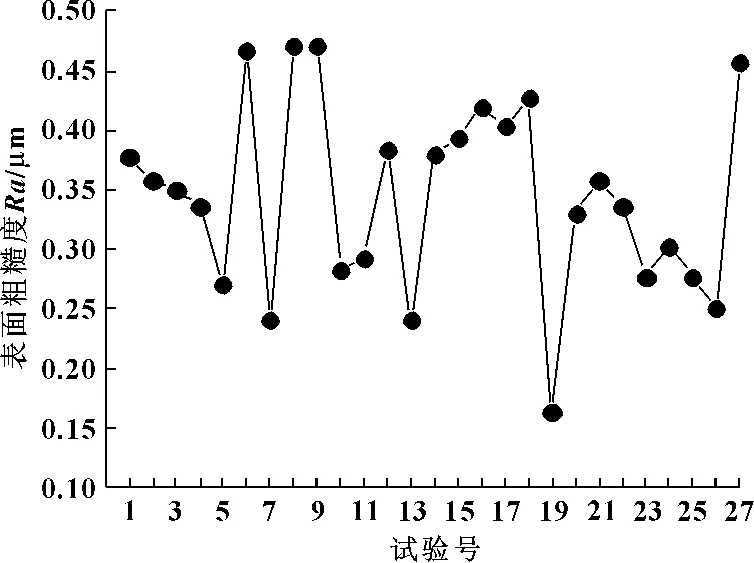
圖2 按著試驗號排列的表面粗糙度試驗值

從圖2可以看出表面粗糙度并沒按著試驗號順序呈現一定的增加或減小的規律性。這正是正交實驗的優點，是由于在每次試驗時，同時改變多個因素的水平所引起的，充分體現正交表的均衡分布思想。

圖3所示為各因素的不同水平下表面粗糙度的分布規律圖，圖中表示了表面粗糙度的最小、最大、中間值、平均值及25%至75%的分布區間。

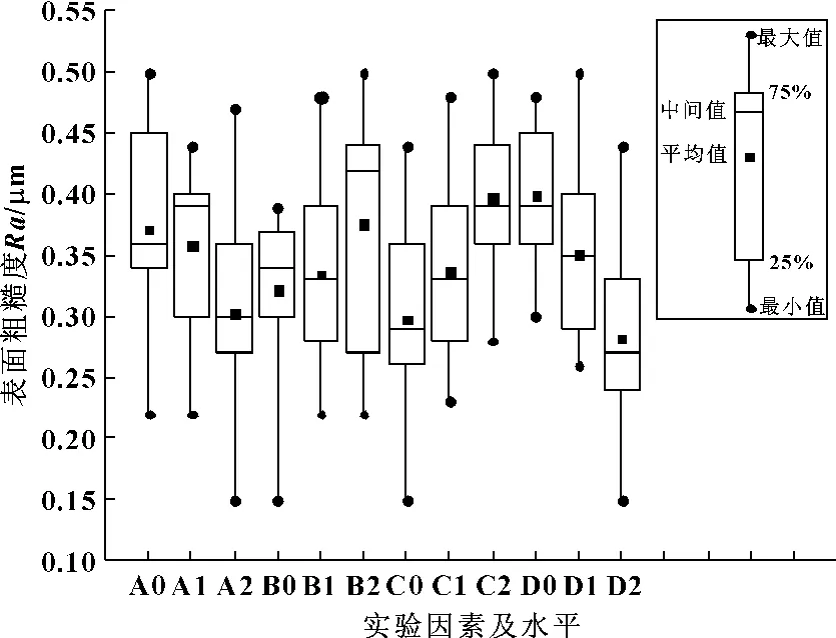
圖3 表面粗糙度分布規律圖

從圖3可以看出砂輪粒度號為200#(D2)和砂輪轉速為2 100 r/min(A2)時，可以獲得較小和較穩定的表面粗糙度。

3 表面粗糙度回歸分析

3.1 表面粗糙度回歸模型的建立

各獨立因素對試驗指標的反應結果，可以用線性回歸設計和非線性回歸設計進行預測。線性回歸設計雖然能簡化計算，但只能回歸出線性方程，而在實際情況下，必須考慮因素的二次或更高次的作用。因此還必須進行非線性回歸設計。通常進行二次回歸設計就可以滿足一般非線性問題的基本要求。由于磨削用量對磨削表面粗糙度的影響不呈現單調線性關系，所以也采用二次回歸設計。通用的二次回歸設計模型［5］如下:

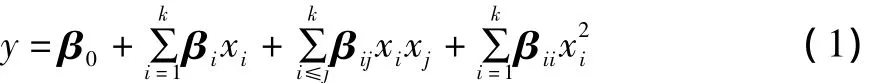
根據公式 (1)，表面粗糙度Ra與各因素之間的二次回歸模型可以用公式 (2)表示。

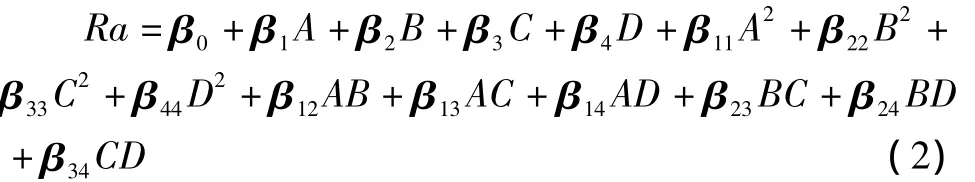
其中系數矩陣β可以用公式 (3)計算。

在式 (3)中，X代表由實驗條件所構成的矩陣(27×15)，Y代表由實驗結果所構成的矩陣 (27×1)。將表2所給出的實驗條件和實驗結果代入式(3)，便能得到系數矩陣β(15×1)，再將所得β代入式 (2)，即可得到下面的二次回歸方程。

3.2 回歸模型的顯著性檢驗

為了驗證回歸模型的顯著性，采用F檢驗法進行檢驗，其結果如表3所示。

表3 回歸模型顯著性檢驗表

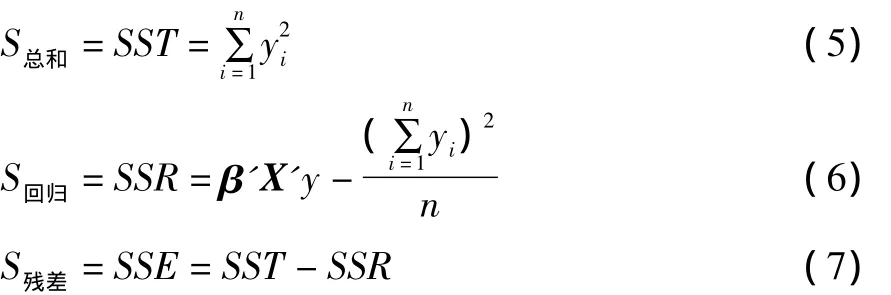
表中各項平方和用公式 (5)計算［6］。為了直觀地了解回歸模型的回歸效果，把實驗值與預測值進行了對比，其結果如圖4所示。

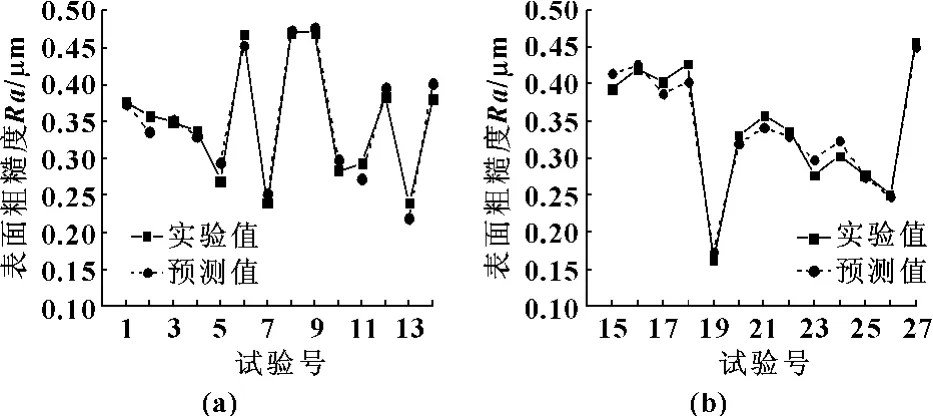
圖4 預測值與實驗值

從表3的檢驗結果及圖4可知回歸方程的回歸效果是良好的。

3.3 回歸模型的決定系數

評價回歸模型精度，除了上述的F檢驗之外，也可以用決定系數來評價，記為r2，即

決定系數r2反映了因變量的變異中能用自變量解釋的比例。其數值在0～1之間。決定系數r2越接近1，說明因變量不確定性的絕大部分能用回歸方程解釋，回歸方程的擬合度好［7］。把表3的相關數據代入公式 (8)即可得出決定系數，即

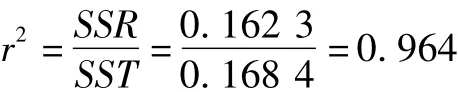
為了更直觀地表達其擬合效果，把實驗值與預測值的對應分散結果用圖5表示。

圖5 實驗值與預測值的對應分散結果

由決定系數r2及圖5可以看出回歸方程的擬合度是良好的。

3.4 實驗驗證

為了進一步驗證回歸效果，選擇沒在表2實驗范圍內的任意4個實驗條件(A1B0C0D2)，(A1B2C1D0)，(A1B1C0D1)，(A2B0C2D1)進行了實驗，同時利用回歸方程進行預測，其比較結果如圖6所示。從圖可以看出回歸模型的預測效果是良好的。

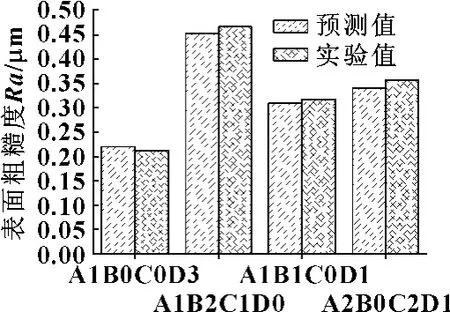
圖6 實驗值與預測值比較

3.5 利用預測模型的表面粗糙度控制與預測

圖7所示為當砂輪轉速為1 500 r/min、砂輪粒度為40#時，根據回歸方程 (4)繪制的反映磨削深度和工件速度對表面粗糙度影響規律的表面粗糙度三維圖。從圖中可以很直觀地看出表面粗糙度隨磨削深度和工件速度變化的規律。

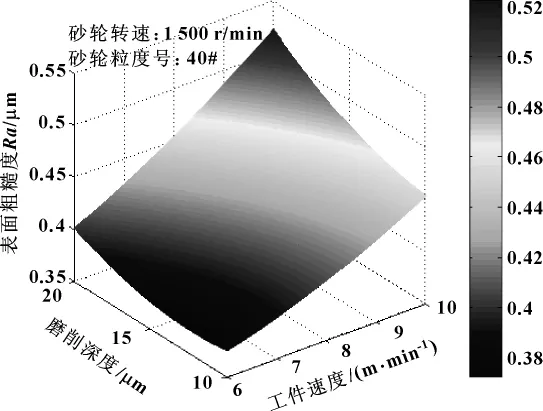
圖7 表面粗糙度三維圖

圖8所示為表面粗糙度二維等值線圖。利用表面粗糙度二維等值線圖可以很方便地對表面粗糙度進行預測和控制。例如當磨削深度為16 μm;工件速度為7 m/min時，表面粗糙度為0.4 μm。若當磨削深度為15 μm時，要想控制表面粗糙度為0.4 μm以下，則工件速度應控制在7.2 m/min以下。

圖8 表面粗糙度二維等值線圖

如圖9所示在表面粗糙度二維等值線圖上附加單位時間金屬切除量MMR曲線，就可以很方便地確定最優參數組合，尋找適宜的工藝條件。單位時間內的金屬切除量MMR可以用下式進行計算。

式中:C代表磨削深度 (μm);B代表工件速度(m/min);b代表砂輪的寬度 (mm，這里取值20 mm)。

由圖9可知，點a與點b的金屬切除量相同，但點b的表面粗糙度低于點a。因此，若選擇點b代表的磨削深度和工件速度，即可在保證金屬切除量相同的前提下獲得更低的表面粗糙度;點a與點c具有相同的表面粗糙度，但點c的金屬切除量大于點a。所以，若選擇點c代表的磨削深度和工件速度，便可在保證表面粗糙度相同的前提下獲得更大的金屬切除量。

圖9 表面粗糙度二維等值線與單位時間金屬切除率

4 結論

采用標準正交表進行4因素3水平的平面磨削試驗，并用回歸設計技術建立了表面粗糙度二次回歸預測模型，并對回歸預測模型進行了F檢驗和決定系數r2檢驗。結果，F0=23.2＞F0.01(14，12)=4.04，r2=0.964，這表明所建立的回歸預測模型達到顯著水平，回歸預測方程具有良好的擬合度。由所建立的二次回歸預測模型，可獲得表面粗糙度二維等值線圖，能直觀地反映表面粗糙度與金屬切除量、磨削用量的關系。這為表面粗糙度的預測與控制，同時選擇合理的磨削參數提供了有價值的參考依據，是一種簡便有效的方法。

【1】石文天，劉玉德，丁悅，等．PCD刀具微細車削硬鋁合金的表面質量研究［J］．機床與液壓，2011，39(17):15－17．

【2】楊濟森，郭宏偉，李洪濤．航空鋁7050高速銑削表面粗糙度試驗研究［J］．機械制造與自動化，2011，40(3):34－35．

【3】李國發，王龍山，丁寧．基于進化神經網絡外圓縱向磨削表面粗糙度的在線預測［J］．中國機械工程，2005，16(3):223－226．

【4】許峰，謝勇，單世遠，等．基于Matlab圖像處理的磨削表面粗糙度的檢驗［J］．工具技術，2011，45(10):83 －84．

【5】任露泉．回歸設計及其優化［M］．北京:科學出版社，2009．

【6】樸聖炫．應用實驗計畫法［M］．首爾:民英社，1990．

【7】何曉群，劉文卿．應用回歸分析［M］．北京:中國人民大學出版社，2011．