一種基于D-S證據理論的Bayes可靠性評定方法

趙仿澤

?

一種基于D-S證據理論的Bayes可靠性評定方法

趙仿澤

(西北工業大學航海學院, 陜西西安, 710072)

如何合理利用多源先驗信息, 是小子樣Bayes理論方法應用中亟待解決的一個問題。目前, 多源信息融合還沒有統一的準則, 融合理論方法的不同會使得融合結果有所差異。為了解決上述問題, 基于證據推理理論, 提出了一種多源信息先驗分布融合方法, 將通過各種融合準則獲得的先驗分布進行再融合, 得到了一種合理的綜合先驗分布, 最后建立了基于證據理論的Bayes可靠性評定模型。仿真結果表明, 該融合方法是合理可行的, 相比使用單一信息融合方法更科學且合理。

Bayes理論; 多源信息; D-S證據推理; 信息融合; 可靠性評定

0 引言

由于武器裝備受到研制周期和研制經費的制約, 系統可靠性試驗數量很少, 甚至不做系統試驗, 具有典型的小子樣復雜系統特點。但武器裝備在研制過程中, 由于采用高新技術, 以及試驗中設備和手段的進步和多樣化, 使試驗信息具有多種信息源。另外, 在進行系統可靠性評估時又存在大量的試驗信息。從信息論的角度來看, 只有充分利用這些信息, 才能對復雜系統的可靠性有較深刻的認識。

伴隨著Bayes理論的興起, 小子樣試驗分析方法也得到了長足發展。Bayes方法是一種充分利用先驗信息的試驗評估方法, 可大大減少所需試驗子樣數, 節約試驗成本, 提高試驗效率。在利用Bayes理論進行可靠性評定的過程中, 為了盡可能少做現場試驗, 必須充分利用各種先驗信息, 但如何合理利用這些多源先驗信息, 是小子樣理論方法應用中亟待解決的一個問題。

在目前的實際工程應用中, Bayes理論多源信息融合還沒有統一的準則, 不同的學者往往會采用不同的融合準則, 由于采用的理論方法不同, 必定會使得信息融合的結果有所差異。基于此, 本文采用證據推理理論, 提出一種適用于Bayes評估的多源信息先驗分布融合方法, 將通過各種融合準則獲得的先驗信息進行再融合, 得到一種合理的綜合先驗分布。

1 證據推理基本理論

(2)

(4)

其中

(6)

該公式是D-S證據理論的核心, 通過它可以把若干條獨立的證據結合起來, 它滿足交換律和結合律。

2 基于證據推理的Bayes可靠性評定方法

對于復雜系統, 可以獲得各種試驗信息, 目前, Bayes理論多源信息融合還沒有統一的準則, 由于不同的融合準則采用的理論與方法不同, 必定會使得信息融合的結果有所差異, 為此, 本文基于證據推理理論, 將采用各種融合準則獲得的先驗信息進行再融合。

(8)

采用Dempster規則將mass矩陣中的個mass函數綜合為一個統一的mass函數。把前個信息源定義為集合,, 矩陣中前行的個mass函數按Dempster規則產生的綜合mass函數記為

(11)

(13)

(15)

這個mass函數即為證據理論模型的輸出,即先驗分布的融合權重為

由此可得融合先驗分布為

(17)

通過式(11)獲得的后驗分布就可進行可靠性分析。具體評定原理如圖1所示。

3 實例仿真與分析

為驗證所建立的評定模型, 引入文獻[9]的算例進行分析。已知現場樣本數據服從正態分布, 其中, 而未知, 需要通過試驗數據確定其取值。為了說明試驗數據融合的應用及其合理、有效性, 通過計算機產生一組隨機數(其分布為),(5.1139, 6.0668, 5.0593, 4.9044, 4.1677), 相當于實際系統進行了5次現場試驗得到的數據。同時, 假設通過歷史數據得到的關于未知參數的先驗信息數據,(5.020 9, 4.829 7, 5.521 6)(由分布為隨機產生),(5.6961, 5.2431, 6.0791)(由分布為隨機產生)。下面用本文提出的基于證據推理理論融合方法進行分析。

這樣可以獲得融合準則的mass矩陣

(20)

由式(10)~式(13), 得

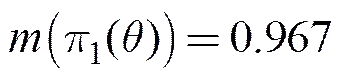
(22)

由此可獲得融合后的先驗分布為

(24)

根據后驗分布, 其對應點估計為5.0385, 非常接近參數的真值5。這足以證明本文方法的有效性和合理性。通過示例也可看出, 該融合方法簡便易行, 因而在可靠性試驗分析等工程研究領域具有良好的應用前景和推廣價值。

4 結束語

本文主要考慮Bayes理論在進行小子樣產品可靠性評定時, 需要充分利用各種先驗信息。目前, 多源信息融合還沒有統一的準則, 融合理論方法的不同會使得融合結果有所差異。本文基于證據推理理論, 提出一種多源信息先驗分布融合方法, 將通過各種融合準則獲得的先驗信息進行再融合, 得到一種合理的綜合先驗分布, 相比使用單一信息融合方法更科學、合理。本文提出的方法可從該方法理論分析可知, 融合的關鍵是不同先驗分布的加權融合。因此, 本文提出的融合方法適用的條件是先驗分布具有線性可加性。因為, 對于某些不具有線性可加性的分布, 一般融合分布是不容易求出的, 使用起來也不一定方便, 這時可以采用近似分布(即統計量的漸進分布), 但會影響融合的效果。本文所建立的方法模型僅通過理論仿真進行了驗證, 尚未得到工程應用。在后續的研究中, 將進一步結合工程研制過程中獲得的數據開展分析。

[1] Aggarwal, Priyanka. Bayes Predictor of One-parameter Exponential Family Type Population Mean Under Balanced Loss Function[J]. Communications in Statistics Theory and Methods, 2006, 35(8): 1397-1408.

[2] Ali H A, El-Desouky A I, Saleh A I. A Novel Strategy for a Vertical Web Page Classifier Based on Continuous Learning Naive Bayes Algorithm[J]. International Journal of Computers and Applications, 2007, 29(3): 259-277.

[3] 張金槐, 唐雪梅．Bayes方法[M]．長沙: 國防科技大學出版社, 1990.

[4] 柴哲麗, 林佳齊, 朱金平．基于貝葉斯的軟件可靠性評估研究[J]．計算機工程, 2010, 36(2): 73-77. Chai Zhe-li, Lin Jia-qi, Zhu Jin-ping. Research on Software Reliability Evaluation Based on Bayes[J]. Computer Engineering, 2010, 36(2): 73-77.

[5] 張士峰, 蔡洪．Bayes分析中的多源信息融合問題[J]．系統仿真學報, 2000, 12(1): 54-56.Zhang Shi-feng, Cai Hong. Fusion of Information of Multiple Sources in Bayesian Analysis[J]. Journal of System Simulation, 2000, 12(1): 54-56.

[6] 張湘平．小子樣統計推斷與融合理論在武器系統評估中的應用研究[D]．長沙: 國防科學技術大學, 2003.

[7] 馮靜, 周經倫, 孫權．Bayes分析中多源驗前信息融合的ML_II方法[J]．數學的實踐與認識, 2006, 36(6): 142-145.Feng Jing, Zhou Jing-lun, Sun Quan. Fusion of Information of Multiple Sources Based on ML-II Theory in Bayesian Analysis[J]. Mathematics in Practice and Theory, 2006, 36(6): 142-145.

[8] 楊春, 李祖懷．一個證據理論模型及其在專家意見綜合中的應用[J]. 系統工程理論與實踐, 2001, 21(4): 43-48. Yang Chun, Li Zu-huai. An Evidence Reasoning Model with Its Application to Expert Opinions Combination[J]. Systems Engineering-Theory & Practice, 2001, 21(4): 43-48.

[9] 馮靜．小子樣復雜系統可靠性信息融合方法與應用研究[D]. 長沙: 國防科學技術大學, 2004.

(責任編輯: 陳 曦)

A Bayesian Reliability Evaluation Method Based on Dempster-Shafer Evidence Theory

ZHAO Fang-ze

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

Bayesian method is an important and suitable approach for system reliability evaluation in small sample circumstance. In order to reduce the testing data, all kinds of a priori information must be used, so the information fusion of multiple sources becomes a key problem in Bayesian analysis. A new method based on the Dempster-Shafer evidence theory is proposed to realize the information fusion of multiple sources, which can integrate more a priori distributions obtained through different fusion criteria. Simulation shows that the proposed method is effective.

Bayesian theory; information of multiple sources; Dempster-Shafer evidence theory; information fusion; reliability evaluation

TJ.630.1; TB114.3

A

1673-1948(2013)03-0175-04

2013-01-29;

2013-03-27.

趙仿澤(1964-), 男, 在讀博士, 主要研究領域為系統工程理論與方法.