一種凸多邊形的爆破網絡等時線算法研究

鄭 武，王 磊，呂仁輝

(武漢科技大學計算機科學與技術學院，湖北武漢430081)

1 問題的提出

在爆破工程中，為了精確控制爆破過程，通常需要借助等時線來分析爆破的趨勢［1］，通過將起爆時刻相同或相近的炮孔用等時線連接起來，就可以更加直觀地看到爆破的進度，而且可以根據等時線進一步確定整個爆破的延伸方向。在實際中，通常是先計算出每個炮孔的起爆時刻，然后統計出起爆時刻相同或相近的炮孔，最后分析爆破的趨勢。某爆破項目的示意圖如圖1，其中數字代表起爆時刻，有箭頭的線段代表孔外延時，沒有箭頭的曲線代表等時線，紅色實心小三角形指明了爆破的巖石移動方向。CHI Bao-ming［2］，ZHANG Wei［3］等學者對針對爆破網絡設計中的等時線進行了相關研究和探討。研究者們提出的等時線算法，針對布孔比較規律的情況下比較有效，但卻有不同延時時間的等時線會存在交叉，獲取等時線時間過長等問題［1-3］。

爆破網絡等時線的生成與優化問題描述如下:在給定的爆破網絡中，所有炮孔的起爆時刻已知，炮孔的位置已知，需要將起爆時刻相同(或近似相同)的炮孔用等時線連起來。要求生成的等時線至少滿足4個條件:

(1)同一等時線不會自相交叉;

(2)等時線簡明直觀，路徑較短;

(3)等時線能自動適應網絡變化;

(4)等時線生成效率較高。

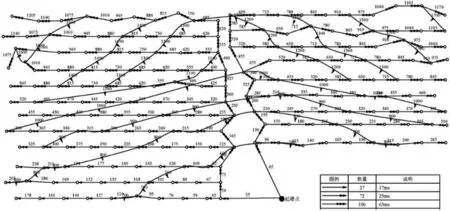
圖1 某工程爆破網絡示意圖

為了更詳細地說明問題，將工程爆破中的相關術語及算法問題形式化描述如下:

定義1 起爆時刻，即爆破工程中炮孔實際起爆的時刻。爆破網絡給定之后，每個炮孔的起爆時刻是客觀存在的。起爆時刻可以根據爆破網絡中的炮孔布局計算得出。

定義2 等時線，即爆破工程中，為了準確直觀地分析爆破過程，將起爆時刻相同(或近似相同)的炮孔連接起來的線。

本文通篇都涉及到等時線一詞，包括等時線的定義、計算、生成、優化等，等時線的形式化定義如下:

定義 Xi、Xj為兩個不同的炮孔，t(Xi)、t(Xj)是炮孔的起爆時刻，Δt是允許的時間間隔。

若│t(Xi)-t(Xj)│≤Δt，則稱 Xi、Xj等時，采用等時線連接;

若│t(Xi)-t(Xj)│ ＞ Δt，則稱 Xi、Xj不等時，不用等時線連接;

其中 1≤i≤n，1≤j≤n。

嚴格按照前文所述的算法要求來完成算法的實現。為了避免同一等時線的交叉問題，采用凸多邊形算法進行等時線的連接。為了使得生成的等時線路徑較短，采用自定義三角形算法進行比較，并采用貪心算法進行優化。具體分為如下幾個過程:

(1)將爆破網絡中的炮孔按照起爆時刻進行分類。

(2)將同一起爆時刻段的炮孔按層次劃分，主要采用凸多邊形生成算法進行歸類。

(3)將同一起爆時刻段上的炮孔按照上一步劃分的層次，初步形成等時線。過程如下:已知最外層的凸多邊形，形成一個回路。首先將次外層的凸多邊形上的各個頂點插入到回路中去，插入時選取插入后使得路徑最短的動作來做。然后按照從外到內的順序依次將各個凸多邊形上的頂點插入到回路中去。文中采用一種三角形方法來快速選擇優先插入的炮孔。

(4)判斷形成的等時線是否存在自相交叉情況，如果存在則進行去交叉算法。

(5)使用貪心算法進一步優化等時線。

2 算法描述

在實際的爆破工程中，一般會用到大量的炮孔，炮孔的位置是根據爆破的需要而分配，炮孔的起爆時刻也不全相同。在統計完炮孔的起爆時刻后，會發現同一起爆時刻的炮孔位置很散亂的分布，這時如何將各個起爆時刻相同的炮孔連成一條等時線呢?使用相鄰連接的辦法經常會造成連線的交叉、相鄰的距離很遠等缺陷，為了避免這些問題，我們需要采用一種新的等時線生成算法——基于凸多邊形的插入算法。為了盡可能詳細的說明這一算法，本文只討論一條等時線的生成，基本模型如圖2。給定一些均勻分布的炮孔，這些炮孔的起爆時刻相同或近似相同，每個炮孔的位置已知，要求把這些炮孔連成一條等時線。圖2中所有炮孔的起爆時刻相同或近似相同，炮孔的位置是均勻隨機分布的。

圖2 均勻分布的100個炮孔

2.1 按層次劃分炮孔

第1步 在圖2所示的區域里搜索出以炮孔位置為頂點的最外層的凸多邊形，標記這個凸多邊形上的炮孔，并標記這個凸多邊形為0層(搜索凸多邊形可以參考 Graham＇s Scan 算法)［4］;

第2步 在剩余沒有被標記的炮孔中搜索以炮孔位置為頂點的最外層的凸多邊形，標記這個凸多邊形上的炮孔，并標記這個凸多邊形為第1層。

……重復第2步的操作，直到剩余的沒有標記的炮孔位置不足以構成一個凸多邊形。

在執行完所有的步驟之后，原來沒有規律的炮孔已經被按層次分開了，如圖3。

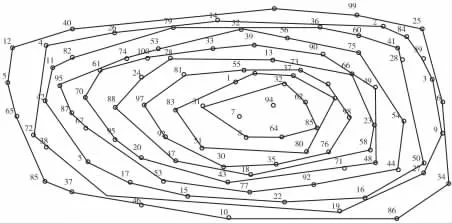
圖3 搜索所有的凸多邊形

2.2 炮孔分層插入

在找到所有的凸多邊形后，對這些凸多邊形進行編號，從最外層到最內層依次為第0層，第1層，第2層，……，第n層(注意，如果最里面有不在凸多邊形上的炮孔，那么把這些炮孔記作最內層上的，即第n層)。

插入過程如下:

第1步 將第1層上所有的炮孔依次插入到第0層，執行完之后第1層為空，第0層上新增加了原來第1層所有的炮孔;

第2步 將第2層上所有的炮孔依次插入到第0層，執行完之后第2層為空，第0層上新增加了原來第2層所有的炮孔;

……重復第2步的操作;

第n步 將第n層上所有的炮孔依次插入到第0層，執行完之后第n層為空，所有的炮孔都被添加到第0層上，即當前只有一層。

為了保證最終形成的等時線最短，沒有交叉，就需要確定最優的插入算法。具體的過程是將待插入的炮孔在每個能夠插入的位置進行一次插入操作，而最終選擇執行完插入操作后總路徑最短的插入方法，具體的插入過程分成兩步。

2.2.1 插入位置選擇

算法如圖4。炮孔p0有兩個插入位置可以選擇(p1與p2之間，p2與p3之間)，采用算法1之后增加的長度為Δs1=a1+b1-c1;采用算法2之后增加的長度為Δs2=a2+b2-c2;比較Δs1和Δs2的大小，選擇其中較小的插入算法。

圖4 算法及效果示意圖

2.2.2 插入炮孔的順序選擇

選擇先插入點示意圖如圖5。有p01，p02兩個炮孔需要被插入到等時線上，那么如何確定哪個炮孔先插入進去呢?做法是先按照步驟1對p01，p02分別選出最優的插入位置，然后選出完成插入操作后路徑最短的炮孔，則這個炮孔就被選擇優先插入。

2.2.3 優化——去交叉

在完成上述操作后，基本上可以生成滿足要求的等時線。經測試，上述方法在中等規模數量(150個炮孔左右)下沒有問題，但是在炮孔數量龐大(200個以上)的情況下，偶爾會出現一兩處交叉情況，如圖6(a)。經過反復試驗發現，出現交叉情況只會在少數情況而且在很小區域里，采用貪心算法矯正這部分的交叉即可(如圖6(b))。

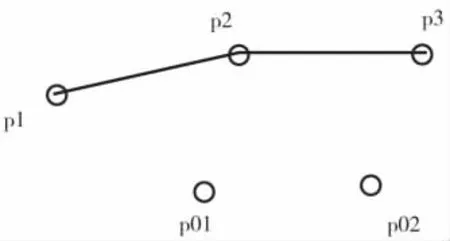
圖5 選擇先插入點示意圖

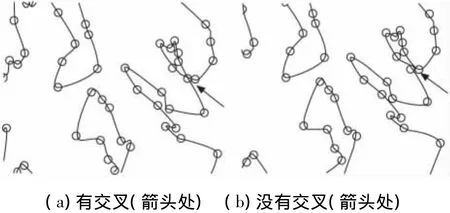
圖6 交叉情況示意圖

矯正交叉過程如圖7。p1-p4與p2-p5出現交叉情況如圖7(a)，只要將p1連到p2，p4連到p5即可消除交叉，如圖7(b)。

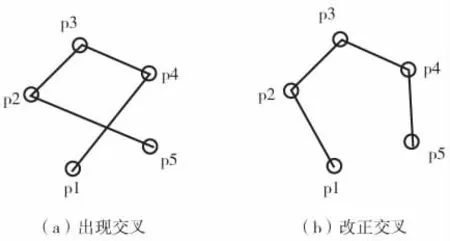
圖7 矯正交叉過程圖

3 測試結果

本程序的運行測試是在Windows7 32位操作系統上進行的，處理器是Intel CORE2 2.20 GHz，安裝內存為2.00 GB。

對本文的算法進行了兩方面的檢測，首先用自動生成的大量炮孔進行檢測，然后用實際爆破工程圖進行檢測。在采用自動生成的炮孔檢測時，采用200個炮孔進行10次檢測，發現生成的等時線符合要求，生成速度較快。在采用實際工程案例測試時，采用了10個規范布局圖進行檢測，發現生成的等時線滿足工程要求。同時實際項目中等時線所花時間比均勻隨機布孔花的時間少得多，主要是因為實際項目有多條等時線，每條等時線上的炮孔的數量較少造成的。具體測試數據見表1和表2。

表1 均勻隨機分布炮孔測試結果

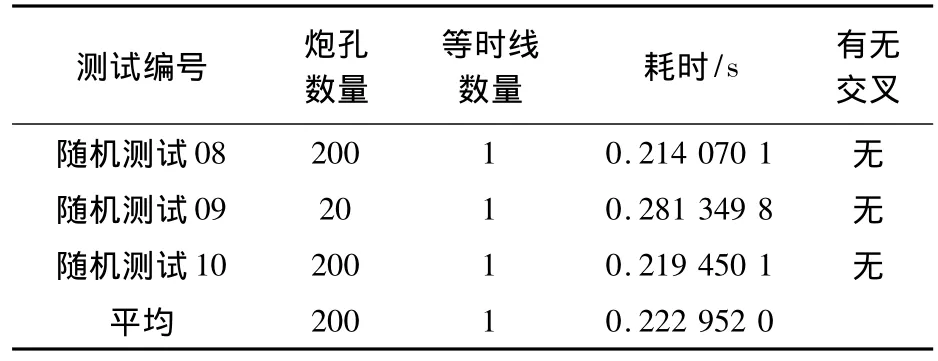
續表

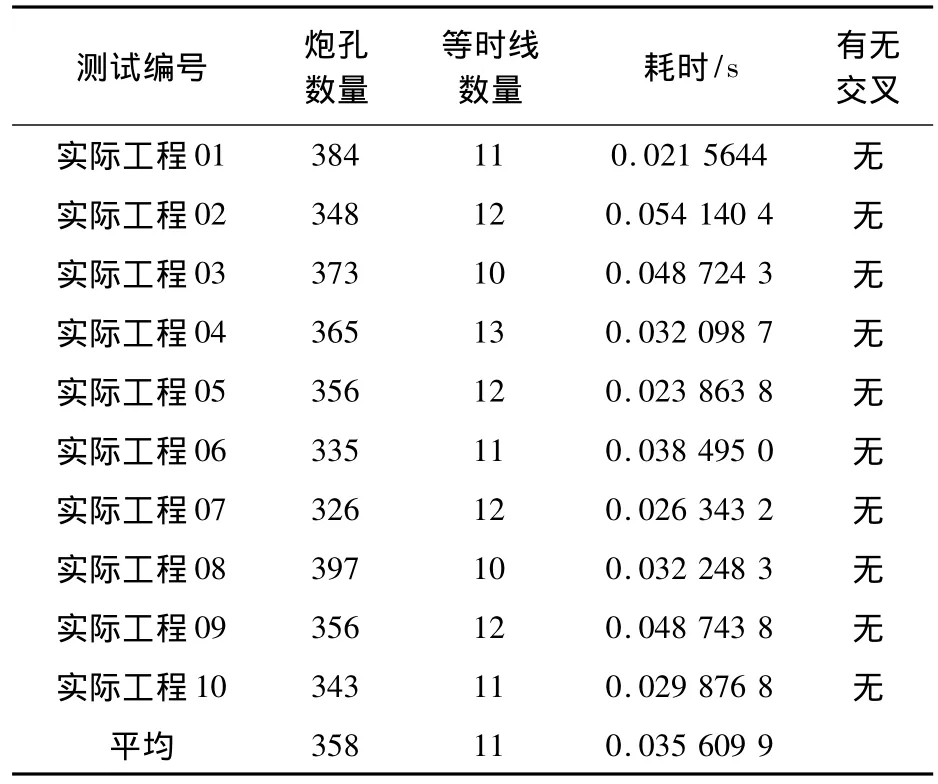
表2 實際工程案例測試結果

4 結語

本文主要探討了基于凸多邊形插入的爆破網絡等時線的生成及優化算法，通過分層插入的方法使復雜的爆破網絡具有清晰的層次，并且有條理地將每一個炮孔插入到相應的等時線上，最后說明了插入過程中的問題及解決方案。通過具體的實驗證明，該算法可以適用于復雜網絡情況的等時線生成，并且可以達到較好的效果。

［1］張樂，顏景龍.起爆延期等時線的生成及其應用研究［J］.工程爆破，2010，16(2):86-90.

［2］CHI Baoming，LI Zhijun，YE Yong.Study on the arithmetic of automatically drawing isoclines of groundwater level based on GIS［J］.Journal of Jilin University(Earth Science Edition)，2007，37(2):261-265.

［3］ZHANG Weiqin，QING Yan ，JIAN Xingxiang.Natural neighbor interpolation and its application to 2D grid of irregular data［J］.Computing Techniques for Geophysical and Geochemical Exploration，2011，6(3):291-295.

［4］RONALD L G.An efficient algorithm for determining the convex hull of a finite planer set［J］.Information Processing Letters，1972，1(1):132-133.