基于人工蜂群支持向量機的模擬電路故障診斷

曾 濤，趙 嵐

(1.燕山大學信息化處，河北 秦皇島 066004;2.秦皇島職業技術學院 機電工程系，河北 秦皇島 066004)

0 引言

20世紀90年代，Vapnik等在統計學習理論(SLT)的基礎上提出一種新型機器學習方法——支持向量機 (Support Vector Machine，SVM)。與神經網絡等學習方法相比，支持向量機基于結構風險最小化原則，具有小樣本學習、泛化能力強等特點，能有效地避免過學習、局部極小點以及“維數災難”等問題[1，2]。目前，SVM 的實用算法研究、設計和實現都已取得了豐碩的成果，并且廣泛應用于故障診斷、數據挖掘、文本識別[3]等領域。但是支持向量機的參數選擇決定了其學習性能和泛化能力，由于在參數的選擇范圍內可選擇的數量是無窮的，在多個參數中盲目搜索最優參數是需要極大的時間代價，并且很難逼近最優。針對支持向量機的參數選擇問題，很多學者進行了大量的研究，文獻[4]在分析了幾種評估SVM性能的方法之后，利用梯度下降法對SVM參數進行優化，取得了較好的效果，但是梯度下降法容易陷入局部極小值。文獻[5]利用Bootstrap方法建立的支持向量機的評估函數，利用模擬退火算法對參數進行了優化。文獻[6，7]分別利用蟻群優化算法與小生境遺傳算法對SVM核參數進行優化，都取得了較好的結果。

蜂群算法是建立在蜜蜂自組織模型和群體智能基礎上的一種非數值優化計算方法[8]。文獻[9]對蜂群算法在解決組合優化問題中的原理和應用方法，并將其應用于旅行商問題 (TSP)等問題。本文將人工蜂群算法應用于支持向量機的參數優化當中，對其應用方法進行了詳細的闡述，并利用UCI數據庫中的數據對其進行了仿真，最終將其用于模擬電路故障診斷當中，取得了較好的效果。

1 支持向量機及其參數分析

1.1 支持向量機

支持向量機就是尋找一個最優分類超平面，即最大間隔超平面。訓練集為非線性時，通過一個非線性函數φ(x)將訓練集數據x映射到一個高維線性特征空間，在這個維數可能為無窮大的線性空間中構造最優分類超平面，并得到分類器的決策函數。

對于二類分類情況，訓練樣本集為

為了找到最優超平面，必須求解下列二次優化問題:

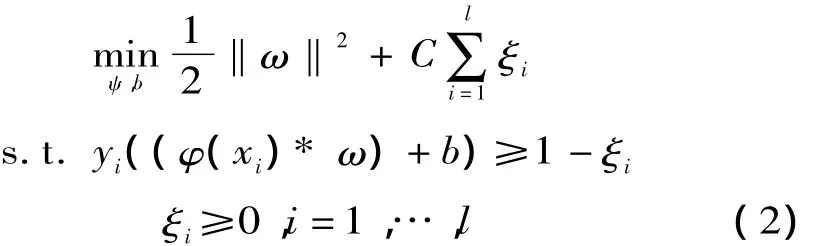
式中:*表示內積;ω為系數向量;ξi≥0為考慮到存在一些樣本不能被正確分類，為了保證分類的正確性，而引入的松弛變量;C稱為懲罰因子，通過改變懲罰因子可以在分類器的泛化能力和誤分類率之間進行折衷。

其對偶問題為一個凸二次規劃問題，具有全局最優解，從而避免了局部極小點的問題。

最終可以得到決策函數:

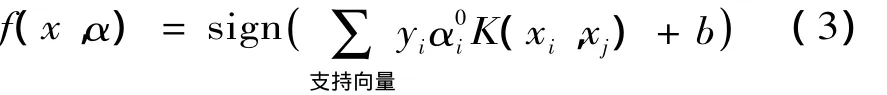
構造這一類決策函數的學習機器稱為支持向量機。支持向量機的結構示意圖如圖1所示[10]。

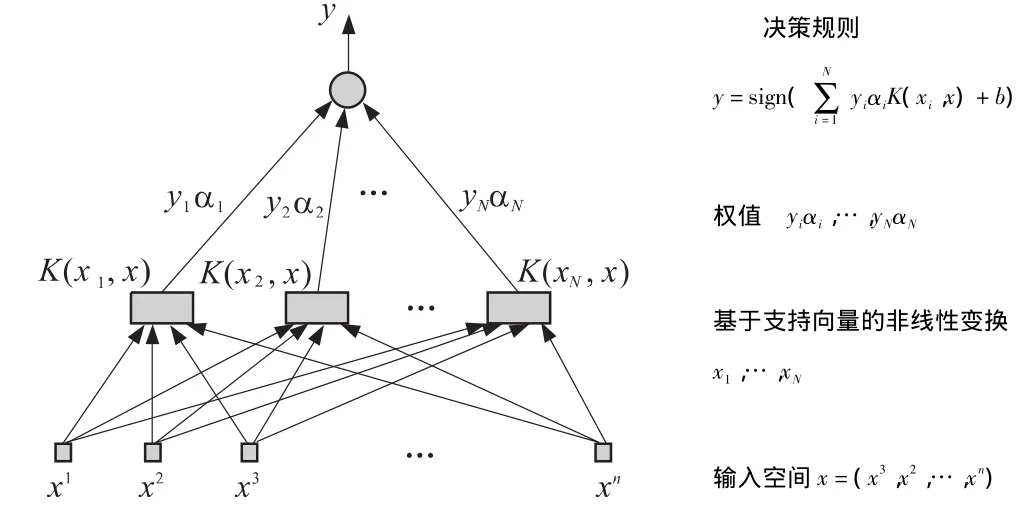
圖1 支持向量機結構圖Fig.1 Structure block of support vector machine

1.2 參數分析

支持向量機的性能依賴于多個參數，其中懲罰因子C，控制間隔的最大化與分類誤差之間的折衷，C越大，則對于錯分樣本的懲罰越大。其他的參數出現在非線性映射函數中的核參數，影響樣本在高維特征空間的分布情況，如RBF函數中的γ，核參數的改變實際上隱含著改變了映射函數，即改變了特征空間的VC維，從而影響置信范圍，最終影響結構風險范圍。為了簡單，將它們統稱為核參數，這樣就可以將它們在一個統一的框架內處理。

2 蜂群算法的基本原理

人工蜂群算法 (Artificial Bees Colony，ABC)是近年來根據自然界密封群體的搜集食物，即采蜜過程的模擬而提出的一種群算法。蜂群采蜜行為主要包括3個基本部分:蜜源、采蜜蜂、待工蜂。此外引入3種基本的行為模式:搜索蜜源、為蜜源招募和放棄蜜源。

(1)蜜源。蜜源代表各種可能的解。

(2)采蜜蜂。采蜜蜂攜帶了具體的蜜源信息，這些信息包括蜜源與蜂巢的距離、蜜源方向、蜜源的收益度;采蜜蜂通過搖擺舞與其他蜜蜂分享這些信息，按一定比例，部分成為引領蜂。

(3)待工蜂。待工蜂可以分為偵查蜂、跟隨蜂。偵查蜂搜索蜂巢附件的新蜜源。跟隨蜂在蜂巢內等待，通過分享采蜜蜂的信息，尋找蜜源。開始時，待工蜂沒有蜂巢附近蜜源的信息，因此有兩種選擇:(a)待工蜂可以作為偵察蜂，由于某一內部激勵或可能的外在因素，開始自發地搜尋在蜂巢附近的蜜源。(b)在觀察到其他蜜蜂搖擺舞后，它可被招募并按照獲得的信息尋找蜜源。待工蜂發現新的蜜源后，記住蜜源的位置，并迅速開始采蜜，此時，待工蜂變成了采蜜蜂。蜜蜂采蜜回到蜂箱卸蜂后，有以下幾種選擇:(a)放棄蜜源，成為待工的跟隨蜂;(b)返回同一蜜源前，跳搖擺舞招募蜂巢其他伙伴。(c)不招募其他蜜蜂，繼續采蜜。初始時刻，蜜蜂均無任何先驗知識，都是偵察蜂。隨機搜索到食物源后，偵察蜂返回蜂巢的舞蹈區，根據食物源收益度的相對大小，偵察蜂可以轉變為上述任何一種蜜蜂，原則如下:

(1)所采集食物源的收益度相對很低時，它可以再次成為偵察蜂搜尋附近的食物源。其轉變結果是放棄上次采集的食物源。

(2)所采集食物源的收益度排名小于臨界值(如排名在后50%)時，它可以在觀察完舞蹈后成為跟隨蜂，并前往相應的食物源采蜜。

(3)所采集食物源的收益度排名高于臨界值時，它成為引領蜂，繼續在同一食物源采蜜，并在舞蹈區招募更多的蜜蜂采集相應食物源。

3 基于人工蜂群優化算法的SVM參數選擇

ABC算法正是受此啟發，該算法基本思路如下:在循環開始時，所有的人工蜂均在蜂巢。在搜索過程中每個人工蜂都做局部的搜索，從而逐步增加可行解。在每一步的搜索過程中，其中的一個或者多個最優解都被保存下來，最終通過決策分析得到最優解。根據人工蜂群算法和支持向量機參數尋優的特點，其基本思路如下:

Step 1:確定人工蜂群的群體數量，即蜂群中蜜蜂總數，設為B。確定偵查蜂占群體數量的比例，一般大于10%，易于收斂，偵查蜂數量為SN。

Step 2:開始時刻，所有蜜蜂均成為偵查蜂，在給定范圍內隨機確定B個蜜源，即隨機選擇B個 (C，γ)的組合參數。

Step 3:計算這B個蜜源的品質，初始蜜源的品質由其單點的分類準確率決定。對于蜜源品質低的情況，偵查蜂可以繼續作為偵查蜂繼續搜索蜜源，也可以作為跟隨蜂去較高品質的蜜源進行采蜜;根據蜜源品質，跟隨蜂按照一定的比例跟隨到各個蜜源進行采蜜。

Step 4:跟隨蜂到達各個蜜源后，在蜜源附近的連續區域進行采蜜，以確定在這一蜜源的最優品質點。其中蜜源附近各個蜜源點的確定方式采用下式確定:

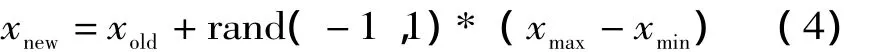
式中:xmax和xmin決定了要搜索的蜜源區域范圍。

Step 5:蜂群回到蜂巢后，計算各個蜜源的品質，重新分配各個蜜源的采蜜蜂數量。計算蜜源品質的方法:a.蜜源中最好的品質點，即其中最優的分類準確率;b.蜜源區域所得的品質平均值，即所有分類準確率的平均值。

循環上述步驟，最終得到最優的蜜源點，即得到最優的SVM參數。

4 仿真及分析

首先，利用 UCI[11]數據庫中的 Ionosphere，Haberman，Dermatology和Vehicle數據對本方法進行仿真驗證。其中核函數選擇RBF核函數，即需要選擇的核參數位懲罰參數C和寬度參數γ。在Matlab環境下對其進行仿真。人工蜂群的參數選擇如下:蜂群數量為100，偵查蜂的比例為20%。文中同時利用網格搜索的方式進行參數的搜索，以和人工蜂群搜索結果進行對比，其中參數范圍選擇為 C=(2-5，2-4，…，28)，γ =(2-5，2-4，…，25)。最終仿真結果如表1所示。

表1 UCI數據仿真結果Tab.1 Simulation results of UCI data

由仿真結果表明，人工蜂群算法相對于網格搜索的方法能夠較好地對支持向量機參數進行優化。

將人工蜂群優化參數的支持向量機用于模擬電路的故障診斷。本文采用ITC’97[12]中的Elliptical濾波器標準電路對本文方法進行仿真驗證。圖2所示為文中用到的Elliptical濾波器電路原理圖。表2所示為電路中各個元器件的標稱值。在Pspice環境下對電路進行正常狀態和故障狀態的仿真。表3給出了設置故障的方式，這里均采用原件的軟故障，即元器件標稱值上升或下降50%。

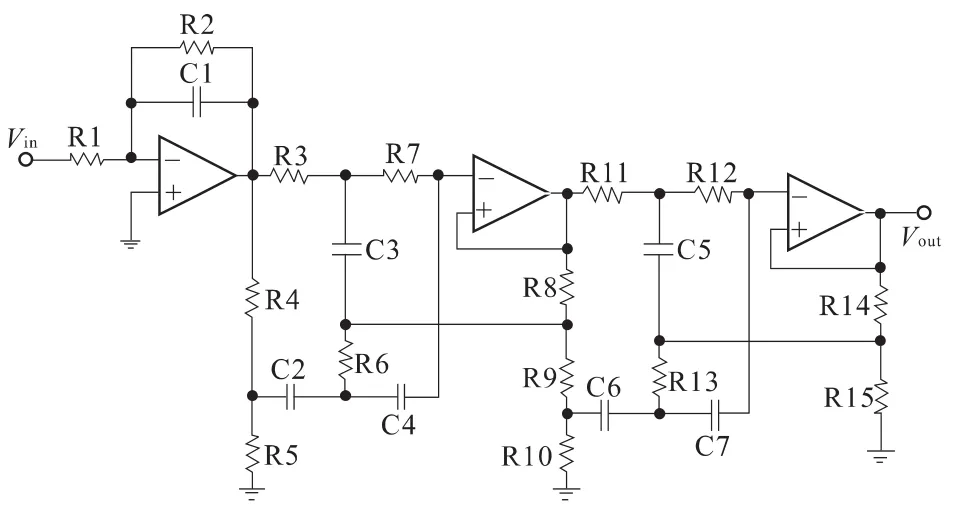
圖2 Elliptical濾波器原理圖Fig.2 Schematic diagram of Elliptical filter

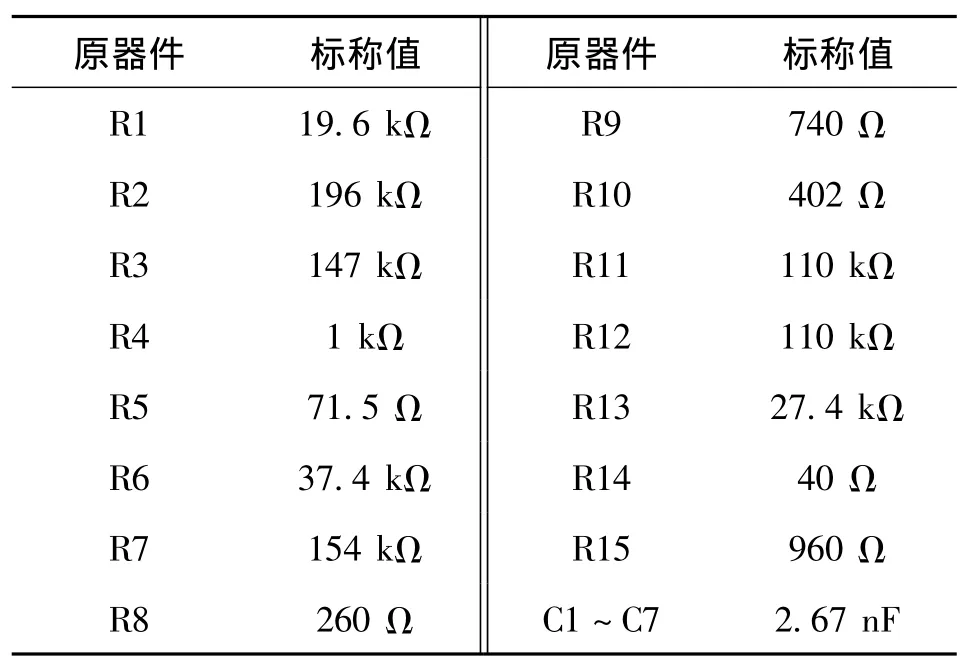
表2 元器件標稱值Tab.2 Nominal value of components

表3 電路故障設置方式Tab.3 Setting mode of circuit fault

對電路正常狀態和所有設置故障狀態進行30次Monte-Carlo分析，得到輸出信號。這里采用3個運放的輸出信號作為故障診斷信號。對采集信號進行小波變換以進行特征提取，利用信號的各頻段的頻譜能量作為診斷特征進行診斷。通過小波特征提取，得到330個樣本，每類30個樣本，這里利用每類中的20個樣本訓練，另外10個樣本作為驗證樣本。

利用ABC-SVM對電路得到的特征樣本進行訓練和驗證。仿真結果如下:C=95.616 9，γ=0.796 7，分類準確率達到99.09%。以上結果表明，基于人工蜂群算法優化參數的支持向量機能夠較好地實現對模擬電路的故障診斷。

5 結論

針對支持向量機中的參數優化問題，本文引入了人工蜂群算法。利用人工蜂群算法的全局優化特性對支持向量機的參數進行了有效的選擇。最終將人工蜂群支持向量機用于模擬電路故障診斷，有效得到了故障分類器的最優參數，從而提高了模擬電路故障診斷準確率。但是本文中只是利用人工蜂群算法對支持向量機的參數進行了選擇，由于參數和特征選擇是密切相關的，因此對其進行聯合優化是以后的研究方向。

[1]張倩，楊耀權.基于支持向量機核函數的研究[J].電力科學與工程，2012，25(5):42-45.Zhang Qian，Yang Yaoquan.Research on the kernel function of support vector machine[J].Power Science and Engineering，2012，25(5):42-45.

[2]祖文超，李紅君，苑津莎.基于糾錯能力的SVM在變壓器故障診斷的應用[J].電力科學與工程，2012，28(11):39-43.Zu Wenchao，Li Hongjun，Yuan Jinsha.Application of transformer fault diagnosis based on the error-correcting codes capability of SVM[J].Power Science and Engineering，2012，28(11):39-43.

[3]Wang T Y，Chiang H M.Fuzzy support vector machine for multi-class text categorization[J].Information Processing and Management，2007，43:914-929.

[4]Chapelle O，Vapnik V，Bousquet O，et al.Choosing multiple parameters for support vector machines[J].Machine Learning，2002，(46):131-159.

[5]趙春秀，周輝仁，劉春霞.基于SA和Bootstrap的LSSVM參數優選及應用[J].統計與決策，2008，(15):25-28.

[6]劉春波，王鮮芳，潘豐.基于蟻群優化算法的支持向量機參數選擇及仿真[J].中南大學學報 (自然科學版)，2008，39(6):1309-1313.Liu Chunbo，Wang Xianfang，Pan Feng.Parameters selection and stimulation of support vector machines based on ant colony optimization algorithm[J].Journal of Central South University(Science and Technology)，2008，39(6):1309-1313.

[7]朱寧，馮志剛，王祁.基于小生境遺傳算法的支持向量機分類器參數優化[J].南京理工大學學報 (自然科學版)，2009，33(1):16-20.Zhu Ning，Feng Zhigang，Wang Qi.Parameter optimization of support vector machine for classification using niche genetic algorithm[J].Journal of Nanjing University of Science and Technology(Nature Science)，2009，33(1):16-20.

[8]胡中華，趙敏.基于人工蜂群算法的TSP仿真[J].北京理工大學學報，2009，29(11):978-982.Hu Zhonghua，Zhao Min.Simulation on traveling salesman problem(TSP)based on artificial bees colony algorithm[J].Journal of Beijing Institute of Technology，2009，29(11):978-982.

[9]Teodorovic D，Lucic P，Markovic G，Dell'Orco M.Bee colony optimization:principles and applications[C]，2006:151-156.

[10]Vapnik.統計學習理論[M].許建華，張學工譯.北京:電子工業出版社，2004.

[11]Blake C L，Merz C J.UCI repository of machine learning databases.Univ.Clifornia，Dept.Inform.Comput.Sci.，Irvine，1998.

[12]Kondagunturi R，Bradley E，Maggard K，et al.Benchmark circuits for analog and mixed-signal testing[C].1999.