基于GSC框架降秩自適應濾波算法研究

羅 熹， 李 宏， 姜嘉琳

（1.西北工業大學，電子信息學院，陜西 西安 710072；2.西安電子科技大學 電子工程學院，陜西 西安 710071）

STAP（Space Time Adaptive Processing）即空時自適應處理，由于具有它可在空時兩維對雜波進行抑制和信號積累，有效地改善了動目標檢測的能力，特別是在主瓣雜波區效果尤為明顯，因此受到了廣泛地關注。但由于其龐大的計算量、實現的復雜度以及難以獲得足夠的樣本估計數，使得在保證性能次優的條件下降低計算的復雜程度的降秩算法成為研究的熱點。

目前，基于GSC框架的算法多應用于降低自由度r的方面，由此此方法多應用于多級維納濾波器的有效實現，CDMA中的空時二維中的自適應濾波和用戶檢測，空時雷達設計中的CFAR預警檢測技術，最后GPS干擾抑制算法上也可以運用降秩算法來有效處理輸入和輸出信號。作為一種新的信號處理技術，我們應該多運用其到各個信號處理的階段。文中將圍繞GSC框架的主分量法（Principle components）和交譜法（Cross spectrum method）[2-3]進行研究。 同時，在對 GSC模型優化方面，采用多級維納濾波器（Multistage Wiener Filter）進行后期截斷。分別對上述3種方法進行分析和總結，并得出3種方法之間的關系。

1 陣列模型

考慮一N元均勻間隔線性天線陣，有M個不相關的窄帶信號入射，其中一個為期望信號，（M-1）為干擾信號，則此天線陣在t時刻接收到的信號為:

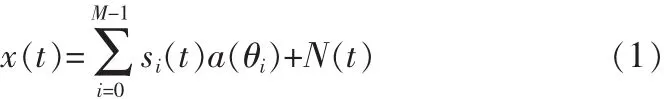
其中 i=0 為期望信號；i=1，…M-1 為干擾信號；si（t）為信號的幅度包絡；a（θi）為信號的方向向量；N（t）為背景噪聲（文中假設為高斯白噪聲）。接收信號的相關矩陣為:

其中H為共軛轉置。

在具體實踐中一般用統計平均來計算相關矩陣，即:

其中K為快拍的次數。

2 基于GSC的一般結構

自適應陣列處理的GSC框架便于把線性約束（甚至靜態方向圖控制）與自適應濾波及其降秩處理分開，在GSC框架下可采用降秩變換的方法進行降秩處理。

圖1為基于框架的降秩變換自適應濾波器的結構，稱為降秩廣義旁瓣相消器 （RR-GSC，Reduced Rank Generalized Sidelobe Canceller）[4-5]。基于框架的降秩變換自適應濾波算法依據降秩變換矩陣的不同，可分為基于特征分解的降秩算法和降秩多級維納濾波器[6]。

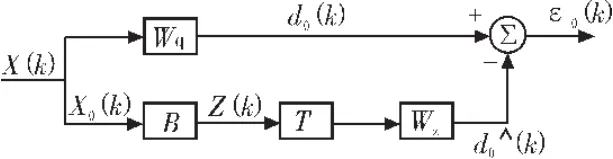
圖1 基于GSC一般降秩處理結構Fig.1 Normal RR processing structure based on GSC

圖1中Wq和B分別為靜態權矢量和阻塞矩陣[7]，其中阻塞矩陣B的意思在于能夠基本消除旁瓣中溢出的干擾。其中：

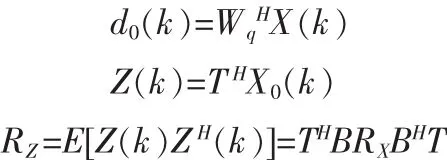
d0（k）和Z（k）看作是維納濾波器的參考信號和輸入信號向量，其推倒結果為:

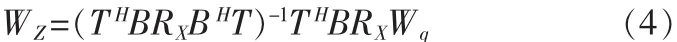
由此可得，GSC框架一般結構權向量:

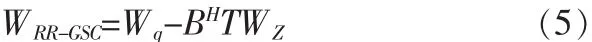
將（4）式代入（5）式可得:

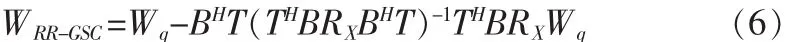
3 GSC框架主分量法（PC）

GSC框架下的降秩變換矩陣由Rx0的特征向量構成，可分為主分量法和交叉譜法，分別記為PC-GSC和CS-GSC，主分量法的核心在于取Rx0中M個大特征值所對應的特征向量來重新構造降秩變換矩陣，Rx0的特征分解為:

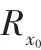
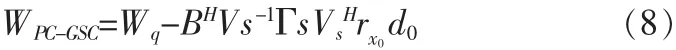
代入主分量法權值得采樣最小均方誤差（SMSE）[8]：

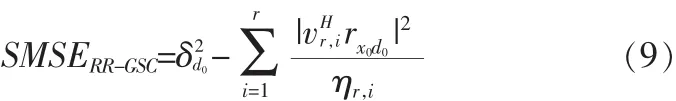
4 GSC框架交叉譜法（CS）

由矩陣分析的知識我們可知，由主分量法（PC-GSC）構造的降秩變換矩陣一定不是最優的，僅僅只是體現了特征分解的速度上的優勢。而我們換個角度，從信干噪（SINR）最大的角度出發，選擇令式（14）指標最大的M個特征值組成降秩變換矩陣，在維數一定的前提下，使得輸出的信干噪比（SINR）最大。利用交叉譜[9-10]可以得到改善的降秩性能。

選取使M個使交叉譜最大的特征向量，即為交叉譜法。

5 降秩多級維納濾波器（RR—MWF）

多級維納濾波器在每一級形成兩個子空間，一個在互相關方向，一個在正交子空間方向。然后互相關向量的正交數據被用同樣的方法再次分解，這種方法在每一級結構都可以減少數據的維數，，從而這種類似金字塔結構的分解結構被作為一個解析濾波器組被重新定義。圖2為多級維納濾波器的結構圖，以4階維納濾波器為例。圖3為4階維納濾波器的等效形式，從圖3中可以看出與圖1基于GSC的一般降秩結構形式完全一致。

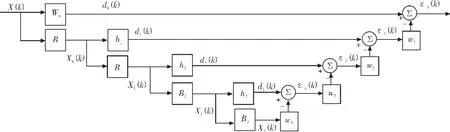
圖2 4階維納濾波器Fig.2 Wiener filtering on 4 rank

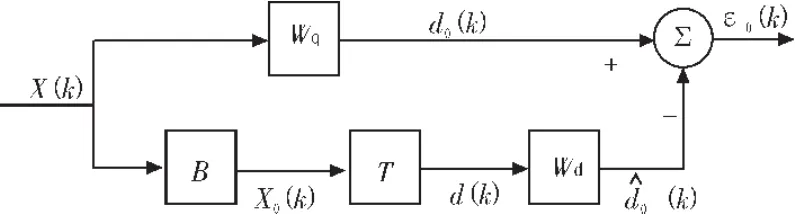
圖3 多級維納濾波器等效形式Fig.3 Equivalent method on MWF

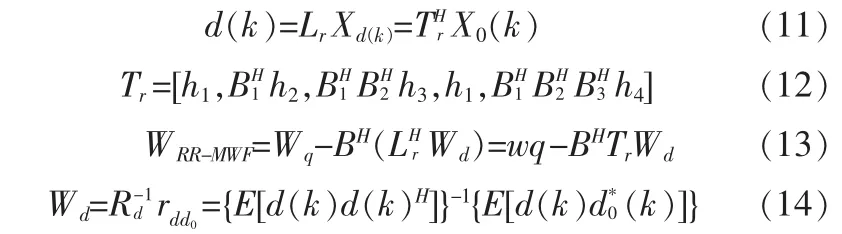
6 算法性能（CSNR）分析

雷達接收機的檢測概率是衡量雷達性能指標最重要的參數之一。檢測概率可以用（Conditional SNR）[11]的函數，CSNR可以用來表示算法中SINR的損失。故CSNR可以定義為算法結果的SINR與期望的SINR的比值：

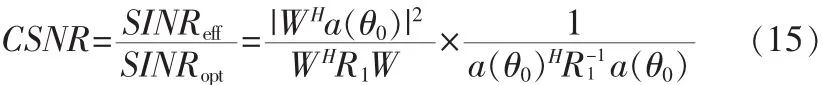
式（15）中R1為干擾加性噪聲協方差矩陣。

對于GSC結構來說，T由接收數據X決定，因為X存在高斯白噪聲，故具有隨機特性，所以很難直接得到CSNR結果，一般只能通過統計分析得到。對于GSC結構來說，SINR的損失主要由于降秩以及利用快拍數估計協方差矩陣所帶來的。后面的仿真能夠說明這個問題。

7 計算機性能仿真

在文中仿真試驗中，假設陣列為均勻直線陣，其中陣列包含有20個陣元，忽略陣元間的耦合因素，陣元間距為半波長，而與加性噪聲不相關。同時假設期望信號為0°方向，3個不相關干擾信號來自55°，-22°，和-45°方向。干擾噪比均為15 dB。取快拍數為200，實驗結果通過1 000次蒙特卡洛實驗平均得到。

但如何比較哪種算法最優。將利用以下兩個指標：采樣最小均方誤差（SMSE）和雷達檢測概率（CSNR）。其中圖4為兩種算法的SMSE比較（其中取以10為底的對數），從圖中可以看出，當秩r<3時PC-GSC和CS-GSC曲線基本一致，但是CS-GSC選擇基向量。

所以其SMSE曲線較之PC-GSC略高。當r=3的時候PC-GSC的曲線開始降低說明其算法的不穩定性。而CSGSC的曲線開始升高說明誤差開始減少，并基本達到最小值。由此說明CS-GSC比PC-GSC的降秩性能更好，穩定性更高，在隨機噪聲的背景下可以很好的體現降秩特性，而且能夠更好的選擇信號本身。

圖5（其中取以10為底的對數）為PC-GSC和CS-GSC兩種算法在接收數據中含有期望信號且干擾和噪聲協方差不可估計的情況下輸出CSNR隨降秩矩陣維數的變化曲線。從圖5中可以看出，當降秩矩陣維數小于3時，即實際干擾個數，CS-GSC的性能優于PC-GSC的CSNR性能。但是當降秩矩陣維數大于3時，PC-GSC的CSNR性能比PC-GSC方法要差。同時，當r=3時，PC-GSC和CS-GSC的CSNR值都達到最大。

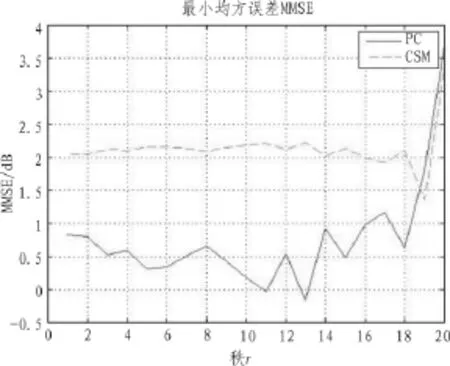
圖4 采樣最小均方誤差（SMSE）Fig.4 Sampling minimum mean square error

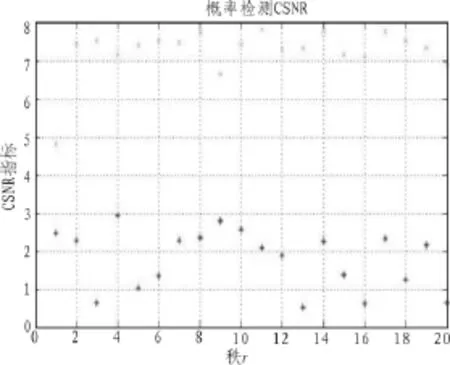
圖5 檢測概率（CSNR）Fig.5 Detection probability

圖6為運用多級維納濾波（MWF）算法，信號降秩前后的對比圖。圖7為多級維納濾波算法的最小均方誤差（MMSE）指標。通過圖6的降秩效果可以看出，MWF算法的降秩效果比基于正交投影算法的PC（主分量法）和CS（交譜法）更好。從圖7（其中CSNR取以10為底的對數）中可得出，當r小于3時，MMSE逐漸減小；當r等于3時為最小；當r大于3時又開始上升。比較3種方法的可以看出算法的效果最好，最接近理想指標。

8 結 論

文中對降秩自適應濾波算法進行了系統的分析和總結，比較了一般GSC結構與主分量法和交叉譜法的關系，以及PC-GSC和CS-GSC相比較于其他GSC結構框架的降秩自適應處理的優勢。同時，介紹了多級維納濾波器（MWF）的原理，并且運用這種原理，對相同的輸入信號，進行降秩處理。通過仿真實驗，比較了上述3種算法的優點與缺點。首先在穩定性和最小均方誤差方面多級維納濾波法優于交叉譜法，而交叉譜法CSNR要優于主分量法，從而提高了降秩處理的效果。其次，通過檢測概率指標表明主分量法和交叉譜法各有各的優勢。當降秩矩陣維數小于實際干擾數目時，交叉譜法性能好于主分量法，但是當降秩矩陣維數大于實際干擾數目時，則情況反之。總之，基于框架GSC的降秩濾波算法可以較為良好的處理線性自由度過多的問題，為雷達信號的后期處理提供了收斂速度更快和計算量大幅降低的結果。

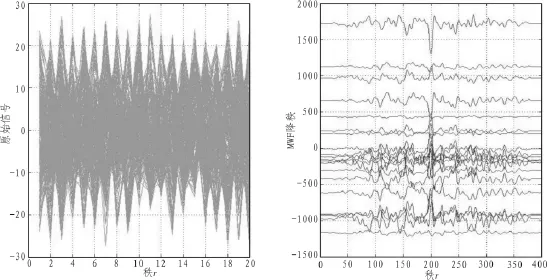
圖6 MWF算法降秩前后效果圖Fig.6 Result picture on using MWF between before and later

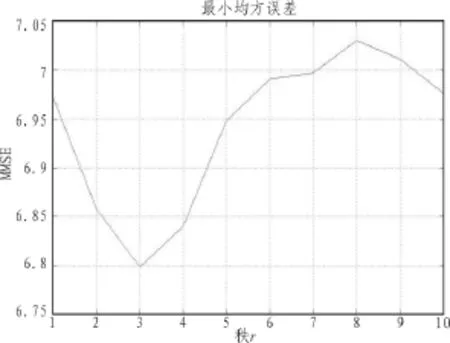
圖7 MWF算法的最小均方誤差Fig.7 Sampling minimum mean square error on MWF

[1]丁前軍，王永良，張永順.自適應陣列處理典型算法的內在關系與統一框架[J].系統工程與電子技術，2006，28（2）:163-170.

DING Qian-jun，WANG Yong-liang，ZHANG Yong-shun.On the relationship between adaptive array processing algorithms and the unified frame[J].Systems Engineering and Electronics，2006，28（2）:163-170.

[2]Haimovich A M.An eigenanalysis interference canceler[J].IEEE Transactions on Signal Processing，1991，39（1）:76-84.

[3]Haimovich A M.The eigencanceler:adaptive radar by eigenanalysis methods[J].IEEE Transactions on Aerospace and Electronics Systems，1996，32（2）:532-542.

[4]Goldstein J S，Reed I S.Reduced-rank adaptive filtering[J].IEEE Transaction on Signal Processing，1997，45（2）:490-496.

[5]Goldstein J S，Reed I S.Subspace selection for partially adaptive sensor array processing[J].IEEE Transaction on Aerospace and Electronics Systems，1997，33（2）:530-544.

[6]丁前軍.降秩自適應波束形成技術研究[D].西安：空軍工程大學，2006.

[7]Goldstein J S，Reed I S，Scharf L L.A multistage representation of the wiener filter based on orthogonal projections[J].IEEE Transactions on Information Theory，1988，44（7）:2943-2959.

[8]Van Veen B D.Eigenstructure based partially adaptive array design[J].IEEE Transaction on Antennas and Propagation，1988，36（3）:357-361

[9]Fa R，De Lamare R C，Zanatta Filho D.Reduced-rank STAP algorithm foradaptive radarbased on jointiterative optimization of adaptive filter[C]//42nd Asilomar Conference on Signal， Systems and Computers.Pacific Grove，2008:533-537.

[10]Haimovich A M，Peckham C，Ayoub T，et al.Performance analysis of reduced-rank STAP[C]//Processing of the 1997 IEEE national Radar Conference， Syracuse， New York，1997:42-47.

[11]Zatman M.Properties of Hung-Turner projections and their relations to the eigencanceler[C]//1996 Conference Record of the Thirtieth Asilomar Conference on Signals，System and Computers， Pacific Grove， CA USA，1996:1176-1180。