電力系統(tǒng)穩(wěn)定器對低頻振蕩抑制效果的研究

李昂

（陜西理工學院 電氣工程學院，陜西 漢中 723003）

電力系統(tǒng)運行時，在負荷突變等小擾動的作用下，發(fā)電機轉(zhuǎn)子之間會發(fā)生相對搖擺，這時電力系統(tǒng)如果缺乏必要的阻尼就會失去動態(tài)穩(wěn)定。由于電力系統(tǒng)的非線性特性，動態(tài)失穩(wěn)表現(xiàn)為發(fā)電機轉(zhuǎn)子之間的持續(xù)的振蕩，同時輸電線路上功率也發(fā)生相應的振蕩，影響了功率的正常輸送。由于這種持續(xù)振蕩的頻率很低，一般在0.2～2.5 Hz之間，故稱為低頻振蕩。低頻振蕩在國內(nèi)外均有發(fā)生，通常出現(xiàn)在遠距離、重負荷的輸電線路上，或者互聯(lián)系統(tǒng)的弱聯(lián)絡(luò)線上，在采用快速響應高放大倍數(shù)勵磁系統(tǒng)的條件下更容易出現(xiàn)。

目前，電力系統(tǒng)普遍采用在勵磁調(diào)節(jié)器上附加電力系統(tǒng)穩(wěn)定器（PSS）的附加勵磁控制方案。它能有效地增強發(fā)電機勵磁系統(tǒng)的阻尼，抑制低頻振蕩的發(fā)生，是提高電力系統(tǒng)動態(tài)穩(wěn)定性的最經(jīng)濟和最有效的的措施。PSS在國內(nèi)外得到了廣泛應用，我國新投運的大中型發(fā)電機組都要求安裝PSS[1]。本文介紹了低頻振蕩的產(chǎn)生機理及發(fā)電機附加勵磁控制對低頻振蕩的抑制原理，通過對一個典型的單機—無窮大系統(tǒng)在不同擾動方式下的動態(tài)過程仿真，說明了附加勵磁控制對電力系統(tǒng)動態(tài)穩(wěn)定性的影響。

1 低頻振蕩產(chǎn)生機理

一般認為，發(fā)生低頻振蕩的主要原因是現(xiàn)代電力系統(tǒng)中大容量發(fā)電機的標幺值電抗增大，造成了電氣距離的增大，再加之遠距離重負荷輸電，造成系統(tǒng)對于機械模式（其頻率由等值發(fā)電機的機械慣性決定）的阻尼減少了；同時由于高放大倍數(shù)的快速勵磁系統(tǒng)提供的附加勵磁電流在相位上滯后于轉(zhuǎn)子角的變化，進一步加重了負阻尼的狀況，即對振蕩的阻尼起了相反的作用，也就是所謂的“負阻尼”作用。

大型同步發(fā)電機勵磁系統(tǒng)一般由勵磁功率單元和勵磁控制部分（勵磁調(diào)節(jié)器）兩部分組成。由于勵磁調(diào)節(jié)器按照發(fā)電機端電壓偏差進行調(diào)節(jié)，也稱為自動電壓調(diào)節(jié)器（AVR），它是勵磁主控制器。隨著自動化技術(shù)的發(fā)展，調(diào)節(jié)器的調(diào)壓精度越來越高，勵磁電源的響應也越來越快。快速勵磁系統(tǒng)的確能夠改善同步轉(zhuǎn)矩，從而提高系統(tǒng)在第一搖擺周期的暫態(tài)穩(wěn)定性。然而，快速勵磁系統(tǒng)一般是高放大倍數(shù)的負反饋系統(tǒng)，它對第一搖擺周期以后系統(tǒng)振蕩的阻尼影響很小，有時甚至減小系統(tǒng)對振蕩的阻尼。在系統(tǒng)呈現(xiàn)負阻尼特性時，快速勵磁系統(tǒng)（特別是高放大倍數(shù)時）通常是增大負阻尼，從而惡化系統(tǒng)的運行情況[2]。

并不是所有勵磁裝置都產(chǎn)生負阻尼，理論和實踐都證明，在遠距離重負荷輸電的單機—無窮大系統(tǒng)完整的線性模型（又稱Phillips-Heffron模型，如圖1所示）中，由于可能變負值，并且由于高放大倍數(shù)快速響應勵磁系統(tǒng)的存在，可能導致系統(tǒng)中的阻尼為負，一旦此負阻尼比發(fā)電機阻尼繞組、勵磁繞組的正阻尼和機械正阻尼還強，則系統(tǒng)在頻率擾動下可能出現(xiàn)振蕩失穩(wěn)。這時如果實際存在的發(fā)電機電氣的和機械的正阻尼較小，則該系統(tǒng)可能發(fā)生低頻振蕩[3]。

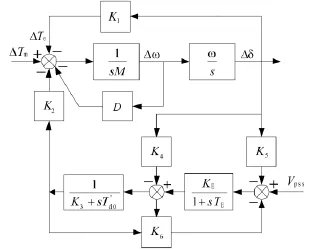
圖1 單機-無窮大系統(tǒng)Phillips-Heffron模型Fig.1 Phillips-Heffron model of single machine-infinite bus system

式中：xe、vc分別為發(fā)電機與系統(tǒng)間的聯(lián)系電抗、系統(tǒng)母線電壓；其余為發(fā)電機參數(shù)和運行變量。

2 電力系統(tǒng)穩(wěn)定器的工作原理

重負荷、高放大倍數(shù)的快速勵磁系統(tǒng)是引起低頻振蕩的主要原因。因此，當出現(xiàn)低頻振蕩，可以通過減少輸送容量，增強網(wǎng)架結(jié)構(gòu)（使K5>0），或者退出快速勵磁系統(tǒng)，改用手動或常規(guī)勵磁調(diào)節(jié)器來處理。但前者不經(jīng)濟，后者不利于大擾動下的暫態(tài)穩(wěn)定，因此最根本的方法是設(shè)法引入一個附加的阻尼力矩，這可以通過設(shè)置電力系統(tǒng)穩(wěn)定器PSS來解決。

PSS是一種附加勵磁控制，其實質(zhì)是提供勵磁系統(tǒng)一個附加信號，通過勵磁系統(tǒng)去增加發(fā)電機的阻尼轉(zhuǎn)矩。它可以使用發(fā)電機轉(zhuǎn)子速度、加速功率或系統(tǒng)頻率，以及這些信號的組合作為輸入信號。PSS具有物理概念清晰、現(xiàn)場調(diào)試方便、現(xiàn)場工作人員易于接受掌握等優(yōu)點。

圖2給出PSS傳遞函數(shù)框圖。PSS裝置包括信號處理單元、隔直單元、超前—滯后單元、放大單元和限幅單元。系統(tǒng)中的振蕩信號通過PSS時經(jīng)信號處理單元濾波后接入隔直單元；隔直單元濾掉小于等于0.01 Hz的直流次要信號，該單元只有輸入的頻率大于0.01 Hz時才輸出信號，否則自動閉合，處于待命狀態(tài)；超前—滯后單元補償傳感器、高頻濾波器及其它單元對主要信號所造成的相位滯后，該單元根據(jù)需要可以有不同的級數(shù)；放大單元將補償后的信號放大；限幅單元的作用是防止故障時發(fā)電機的機端過電壓。

圖2 PSS通用框圖Fig.2 Ordinary block diagram of PSS

圖中：K 為增益，Tw為隔直環(huán)節(jié)的時間常數(shù)，T1、T2、T3、T4為超前—滯后環(huán)節(jié)的時間常數(shù)。

若取Δω為PSS輸入信號，其傳遞函數(shù)為GPSS（s）=GPSS＜ΦPSS。PSS輸出VPSS作為勵磁附加控制信號，由圖1可知附加的阻尼力矩為

若使 GPSS（s）的超前相位 ΦPSS恰好等于式（2）分母的相位Φ3，則

以Δω為輸入信號的PSS使用的是超前網(wǎng)絡(luò)，超前網(wǎng)絡(luò)在高頻段增益變大，所以對發(fā)電機扭動振蕩極為敏感，使扭動振蕩更加嚴重。以ΔP作為輸入信號，檢測方便，所需超前角度小，穩(wěn)定性好，已得到廣泛應用，但存在反調(diào)現(xiàn)象。以ΔP和Δω同時為輸入信號，它們可以相互補償，減小反調(diào)現(xiàn)象的影響[4]。本文就以ΔP和Δω同時作為輸入信號的PSS（如圖3所示，圖中Kp為功率增益、KΔ為頻率增益）加以探討。

圖3 輸入信號為ΔP+Δω的PSS框圖Fig.3 Block diagram of PSS in ΔP+Δω input

圖4 PID勵磁控制傳遞函數(shù)框圖Fig.4 Transfer function of PID excitation control

3 附加勵磁控制對抑制低頻振蕩的仿真

3.1 勵磁控制系統(tǒng)模型

為了保證問題研究具有普遍性，本文選擇了典型的單機一無窮大電力系統(tǒng)，如圖5所示。該系統(tǒng)由發(fā)電機組、變壓器、雙回輸電線路、廠用電負荷和無窮大系統(tǒng)組成。其中發(fā)電機系統(tǒng)由同步發(fā)電機、勵磁控制系統(tǒng)（AVR+PSS）構(gòu)成；無窮大系統(tǒng)由12 000 MVA電源和500 MVA負荷復合而成。同時依據(jù)問題研究的側(cè)重點，忽略原動機的出力變化，供給同步發(fā)電機恒定的機械功率。選擇Step（階躍）函數(shù)作為信號源；PID環(huán)節(jié)、限幅環(huán)節(jié)、PSS環(huán)節(jié)為封裝子系統(tǒng)。仿真參數(shù)設(shè)置：Start time為 0，Stop time為 30；Solver options為 Variable-step和 ode23tb（stiff/TR-BDF2）；Relative tolerance 為 1e-3，其他參數(shù)為默認參數(shù)。

圖5 單機-無窮大系統(tǒng)模型Fig.5 Single machine-infinite bus system

3.2 暫態(tài)過程仿真

搭建好圖5所示的仿真模型后，并將故障功能模塊參數(shù)設(shè)置后，對系統(tǒng)在大擾動和小擾動下的穩(wěn)定運行能力進行模擬仿真。

3.2.1 小擾動仿真

在t=14 s時，發(fā)電機機端電壓參考值階躍5%，進行小擾動仿真。如圖6所示的仿真波形來看，勵磁控制器表現(xiàn)出了很好的靜態(tài)穩(wěn)定性能，功角和轉(zhuǎn)速的擾動波動幅度很小，功角4 s后趨于穩(wěn)定，功角8 s后趨于穩(wěn)定。

3.2.2 大擾動仿真

在t=15 s時，升壓變壓器出線端三相短路，0.1 s后故障切除，進行大擾動仿真。

如圖7所示的仿真波形來看，功角在短路故障（大擾動）時迅速減小，故障消除后，由于勵磁控制器的調(diào)節(jié)作用迅速恢復穩(wěn)定運行（8 s后），轉(zhuǎn)子間的轉(zhuǎn)速也很快趨于同步（15 s后），功率振蕩較快平息，低頻振蕩得到有效抑制。

3.3 仿真結(jié)果分析

圖6 機端電壓參考值階躍時的仿真波形Fig.6 Simulation waves when adding disturbance of 5%

圖7 三相短路故障時的仿真波形Fig.7 Simulation waves when fault of three-phase short circuit

由上可見PSS有明顯的提高阻尼的作用。無論小干擾還是大干擾，都可以使負阻尼（或弱阻尼）變?yōu)閺娮枘幔矣泻芎玫倪m應性（魯棒性），可以滿足在各種運行方式下穩(wěn)定運行的需要。PSS的作用使得發(fā)電機產(chǎn)生了附加電磁功率，該附加功率增強了系統(tǒng)的阻尼，使第一次功角振蕩回擺的幅度明顯減小，明顯改善了發(fā)電機的運行特性。

4 結(jié)束語

電力系統(tǒng)穩(wěn)定器PSS對于電力系統(tǒng)穩(wěn)定性的作用程度主要取決于 2點：1）PSS的安裝位置；2）PSS的參數(shù)[7]。 文中采用以和同時為輸入信號的PSS作為勵磁附加控制系統(tǒng)，通過對單機—無窮大系統(tǒng)在大擾動和小擾動下的穩(wěn)定運行能力進行模擬仿真，定性的分析了勵磁控制系統(tǒng)對于穩(wěn)定性的影響。從仿真結(jié)果可以看出，PSS可以提供足夠的正阻尼，有效克服AVR的負阻尼作用，提高了系統(tǒng)動態(tài)穩(wěn)定性。但是在復雜多機系統(tǒng)中，型號及配置地點的選擇是相當復雜且重要的。若選擇不當，甚至會使系統(tǒng)低頻振蕩更為嚴重[8]。

[1]張茂盛.大型發(fā)電機勵磁系統(tǒng)淺析[J].山西電力，2007（6）：51-54.

ZHANG Mao-sheng.Analysis of large-scale unit of excitation system[J].Shanxi Electric Power，2007（6）：51-54

[2]王錫凡，方萬良，杜正春.現(xiàn)代電力系統(tǒng)分析[M].北京：科學出版社，2003.

[3]姚強.電力系統(tǒng)低頻振蕩及其抑制方式的研究與仿真[J].電工電氣，2010（12）：1-6.

QIANG Yao.Studyand simulation oflow frequency oscillation for power system and its inhibition method[J].Diangong Dianqi，2010（12）：1-6.

[4]楚文斌，劉覺民，劉軍志，等.具有新型PSS的勵磁系統(tǒng)建模與仿真[J].電機與控制應用，2009（12）:6-25.

CHU Wen-bin，LIU Jue-min，LIU Jun-zhi，et al.Modeling and simulation about included new PSS of excitation system[J].Electric Machines&Control Application，2009（12）:6-9.

[5]李維波.MATLAB在電氣工程中的應用[M].北京：中國電力出版社，2006.

[6]相偉，馬幼捷，周雪松，等.PID勵磁控制對比例式勵磁調(diào)節(jié)效果的改善[J].天津理工學院學報，2004（2）:5-7.

XIANG Wei，MA You-jie，ZHOU Xue-song，et al.The limitation of proportional control and the improvement of PID control of the excitation systems[J].Journal of Tianjin Institute of Technology，2004（2）:5-7.

[7]張帆，李劍峰，王偉，等.基于MATLAB的PSS和SVC對電力傳輸穩(wěn)定性的仿真[J].電氣開關(guān)，2009（1）:40-42.

ZHANG Fan，LI Jian-feng，WANG Wei，et al.The simulation of PSS and SVC to stability of electric power pransmission based on MATLAB[J].Electric Switchgear，2009（1）:40-42.

[8]倪以信，陳壽孫，張寶霖.動態(tài)電力系統(tǒng)的理論和分析[M].北京：清華大學出版社，2002.