無線傳感器網絡吞吐量的自適應跨層優化策略＊

丁凡，周永明

（韶關學院 物理與機電工程學院電子系，韶關 512005）

引 言

吞吐量是無線傳感器網絡（Wireless Sensor Network，WSN）的一項重要性能指標，它直接反映了無線傳感器網絡工作運行的效率[1]，如何提高吞吐量一直都是無線傳感器網絡研究的熱點。

R.J.Lavery在參考文獻[2]中首次建立了經典的Ad hoc網絡點對點鏈路模型，明確了點對點鏈路模型吞吐量的數學定義式。作者以吞吐量為優化目標，針對影響吞吐量的符號速率和數據包長度這兩個參數分別作了優化，得到了不同條件下的最優符號速率和數據包長。隨后Taesang Yoo等人在參考文獻[3]中提出了一種數學框架，采用符號速率、數據包長度、調制星座體積3個參數作為優化變量，實現了MQAM調制方式下點對點鏈路吞吐量的優化。其后的參考文獻[4－6]基于參考文獻[2]提出的模型和假設，對鏈路的吞吐量也作了類似的研究和優化分析。但是參考文獻[2－6]的吞吐量優化都是基于參考文獻[2]建立的Ad hoc網絡點對點鏈路模型，而目前針對無線傳感器網絡吞吐量的研究相對較少。

針對上述問題，本文將針對在WSN中如何最大化點對點鏈路吞吐量這一問題展開研究。為了最大化吞吐量，本文采用跨層優化機制，不僅考慮了符號速率和調制星座體積這兩個物理層（PHY）主要參數，還考慮了MAC層的數據包長度，通過PHY和MAC層參數的聯合優化，保證在不同通信距離下鏈路的吞吐量能夠達到最優。

1 系統模型和假設

為了簡化分析，本文只考慮WSN中兩個通信節點之間的點對點鏈路。WSN中點對點通信鏈路一般由單個的發射機、接收機以及無線通信信道組成[2]。假定發射機節點發送的每個數據包總長為K＋C＝L位，其中K為有用信息數據長度，C為循環冗余校驗碼CRC（Cyclical Redundancy Check），用來檢測每個數據包中的誤碼，在本文的仿真分析中C＝16位。接收機節點使用CRC校驗接收到的數據包。假定CRC只進行檢錯而沒有進行糾錯編碼，并且CRC有足夠的冗余度可以檢測到每個數據包的所有誤碼。當接收機接收到的數據包中不包含誤碼時，便發送一個ACK反饋幀給發射機，告之數據已經正確接收；否則發送一個NACK反饋幀。當發送節點接收到NACK幀時，便重傳該數據包，否則傳送下一個新的數據包。在實時通信中，ACK仍有可能產生誤碼，從而導致系統的吞吐量下降。為了簡單起見，這里假定ACK／NACK反饋幀在傳輸過程中不會出現誤碼。

根據參考文獻[2－3]，點對點鏈路的吞吐量可以定義為：每秒成功接收到的有用信息比特數。對于一個基于上述模型和假設條件的點對點傳輸鏈路，其吞吐量通式為：

其中，b為每個調制符號所包含的比特數，Rs為符號速率，f（b，rs，L）為包成功傳送率（PSR），它定義為正確地接收到一個數據幀的概率。PSR由下式給出：

這里，Pe為誤碼率，rs為符號信噪比，定義為：

其中Pr為信號接收功率，N0為AWGN信道中噪聲的半邊功率譜密度。

同時，接收信噪比定義為[2]：SNR＝Pr／（N0·B） （4）

其中B＝1MHz為系統帶寬。比較式（3）、（4），可以得到符號信噪比rs與接收信噪比SNR之間的關系為：

2 吞吐量分層優化

2.1 物理層參數優化

2.1.1 符號速率優化

為了找到最優符號速率R＊s，以使得鏈路的吞吐量達到極大值，對式（1）求關于Rs的偏導數并令該導數為0，即令?T／?Rs＝0，可以得到如下關于rs的微分方程：

可見要得到R＊s，應先求得最優符號信噪比r＊s。將式（2）代入式（6）中，可以由下式求得r＊s：

在AWGN信道條件下，采用MQAM調制時，誤碼率Pe近似為[1]：

一旦r＊s確定，便可以由式（3）得到相應的最優符號速率R＊s：

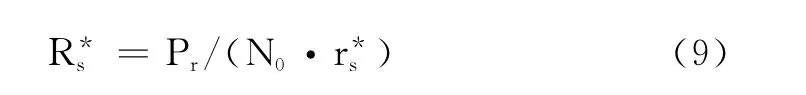
圖1給出了4種不同符號速率條件下，吞吐量與SNR的關系曲線。可以看出，當SNR較高時，鏈路能夠支持較高的符號速率，從而獲得較大的吞吐量；然而當SNR低于一定值時，吞吐量迅速減小，此時應采用較低符號速率以維持一定的吞吐量。因此，在實際的通信系統中，為了得到最優吞吐量，必須根據SNR進行自適應速率調整。根據式（8）可求解得到當L＝100、b＝2時，r＊s＝9.07dB。當SNR發生變化時，應根據式（9）來調節數據速率Rs，確保rs＝r＊s，以保證得到最優吞吐量。據此得到的最優吞吐量曲線如圖1所示。

圖1 不同符號速率Rs時的吞吐量（b＝2，L＝100位）

2.1.2 調制星座體積優化

從式（7）、（8）可以看到，調制星座體積b對Pe、rs也有影響，因而鏈路的最優吞吐量也取決于調制星座體積的大小。同樣，對式（1）求關于b的偏導數，并令?T／?b＝0，可得：

由上式可知，b＊取決于L、Pe和rs，而當rs＝r＊s時，b＊僅取決于L和Pe；根據不同調制方式下的誤符號率Pe，通過求解（10）式，可得該調制方式下的b＊。

圖2顯示了不同信噪比條件下，星座體積b對吞吐量的影響。由圖2可見，當信道條件較好，即SNR較大時，可以讓每個符號承載更多的信息位，即采用高階調制方式來提高系統的吞吐量；而當信道條件較差即SNR較小時，誤符號率較大，此時應該采用低階調制方式，以保證最優吞吐量。

圖2 不同星座體積b條件下的吞吐量（L＝100，Rs＝1MHz）

2.2 MAC層優化

在Rs及其他系統參數一定的條件下，可以找到一個使吞吐量最大的包長，稱為最優數據包長度，記做L＊。L＊可以用求極值的方法得到，對式（1）求關于L的偏導數，令?T／?T＝0，可求解得到最優數據包長度：

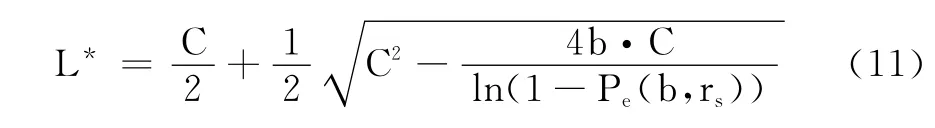
圖3比較了在不同SNR、不同包長L條件下鏈路吞吐量。如圖3所示，當SNR較大時，包長越大，吞吐量越大。這是因為，較近的通信距離使得信道條件比較好，信噪比較大，誤包率非常小，f（b，rs，L）≈1。此時吞吐量 T≈bRs（L－C）／L，即吞吐量與SNR無關，而是隨著L的增大而增大。但是吞吐量不會隨著L的增大而無限增大，當L＞＞C時，T≈b·Rs，即T的上限值為b·Rs。以上兩點結論均可從圖3中得到很好的驗證。但是L不宜過大，因為若L過大，可能會引入其他的問題，譬如延時等。因此，要權衡時延等因素而選取一個盡可能大的數據包長度L，在本文仿真中設定最大包長Lmax＝512[3]。

然而，從圖3中還可以看到，隨著SNR低于一定值時，吞吐量迅速下降為0。此時，求解式（11）得到不同通信距離下相應的最優數據包長L（d）＊，進而得到吞吐量的最優曲線，如圖3所示。從最優曲線可以看到，當SNR＜2dB時，T≈0，此時即使采用最優數據包長，提高不了吞吐量。因此，信道條件較差時，僅靠MAC優化并不能使吞吐量最大化。

圖3 不同數據包長L時的吞吐量（b＝2，Rs＝1MHz）

3 物理層和MAC層跨層聯合優化及自適應

在2.1～2.2節的分層優化中，只能求得吞吐量的極大值。為了使鏈路的吞吐量最大化，必須聯合物理層和MAC實現跨層優化，即在WSN中，根據接收信噪比SNR和分層優化中所推導出的最優等式，計算出最優配置參數（L＊，R＊s，b＊），然后自適應地在物理層調整Rs和b值，在MAC層調整L值。最優配置參數（L＊，R＊s，b＊）可聯立求解最優等式（7）、（10）、（11）而得到：

從而得到跨層優化后無線傳感器網絡點對點鏈路吞吐量的最大值：

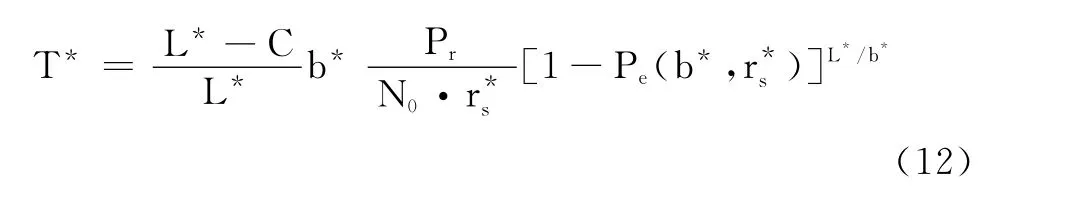
從圖1～圖3的分層優化仿真圖中可以看到：當SNR較大時，優化后的吞吐量的大小關系為T（b）＞T（L）＞T（Rs）；而當SNR低于一定值后，優化后的吞吐量的大小關系為T（Rs）＞T（b）＞T（L）。特別地，當SNR＜2dB時，T≈0，調節L或b均已經失去優化能力；而從圖1中可以看到，優化Rs后鏈路仍能獲得不錯的吞吐量性能。因此，為了使鏈路在不同的信噪比條件下都能有較高的吞吐量，必須進行跨層優化。

跨層優化后的最優吞吐量曲線如圖4所示，同時給出了兩種次優吞吐量曲線，以便進行對比分析。從圖中可以看到，兩條次優吞吐量曲線分別在較高信噪比（SNR＞2 dB）和較低信噪比（SNR＜2dB）條件下，與最優吞吐量曲線取得一致。因此，為了保證鏈路的最優吞吐量，可采取如下自適應調節策略：

① 高信噪比（SNR＞2dB）區：在此區域內信道條件相對較好，誤符號率很低，應盡可能采用高的符號速率；但由于受系統帶寬的限制，Rs≤B，所以單方面通過增大符號速率并不能使吞吐量達到最優。此時，可以通過讓每個符號承載更多的位信息，即采用高階調制方式以提高系統的吞吐量并聯合最優數據包長，可使吞吐量達到最優。最優參數對（b＊，L＊）可以通過聯立求解式（10）、（11）得到。

② 較低信噪比（SNR＜2dB）區：在此區域內信道條件急劇惡化，誤符號率Pe較大，此時應以盡量降低Pe為主。由式（8）知，MQAM調制的誤符號率主要取決于b和rs，為了盡可能降低Pe，應該采用BPSK，即b＝1；同時調節符號速率Rs以使rs＝r＊s。由式（11）可求解得到在此區域內應采用的最優數據包長L（d）＊＝L（b＝1，r＊s）。

通過上述自適應策略來配置相應的參數組（b，L，Rs），便可以保證在不同的信噪比條件下，鏈路的吞吐量始終能達到最優值。

圖4 跨層優化后的吞吐量對比

結 語

吞吐量是衡量無線傳感器網絡服務質量（QoS）好壞的重要標準。針對移動性無線傳感器網絡點對點鏈路的吞吐量問題，本文采用跨層優化分析的方法，定量地描述了兩個移動節點之間無線通信鏈路的吞吐量表達式。根據吞吐量表達式，選擇優化后的物理層參數符號速率Rs、調制星座體積b和MAC層參數數據包長度L，可以優化鏈路吞吐量。最后提出了一種能夠根據節點間通信距離自適應跨層調節的優化策略。根據該跨層優化策略自適應調節物理層和MAC層參數，保證了在不同通信距離下鏈路的吞吐量始終保持最大化。

在進一步的研究工作中，將建立多跳移動性無線傳感器網絡吞吐量模型，并研究該模型下的吞吐量優化問題。

[1] Goldsmith A.Wireless Communications[M].Cambridge：Cambridge University Press，2005.

[2] R J Lavery.Throughput optimization for wireless data transmission[D].New York：Polytechnic University，2001.

[3] Yoo T，Lavery R，Goldsmith A，et al.Throughput Optimization Using Adaptive Techniques（Draft），2005.

[4] Fakhri Y，Nsiri B，Aboutajdin D，et al.Throughput optimization via the packet length and transmission parameters[J].IJCSNS International Journal of Computer Science and Network Security，2006.

[5] Jian Liu，Jian Sun，Shoutao Lv，A Novel Throughput Optimization Approach in Wireless Systems[C]／／IEEE ICCT 2010，Nanjing，China，2010：1374－1378.

[6] Lin Dai，Khaled Ben Letaief.Throughput maximization of ad－hoc wireless networks using adaptive cooperative diversity and truncated ARQ[J].IEEE Transactions on Communications，2008，56（11）：1907－1918.

[7] J G Proakis.Digital Communications[M].4th Ed.New York：McGraw－Hill，2000.

[8] S Cui，A Goldsmith，A Bahai.Energy－constrained modulation optimization[J].IEEE Trans.on Wireless Communications，2005，4（5）：2349－2360.