考慮徑向加質的固體火箭發動機內流場整體穩定性分析①
楊尚榮,劉佩進,魏少娟,魏祥庚
(西北工業大學燃燒、熱結構與內流場重點實驗室,西安 710072)
0 引言
大型分段固體火箭發動機中的壓強振蕩主要是渦脫落現象引起的[1]。理論上,CFD(例如LES)可完整地模擬渦脫落與聲場的耦合過程,預示燃燒室內壓力振蕩的頻率和幅值[2]。但實際預估時,由于發動機幾何尺寸較大,工作時間又很長(大于100 s),對每一時刻的工作狀態進行數值模擬計算是不現實的,因此有必要從穩定性理論角度出發,對渦脫落的機理進行研究。
縮比發動機[3]和冷流實驗[4-5]都證明單純表面渦脫落也可引起發動機內的壓強振蕩,并且其振蕩幅值強于由障礙渦脫落導致的振蕩幅值[6]。與由剪切不穩定產生的障礙渦脫落相比,表面渦脫落被認為是由固體推進劑燃燒生成的徑向加質流的“本質不穩定”決定的[7]。相似的是,它們都可以用流動不穩定性理論來研究并獲得不穩定特征以及演化規律。
Casalis等[7]利用局部非平行方法討論了平面徑向加質流的不穩定模式,發現平均流的橫向分量對穩定性結果有很大的影響。計算結果表明分別用主變量和勢函數表示的擾動方程得到的結果會有差異[8-9],說明局部非平行方法是不一致的。文獻[10]同樣利用局部方法研究了圓柱構型的徑向加質流不穩定特征,但其與實驗結果的差距較大,認為該方法不太適合于圓柱構型的研究[11]。Chedevergne[11-13]采用了整體穩定性方法重新討論了該問題,解決了局部方法帶來的不一致問題,得到的特征值虛部即時間增長率皆為負值,即它們是時間穩定的。因此,其認為實驗中出現的表面不穩定現象應該是由某些外在的噪聲激發的。
本文使用更合理的邊界條件,利用整體流動穩定性方法研究了圓柱構型的徑向加質流整體不穩定特征,來解釋上述理論與實驗的差異,以加深對固體火箭發動機內由于表面渦脫落引起的不穩定現象的理解,并為分段發動機穩定性分析提供一種快速、有效的手段。
1 控制方程
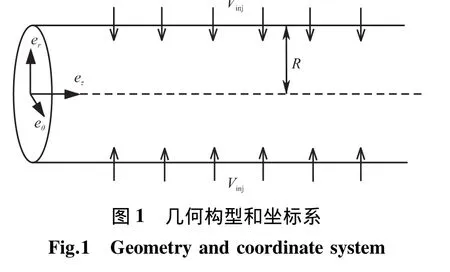
采用不可壓縮粘性流體N-S方程,在軸對稱坐標系下(圖 1),無量綱速度向量 U=(Ur,Uθ,Uz)和壓強 p滿足[11]:

其中,無量綱參考量為半徑R(長度)、徑向加質速度Vinj(速度分量)、R/Vinj(時間)、ρV2inj(壓強),密度 ρ假定為常數,雷諾數Re=VinjR/ν依賴于徑向加質速度和半徑,ν為運動粘性系數。
把瞬態解分解為穩態和擾動部分的和,U=Ub+u,p=pb+p,帶入方程(1),并消去 Ub,pb滿足的穩態方程,可以得到擾動方程:

流動穩定性分析便是在一定的邊界條件下去求解上述方程(2),得到擾動量u和p隨時間的變化(特征值)及其在空間的分布(特征函數)。方程(2)中用到了穩態流場解Ub,需要提前計算。在無粘且前端無滑移條件下,Taylor和Culick分別獨立地得到了方程(1)的穩態精確解[10],數值計算表明,在 Re>100時,精確解與數值解相當接近[7]。因此,本文采用該精確解進行穩定性計算,如下式所示:

2 整體穩定性分析
局部方法假定擾動量 q=(p,ur,uθ,uz)為如下形式:
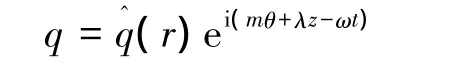
整體穩定性分析則把擾動量 q=(p,ur,uθ,uz)寫成如下的形式:

式中 m為整數,代表角波數;ω為復數,實部ωr代表無量綱角頻率,ωi代表時間增長率。
本文只討論軸對稱模態,此時m=0,uθ=0。把式(3)代入微分方程(2),便得到了如下的廣義特征值問題:

其中,A與B為3×3矩陣,各分量在柱坐標下的表達式為
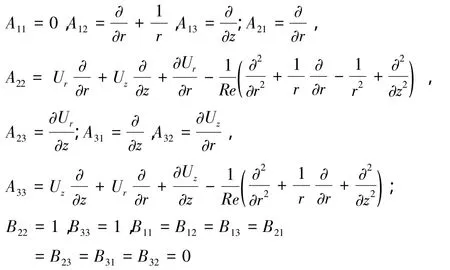
求解特征值(4)需要合適的邊界條件,速度擾動在頭部和壁面應為0,r=0處設為軸對稱條件。文獻[11]在嘗試了多種出口邊界條件之后,認為出口處取插值條件較為理想,但后來發現其結果與 DNS[14-15]結果相差較大。在研究后向臺階的瞬態增長時,Blackburn[16]認為出流邊界處取法向應力為0更為合理,本文出口處便采用了該種邊值條件。計算所用邊界條件總結如下:

3 結果分析
利用譜配置方法[17-18]和邊值條件(5)求解特征值問題(4),徑向×軸向網格量為20×50。數值計算了Re=2 100時的特征模態,如圖2所示。可看到長徑比L/R分別為10和8時,兩者特征值的實部,即無量綱角頻率ωr相差不大,但前者的虛部,即能量時間增長率ωi明顯大于后者,并且有些越過了臨界值0,由穩定模態變成了不穩定模態。這證明了文獻[15]中的猜測,即當長徑比大到一定程度后,ωi將為正值,時間特征由衰減變為增長。已有的冷流實驗[19-21]中長徑比都大于10,且都出現了表面不穩定現象,這與上述的理論結果一致,證明了外部噪聲不是產生表面不穩定的必要條件。

不同長徑比及特征值的擾動速度的分布見圖3。從圖3(a)看出,無論軸向擾動速度(上圖),還是徑向擾動速度(下圖),其沿軸向都是逐漸增大的,且向內部擴張。同一徑向位置,接近壁面的地方擾動達到最大,這與文獻[19]中實驗結果一致。徑向擾動速度在z=2的地方就已存在,其幅值比軸向擾動速度幅值小了一個數量級。圖3(b)為L/R=8時擾動速度的分布,該特征值與圖3(a)中的特征值有著相近的實部,但其虛部要小一些。兩圖中的擾動速度分布很相似,幅值也相差不大,只不過L/R=8時擾動存在的位置更靠前。與圖3(a)相比,圖3(c)不穩定波的波長較短,徑向擾動速度出現位置明顯靠后。

4 實驗驗證
為了與實驗結果比較,需把理論求解得到的一系列特征值ωM(其實部為角頻率),量綱化為

文獻[19]利用徑向加質軸對稱冷流實驗器對固體發動機燃燒室內的氣動聲學做了深入的研究。實驗器半徑 R=30 mm,空氣徑向加質速度 Vinj可在 0.8 ~2.0 m/s之間變化。在加質邊界附近測得的不穩定頻率隨徑向加質速度的變化如圖4所示,圖4(a)為徑向加質速度遞增時的擾動速度頻率,圖4(b)為徑向加質速度遞減時的擾動速度頻率。從圖4看到,理論和實驗吻合得很好。實驗中的不穩定頻率有數條軌跡,但它們都在理論解的范圍內。在徑向加質速度大于1.7 m/s時,實驗結果開始偏離理論值,應歸因于實驗中使用的供氣系統,壓力過高時,其與徑向加質速度的線性關系可能已不再適合。
Dunlap[20]設計的冷流實驗器半徑R=50 mm,氮氣徑向加質馬赫數見表1,實驗中氣體溫度在257~286 K之間,本文計算中選取了溫度的兩邊界值,取上界時,偏差在2%以內,取下界時,偏差在6%內。
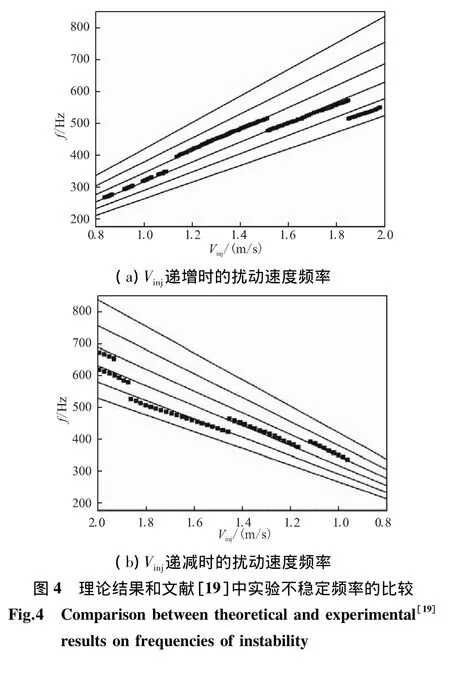
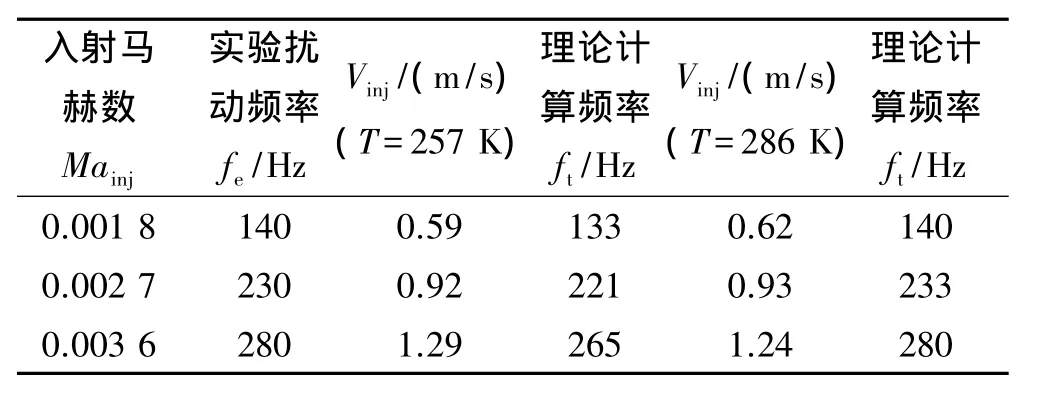
表1 理論結果和文獻[20]中實驗不穩定頻率的比較Table 1 Comparison between theoretical and experimental results[20] on frequencies of instability
VKI流體力學研究中心Anthoine[21]設計了Ariane 5 MPS的1/30縮比冷流實驗器來研究表面渦脫落引起的壓力振蕩。實驗器 L=0.63 m,D=0.076 m,噴管入口處馬赫數Ma0=0.09,按下式計算得到徑向加質速度[21]:
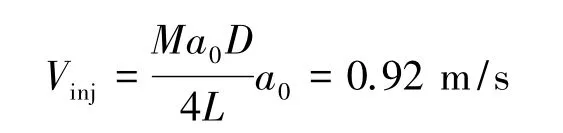
實驗中在L/R=10處測得的不穩定頻率為270 Hz和350 Hz,本文理論計算結果為273 Hz和337 Hz,偏差在4%以內。
5 結論
(1)圓柱形徑向加質流的整體不穩定分析發現特征譜是離散的,且隨著長徑比的增加,特征值的虛部明顯變大,而其實部變化不大,在L/R=10時虛部從時間穩定變為不穩定。
(2)特征函數表明,軸向和徑向擾動速度沿軸向逐漸增大,且向內部擴張,同一徑向位置,接近壁面的地方擾動達到最大。
(3)理論結果準確地估計了實驗中出現的不穩定頻率,證明流動穩定性方法可以解釋固體火箭發動機內的表面不穩定現象,也可以對發動機內的表面渦脫落現象和流動穩定性進行預估。
[1]Dotson K W,Koshigoe S,Pace K K.Vortex shedding in a large solid rocket motor without inhibitors at the segment interfaces[J].Journal of Propulsion and Power,1997,13(2).
[2]Zhang Q,Wei Z J,Su W X,et al,Theoretical modeling and numerical study for thrust oscillation characteristics in solid rocket motors[J].Journal of Propulsion and Power,2012,28(2).
[3]Lupoglazoff N,Vuillot F.Parietal vortex shedding as a cause of instability for long solid propellant motors:numerical simulations and comparisons with firing tests[R].AIAA 96-0761.
[4]Avalon G,Casalis G,Griffond J.Flow instabilities and acoustic resonance of channels with wall injection[R].AIAA 98-3218.
[5]Avalon G,Ugurtas B,Grisch F,et al,Numerical computations and visualization tests of the flow inside a cold gas simulation with characterization of a parietal vortex shedding[R].AIAA 2000-3387.
[6]Anthoine J,Lema M R.Passive control of pressure oscillations in solid rocket motors:cold-flow experiments[J].Journal of Propulsion and Power,2009,25(3).
[7]Casalis G,Avalon G,Pineau J P.Spatial instability of planar channel flow with fluid injection through porous walls[J].Physics of Fluids,1998,10(10).
[8]Griffond J,Casalis G.On the dependence on the formulation of some nonparallel stability approaches applied to the taylor flow[J].Physics of Fluids,2000,12(2).
[9]Griffond J,Casalis G.On the nonparallel stability of the injection induced two-dimensional taylor flow[J].Physics of Fluids,2001,13(6).
[10]Griffond J,Casalis G,Pineau J P.Spatial instability of flow in a semi-infinite cylinder with fluid injection through its porous walls[J].Eur.J.Mech.B-Fluids,2000,19.
[11]Chedevergne F,Casalis G,Feraille T.Biglobal linear stability analysis of the flow induced by wall injection[J].Physics of Fluids,2006,18.
[12]Chedevergne F,Casalis G.Thrust oscillations in reduced scale solid rocket motors,part Ⅱ:a new theoretical approach[R].AIAA 2005-4000.
[13]Chedevergne F,Casalis G.Detailed analysis of the thrust oscillations in reduced scale solid rocket motors[R].AIAA 2006-4424.
[14]Casalis G,Boyer G,Radenac E.Some recent advances in the instabilities occurring in long solid rocket motors[R].AIAA 2011-5642.
[15]Chedevergne F,Casalis G,Majdalani J.DNS investigation of the taylor-culick flow stability[R].AIAA 2007-5796.
[16]Blackburn H M,Barkley D,Sherwin S J.Convective instability and transient growth in flow over a backward-facing step[J].Journal of Fluid Mechanics,2008:603.
[17]Weideman J A C,Reddy S C.A matlab differentiation matrix suite[J].ACM Trans.Math.Softw.,2000,26(4).
[18]Trefethen L N.Spectral methods in matlab[J].Society for Industrial and Applied Mathematics,Philadelphia,2000.
[19]Cerqueira S,Avalon G,Feyel F.An experimental investigation of fluid-structure interaction inside solid propellant rocket motors[R].AIAA 2009-5427.
[20]Dunlap R,Blackner A,Waugh R,et al.Internal flow field studies in a simulated cylindrical port rocket chamber[J].Journal of Propulsion and Power,1990,6(6).
[21]Anthoine J.Experimental and numerical study of aeroacoustic phenomena in large solid propellant motors[D].PhD thesis,Universite libre,Bruxelles,October,2000.

