基于神經網絡的空白題識別技術及其在CET主觀題閱卷中的應用
肖 巍 辜向東
(南京師范大學,南京,210097;重慶大學,重慶,400044)
1.引言
隨著計算機技術的發展,一些大規模考試(如CET)的閱卷方式已由傳統的紙筆閱卷過渡到計算機甚至網上閱卷。其中,主觀題的閱卷一般是將原始試卷掃描成灰度圖像,再將圖像輸出到顯示器上供閱卷員評閱。以CET為例,先是將主觀題答題卡掃描成灰度圖像,再按題目將圖像分割成一個個小塊,每道題目為一個圖像文件,最后把一個個圖像文件依次輸出到顯示器。我們自身的CET 閱卷經歷以及對部分CET 閱卷員的訪談表明,每次CET 主觀題閱卷都會有一定數量的空白題。如果這些空白題不必由閱卷員評分,而是由計算機自動識別并賦分,無疑能減輕閱卷員的工作量,提高閱卷效率,降低閱卷成本,節約人力、物力和財力。
從掃描后的圖像來看,空白題和非空白題的主要區別在于像素灰度值,作答部分的灰度值接近0,空白部分接近255。但由于作答筆跡有輕有重,掃描清晰度不高,很難直接用像素灰度值加以區分(賈志先2009),需采用一定的技術進行識別。實現空白題自動識別的技術路線較多,如神經網絡、支持向量機等。其中神經網絡較為簡單實用。本研究將嘗試利用神經網絡進行空白題識別技術的開發,并討論該技術在CET主觀題閱卷中的應用。利用神經網絡進行空白題識別,最關鍵的是要保證識別的準確性與穩定性,即保證未作答的空白題一定賦0分,而考生作答了的一定不賦0分,留待人工評閱。如何確保空白題識別技術具有較高的準確性與穩定性是本研究需解決的主要問題。
2.理論基礎
神經網絡是一種能夠模擬人腦結構及功能的信息處理系統。其基本單位是神經元,這一點與人腦相似。神經網絡并不依賴事先編好的程序去運行,而是通過訓練去調整自身權值,具有自組織、自學習、非線性逼近的能力(Shiet al.2004)。由于神經網絡具有這些能力,它能夠反映人腦功能的許多基本特征,近年來在人工智能、自動控制、信息處理等方面取得了廣泛應用(董長虹2005;韓力群2006)。
在教育考試領域,神經網絡被應用于試卷等值、空白題識別等方面,如賈志先(2009)曾使用神經網絡識別HSK(漢語水平考試)的空白題,取得了較好的識別效果。通過學習空白題和非空白題的特征,不斷調整自身權值,神經網絡可以像人腦一樣把空白題準確識別出來。然而,HSK 用漢語答題,CET用英語答題,書寫文字的不同可能導致不同的識別效果。此外,若特征參數、實驗模型、訓練函數、學習函數、傳遞函數和隱藏層神經元數目等設置不同,識別效果可能也不同,需通過實證加以探究。我們的思路如下:首先提取可靠的特征參數,其次選取合適的網絡模型、函數及神經元數目,最后通過對網絡的訓練調試達到最佳識別效果。
2.1 空白題特征參數的提取
對空白題進行識別,首先要提取出能區分空白題和非空白題的特征參數。我們發現,空白題由于沒有任何作答記號,掃描后圖像各像素的灰度值均接近255,其標準差較小。非空白題由于有作答記號,掃描后這些作答部分的像素灰度值接近0,而其它部分的像素灰度值接近255,從而導致其標準差很大。因此,我們擬使用標準差作為區分空白題和非空白題的特征參數。
假設一幅圖像大小為m×n像素,則其像素灰度值矩陣為:

圖像像素灰度值矩陣A的行向量的標準差為:
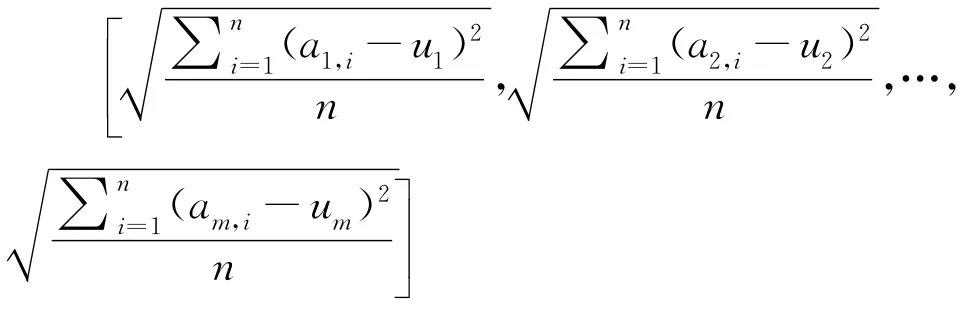
其中u1,u2,…,um為圖像灰度值矩陣A的各行向量的平均值。A的列向量的標準差為:
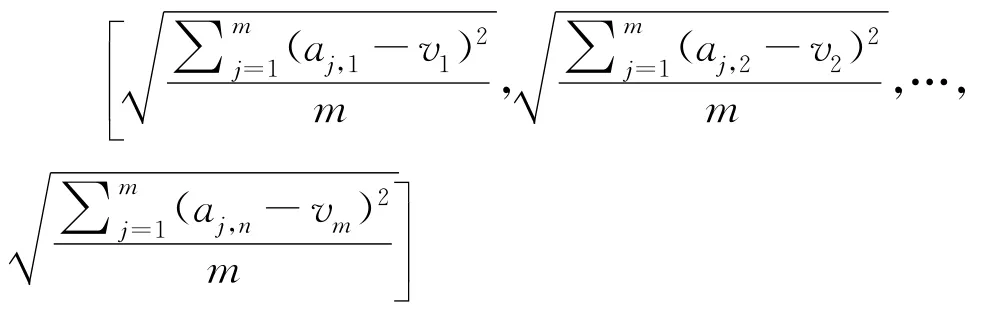
其中v1,v2,…,vn為圖像灰度值矩陣A的各行向量的平均值。
然而,直接以這些向量作為神經網絡的輸入,數據量太大,且由于m和n的取值不確定,神經網絡輸入層的神經元數目也無法確定。因此,我們對行向量和列向量的標準差繼續求標準差,得到一個二維數組[x1,x2],其中x1為行向量標準差的標準差,x2為列向量標準差的標準差。這樣,我們就可以用x1和x2兩個參數作為區分空白題和非空白題的特征參數。實現這些步驟的Matlab代碼為:
f=imread(‘...');∥載入圖像灰度值矩陣f,其中…為載入圖像的文件名∥
x1=std(std(double(f')));∥求行向量標準差的標準差,f'為圖像灰度值矩陣的轉置矩陣∥
x2=std(std(double(f)))。∥求列向量標準差的標準差∥
2.2 神經網絡模型的構建
使用神經網絡需根據研究自身特點選取合適的網絡模型。本研究選取Elman神經網絡模型。Elman網絡由Elman于1990年提出,并由Pham 和Liu于1992年加以改進,是一種動態的反饋網絡。該模型在前饋網絡的隱藏層中增加一個反饋層作為延時算子,以達到記憶的目的,從而使系統具有適應時變特性的能力,能直接反映動態過程系統的特性(Elman 1990;Pham&Liu 1992;Shiet al.2004)。其優點是對目標函數的逼近度高、自學習能力強;不足之處是需要的神經元數目可能較多,可能導致網絡結構龐大、學習時間較長。
Elman網絡由輸入層、隱藏層、反饋層和輸出層組成。輸入層用于輸入信號,隱藏層對來自輸入層的信號進行一定處理,反饋層用于記憶隱藏層前一時刻的輸出值并返回給輸入,即一步延時。輸出層的作用為對隱藏層傳來的信號進行加權輸出。這種特殊的網絡結構可以任意精度逼近任意函數(董長虹2005),具有較強的自學習能力,因此能夠較容易地學會對空白題的識別。結構圖可由圖1表示。
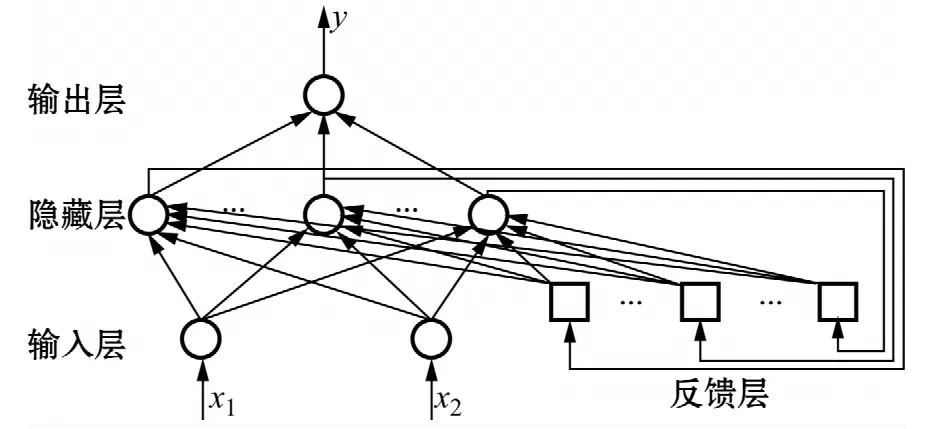
圖1 Elman神經網絡結構圖
該網絡的數學表達式如下:設網絡信號輸入為x(k),隱藏層輸出為x'(k),反饋層輸出為xc(k),信號輸出為y(k);W1、W2、W3分別為輸入層至隱藏層、反饋層至隱藏層、隱藏層至輸出層的連接權值;f(*)、h(*)分別為隱藏層和輸出層的傳遞函數;α(0≤α<1)為反饋層的自反饋增益因子,則該網絡的數學表達式為:
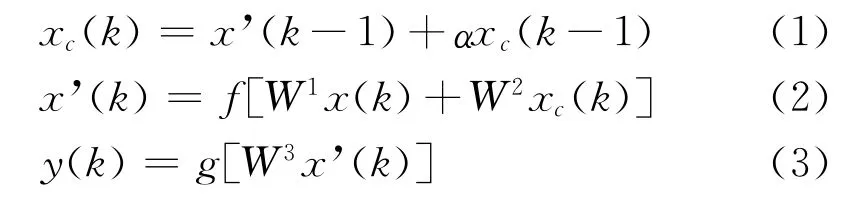
選定網絡模型后,還需選取網絡的訓練函數、學習函數、以及隱藏層和輸出層的傳遞函數。我們選取traindx函數作為訓練函數。該函數基于Levenberg-Marquardts優化算法,結合了梯度下降法和高斯—牛頓法的優點,其訓練速度較快且準確度高(王建梅、覃文忠2005;曹紅杏等2008)。以梯度下降動量函數learngdm 為學習函數。該函數利用神經元的輸入和誤差、權值或閾值的學習速率和動量常數來計算權值或閾值的變化率(董春嬌等2010)。分別以tansig函數、logsig函數作為隱藏層和輸出層的傳遞函數。tansig函數為S型正切函數,logsig函數為S型對數函數。在本研究中,輸入接近0(空白題)時需輸出0,輸入不接近0(非空白題)時需輸出1,輸入與輸出之間并非線性關系,故采用tangis和logsig兩類非線性函數比purelin等線性函數更滿足本研究的需要。
選定函數后,還需根據實際需要設定神經網絡各層的神經元數目。本研究中,輸入層神經元設為2個,分別接收行向量標準差的標準差x1以及列向量標準差的標準差x2。隱藏層的神經元數目過多會導致學習時間、可推廣性差,過少則難以保證學習精度和輸出的正確率(Suzuki&Mitsukura 2010)。一般情況下,隱藏層的神經元數目根據公式n'=(n+m)1/2+t來確定,其中n'為隱藏層神經元數目,n為輸入層神經元數目,m為輸出神經元數目,t∈{x$1<x<10,x∈N}(周開利和康耀紅2007;黨小超和郝占軍2010)。反饋層神經元數目與隱藏層相同。輸出層神經元設為1個,輸出對空白題的識別結果y,y接近0即為空白題,y接近1即為非空白題。
可見,為構建一個具有良好性能的神經網絡,需選擇合適的網絡模型、訓練函數、學習函數、傳遞函數,并設定合適的隱藏層神經元數目。網絡模型和各函數的選取依據各函數自身的特點及本研究的需要,隱藏層神經元數目的設定依據上述經驗公式。由上述經驗公式可知,本研究隱藏層的神經元數目取值范圍為3~11。我們使用訓練樣本對這些具有不同隱藏層神經元數目的神經網絡進行測試,評價其預測效果,從中選出最優模型。
3.實驗
我們使用Elman神經網絡進行處理的是二維的灰度圖像。如果掃描得到的原始圖像為有三個維度的RGB彩色圖像,需在進行實驗之前使用Photoshop等軟件將其轉換為灰度圖像。使用Photoshop的具體操作為:打開圖像,在菜單中依次打開“圖像”“模式”,選擇“灰度”,然后保存。一般設定圖像有256個色階,即灰度值區間為[0,255]。
圖2為實驗所用的一幅模擬CET 主觀題答題圖像,其內容為對2010年6月CET 六級考試一道主觀題的作答。該圖像為120×36像素的灰度圖像,每個像素的灰度值可在[0,255]區間內取值。
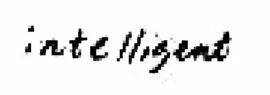
圖2 實驗圖像示例
3.1 Elman神經網絡的訓練
為加快網絡的收斂速度,我們對圖像的灰度值進行了歸一化,即將[0,255]區間的灰度值轉換到[0,1]區間內。
我們在Matlab中使用下列訓練樣本進行訓練:
輸入訓練樣本為:

目標輸出為:
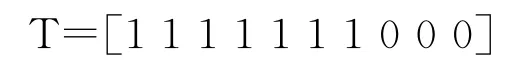
對網絡的設定為:

訓練結果見表1。
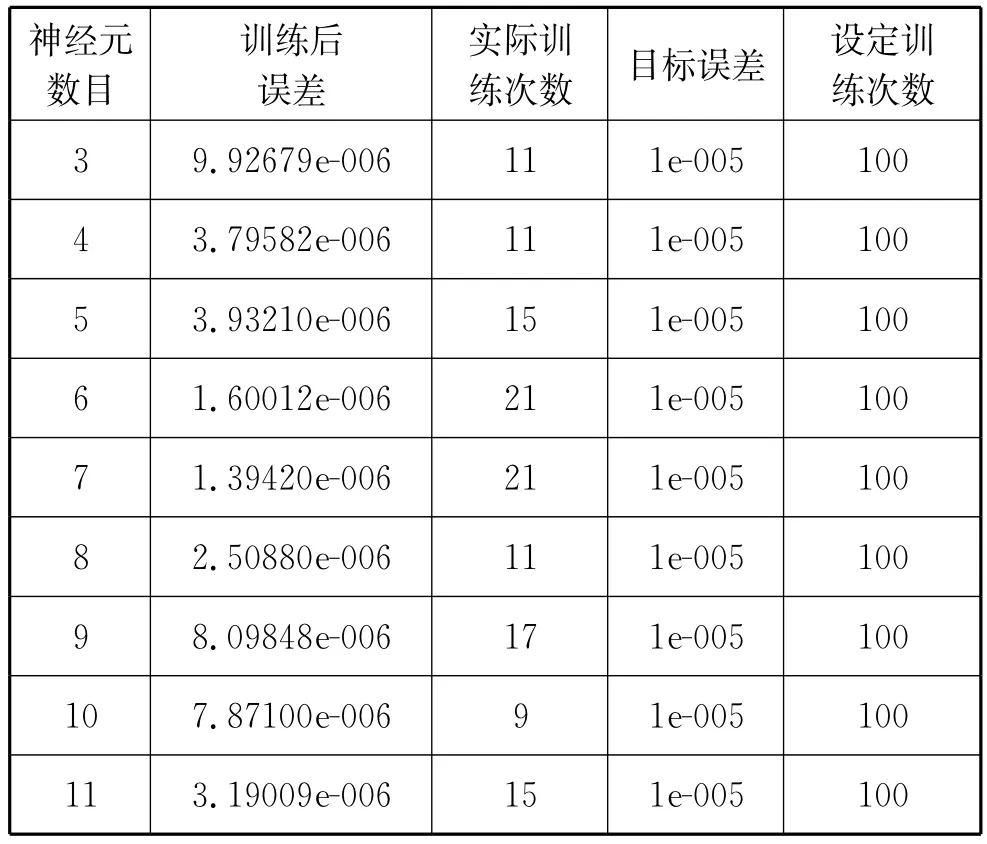
表1 隱藏層神經元數目的選取方案比較結果
由訓練結果可知,當神經元數目設定為7時,訓練后誤差最小,但訓練次數最多,為21次。神經元數目設定為10時訓練次數最少,但其訓練后誤差相對較大。經綜合考慮,我們選取神經元數目為8的方案,此時訓練后誤差為2.50880e-006,相對較小,且經過11次訓練就達到了設定的目標誤差,所需訓練次數也相對較少。這一數目與賈志先(2009)所做研究設定的7個神經元較為接近。
圖3為神經元數目為8時Elman網絡的訓練效果圖。
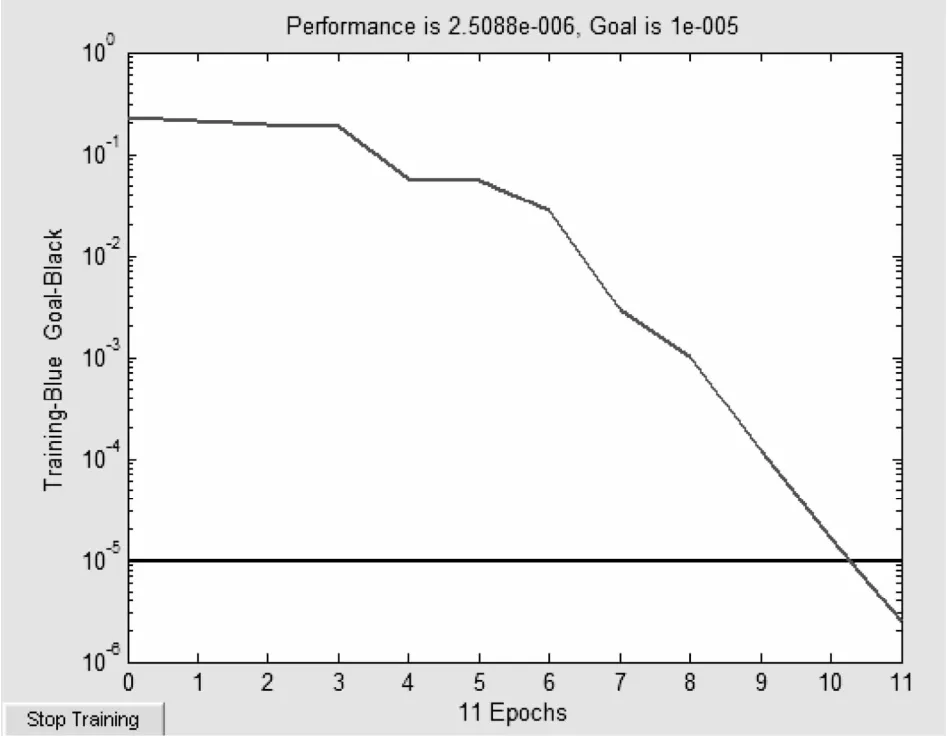
圖3 神經元數目為8時的Elman網絡訓練效果圖
由圖3可見,雖然訓練樣本較小(N=10),但經過11次訓練后,誤差達到了設定的最小值(10-5),表明該模型訓練成功,可以投入使用。
3.2 Elman神經網絡的測試
網絡訓練好以后就可用于空白題識別。我們使用以下數據進行測試。

網絡的輸出結果為:
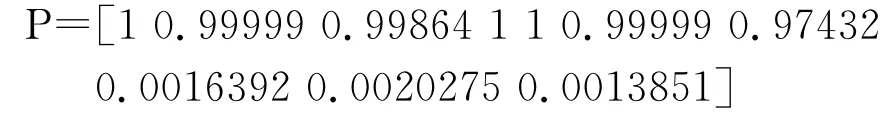
其中,前7個數據近似于1,表明輸入圖像為非空白題;后3個數據近似于0,表明輸入圖像為空白題。經過人工核對,識別結果完全正確。
測試結果表明,該Elman網絡可以較好地識別出空白題。
4.結論
本研究使用神經網絡進行空白題識別技術的開發,提取出圖像像素灰度值矩陣行向量、列向量標準差的標準差作為識別空白題的特征參數,選取Elman網絡模型為實驗網絡模型,以traindx函數為訓練函數,以learngdm 函數為學習函數,分別以tansig和logsig函數為隱藏層和輸出層的傳遞函數,通過對神經網絡隱藏層神經元數目的調整來優化網絡,使得網絡能夠以較少的運算消耗獲得較好的識別效果。初步實驗結果表明,該技術可以較好地識別出空白題。
本研究成功的關鍵是提取出區別空白題與非空白題的特征參數。因為非空白題有作答記號,導致其行向量、列向量標準差的標準差均較大,而空白題行向量、列向量標準差的標準差均接近0,所以我們提取圖像像素灰度值矩陣行向量、列向量標準差的標準差作為特征參數。為了更好地識別,可在提取特征參數之前對圖像進行增強對比度的預處理,以避兔對特征參數不明顯的試卷的“誤判”。此外,還可通過應用支持向量機的方法(如賈志先2011)進一步避兔可能出現的識別錯誤。
本研究只是利用神經網絡進行空白題識別技術開發的一個初步嘗試,尚存一些不足。首先,訓練樣本較小,識別的準確性和穩定性有待大樣本的驗證。其次,將彩色圖像轉換為灰度圖像的操作尚需人工處理,尚未實現“轉換-識別”的自動化。在后續開發中,如果實現了圖像轉換處理的自動化,且空白題識別的輸入結果能夠作為評分系統的輸入,自動給空白題賦分,那么這一基于神經網絡的空白題識別技術應當有廣泛的應用前景。

