材料性能和相對壁厚對管材助推彎曲影響的分析

樊子天，鄂大辛，陳吉生

(北京理工大學材料學院，北京 100081)

管材因具有質量輕，強韌性好，吸收沖擊性能好等優點，在航空航天、汽車制造領域中的應用越來越廣泛。由于在管材塑性彎曲中的彎管橫截面畸變和壁厚減薄規律一直沒能被很好掌握，因而阻礙了管材精確彎曲和數控彎曲技術的發展。根據管材力學性能和變形幾何條件，正確使用壓緊塊或尾部助推裝置可以有效減輕彎管橫截面畸變和壁厚減薄程度。由此，不同的材料性能和變形條件對管材助推彎曲的影響，已成為管材精確彎曲和數控彎曲技術領域中一個重要的研究課題。

文中在實驗的基礎上，借助于有限元方法，僅在壓緊塊助推條件下，研究了3種材料和不同相對壁厚管材的助推彎曲對橫截面畸變和壁厚減薄的影響，為管材彎曲生產提供參考。

1 實驗條件與有限元建模

1.1 實驗條件

實驗用管材為1Cr18Ni9Ti，TA0(工業純鈦)和5A03(防銹鋁)，管外徑 d0=20 mm，管壁厚 t0=2 mm，彎模半徑R=50 mm，彎曲角度θ=180°。彎曲實驗利用VB-200數控彎管機完成。實驗前對管材的幾何尺寸、平行度及圓度等進行測量并篩選。彎曲成形后，利用線切割方法切割試樣，測量并計算壁厚減薄率和短軸變化率。

為了分析管形狀態下材料力學性能對助推彎曲的影響，對部分管材進行直接拉伸試驗，供理論研究和有限元分析使用，測得真實應力應變σ-ε曲線如圖1所示。測算得出的材料力學性能參數見表1。

圖1 材拉伸狀態下真實應力應變曲線Fig.1 True stress-strain relation for different tubes

表1 不同管材的力學性能參數Table1 Mechanical property parameters for different tubes

1.2 有限元建模

為了提高有限元分析精度，直接加載時的硬化條件、變形條件、工藝參數的定義條件與得到真實σ-ε曲線的拉伸試驗條件完全相同。

圖2 管材彎曲有限元模型Fig.2 Finite element model of tube rotary draw bending

在DYNAFORM軟件中建立管材彎曲的三維有限元模型，如圖2所示。管材選用薄殼單元，厚度方向設7個積分點，彎模、夾緊模、彎模鑲塊、壓緊塊和防皺塊簡化為剛性單元。管坯與模具的接觸方式為面-面接觸，靜摩擦系數為 μs=0.15，動摩擦系數為μd=0.1。為防止相對滑動，夾緊模、彎模鑲塊和管坯之間采用零間隙配合，其余模具工作表面與管坯之間的單邊間隙為0.1 mm。有限元采用基于中心差分法的動態顯式時間積分算法和靜態隱式算法。并使用LS-DYNA非線性動力有限元求解器進行顯式成形仿真。

2 結果與討論

2.1 材料性能對管材助推彎曲成形缺陷的影響

2.1.1 彎管壁厚減薄

管材彎曲變形過程中，彎管內側壁的增厚直接影響輸送流體的流速和壓力的穩定性，外側壁厚減薄則降低承載能力，因此需要嚴格控制。在工程中，通常采用壁厚減薄率η表示彎管壁厚減薄程度:

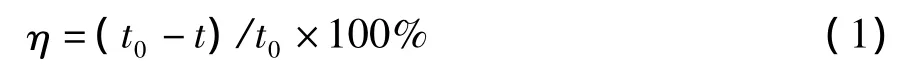
式中:t0，t——彎曲前、后管壁厚度，mm。

設管材彎曲前、后縱向線長度分別為l0和l，則彎曲切線方向和半徑方向的應變可分別表示為εθ=ln(l/l0)和 εr=ln(t/t0)。如果認為 εθ= －(εφ+εr)，在未產生橫截面畸變時，最內、最外側某一小區域中符合εφ=εr的軸對稱變形，因而有:

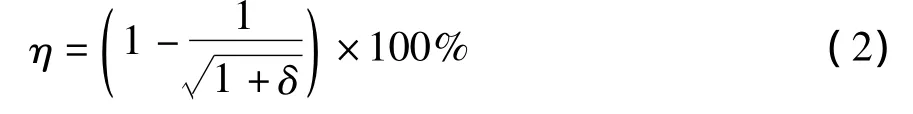
將按上述簡化公式計算的結果與3種管材有助推彎曲和無助推彎曲的壁厚減薄率分布如圖3所示，并與實測值進行比較，發現存在一定誤差，主要原因是沒有考慮材料力學性能參數及其切向彎曲變形方式的影響。

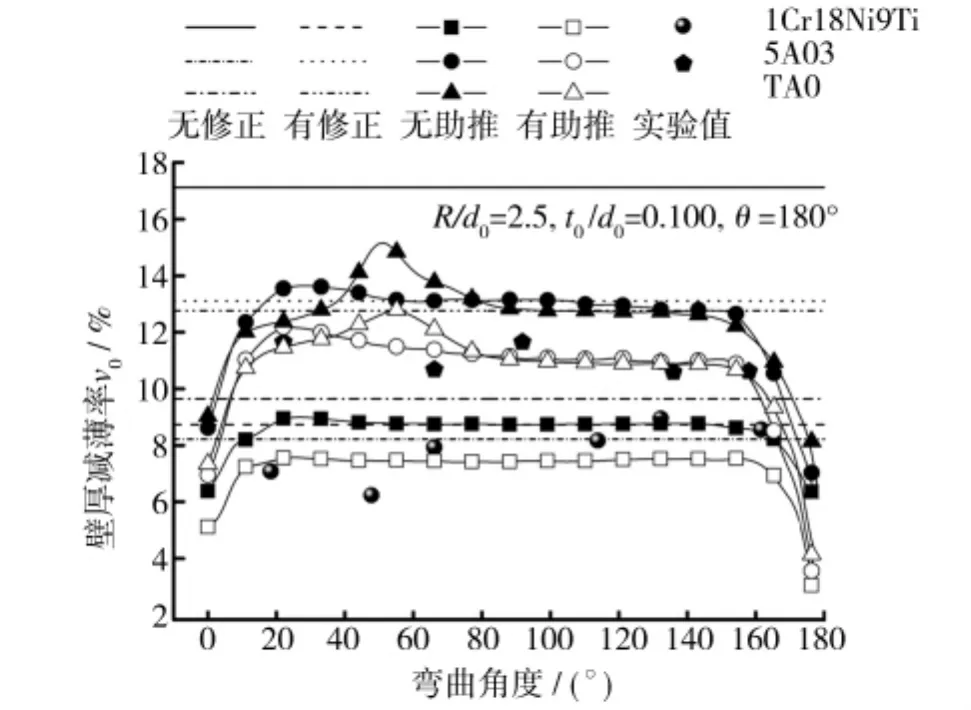
圖3 不同材料助推前后的壁厚減薄率Fig.3 Wall thinning ratio before and after boosting bending

由此，針對彎管外側變形特點，引入材料修正系數ξ，則管壁厚減薄率可表示為:

通過大量管材彎曲實驗驗證，確定了1Cr18Ni9Ti，5A03及TA0的材料修正系數ξ值分別為 0.510，1.595，1.322。與部分不同規格管材彎曲試驗進行比較，計算結果與測試值大致吻合。ξ的賦值原則主要根據表1所示的材料參數而定，由于計算式中沒能考慮其他材料性能參數和變形條件的影響，存在一定缺陷，需要修正。該公式可用于粗略估計彎管壁厚減薄率的大小，對管材彎曲生產具有一定的參考價值。

由圖3可知，助推彎曲使壁厚減薄率η有所減小，1Cr18Ni9Ti，5A03，TA0 管材助推前后最大壁厚減薄率 ηmax的絕對差值分別為 1.31%，1.36%，2.04%。由表 1 可知，1Cr18Ni9Ti，5A03，TA0 的屈強比 σs/σb分別為 0.28，0.38，0.56，硬化指數 n 分別為0.42，0.30，0.18，即1Cr18Ni9T 硬化最為嚴重，近似線性硬化，TA0硬化程度最弱，類似理想彈塑性材料。由此可見，屈服后TA0最易變形，5A03變形能力稍低于TA0，1Cr18Ni9Ti最難變形，故有|η|TA0＞ |η|5A03＞ |η|1Cr18Ni9Ti。單純從管壁厚減薄來看，壓緊塊同步助推有利于緩解彎管外凸側切向拉伸變形，但助推效果因材料性能不同略有差異。

2.1.2 彎管橫截面畸變

管材彎曲成形中，在彎曲切向拉應力作用下處于自由狀態的外凸側管壁材料具有向彎曲中心方向移動的趨勢，使彎曲半徑方向的管外徑減小，使彎管橫截面扁化變形。這將直接導致壓力流體輸送用彎管產生局部壓力損失和流量脈動。由此，通常將短軸變化率φs作為表征彎管橫截面畸變程度的重要缺陷指標。

式中:dmin為彎曲成形后管材橫截面內的最小直徑。

圖4所示為有限元模擬三種管材彎曲助推前、后短軸變化率差值 Δφ 分布(Δφ =φs－φa，φa為助推后的短軸變化率)。由圖4可見，助推彎曲使3種管材Δφ增大，即減小了橫截面扁化變形。Δφ的分布規律與φs相似，即始彎端的Δφ小于終彎端，這是由于整個彎曲過程中始彎端始終受到夾緊模的夾持約束作用，變形較小。此外，由于1Cr18Ni9Ti的伸長率δ和硬化指數n值較大，較好的延伸性和較強的變形抵抗能力使其Δφ均明顯大于其他2種材料，即相同的助推工藝對緩解1Cr18Ni9Ti彎管的橫截面畸變有更加明顯的作用。

圖4 助推前后短軸變化率差值有限元結果Fig.4 Finite element results of minor axis change rate difference

2.2 相對壁厚對管材助推彎曲成形缺陷的影響

工程中通常采用相對壁厚t0/d0來描述管材的幾何特征，t0/d0不僅表征管材自身的橫截面剛度，還可間接反映其對彎曲變形的抵抗能力。為了加深了解助推工藝對彎管成形缺陷的影響，需要研究不同t0/d0條件下管材常規彎曲和助推彎曲時壁厚減薄及橫截面畸變的變化情況。

2.2.1 彎管壁厚減薄

不同t0/d0的1Cr18Ni9Ti管彎曲時，助推前、助推后壁厚減薄變化率的有限元計算結果如圖5所示。由圖5可見，壁厚減薄率η隨t0/d0減小而增大。另外，其他變形條件相同時，助推工藝能有效地緩解彎管外側壁厚減薄程度，且助推前、助推后η的減幅也隨t0/d0減小而增大，即助推對減輕壁厚減薄的效果隨 t0/d0減小而愈明顯。當 t0/d0由0.167減小至0.083 時，相應的 η 最大減幅由1.30%增至2.96%。分析認為，在管壁厚t0一定的情況下，管徑d0越大，彎管的抗失穩能力及相對變形剛度越差，總變形量中的塑性成分越大，因此，t0/d0越小，η越大，變形敏感性也逐漸提高，從而使得助推效果更加顯著。

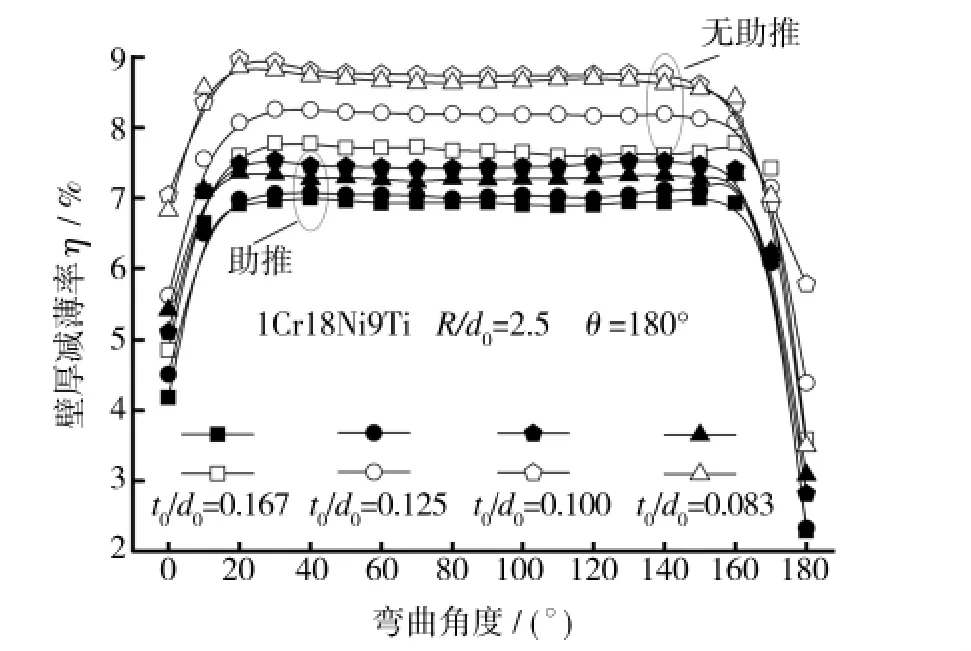
圖5 不同相對壁厚助推前后壁厚減薄率有限元結果Fig.5 Finite element results of wall thinning ratio for tubes with different relative wall thicknesses before and after boosting bending

2.2.2 彎管橫截面畸變

不同t0/d0下1Cr18Ni9Ti管材助推前、后短軸變化率差值Δφ的有限元計算曲線如圖6所示。與彎管外壁減薄變化趨勢類似，隨t0/d0不斷減小，Δφ逐漸增加，即截面畸變緩和程度越來越明顯。分析認為，彎曲變形程度一定的情況下，即相對彎曲半徑R/d0不變，減小t0/d0使得彎曲中性層附近的彈性區變形體積減小，增大總變形量中塑性變形成分，使彎管進一步發生變形而增大截面畸變程度。當t0/d0由0.166 減至0.084 時，Δφmax由1.81%增至3.43%，而Δφ增幅則逐漸減小。由此，對于部分大直徑管徑，助推工藝能夠有效地改善截面畸變程度，但隨管徑增大，其助推效果逐漸減弱。

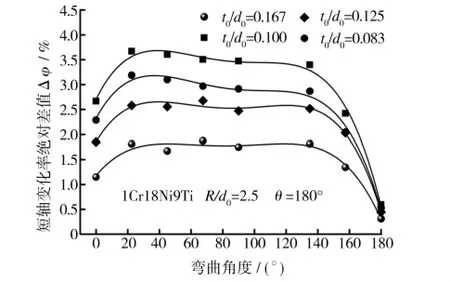
圖6 不同相對壁厚助推前后短軸變化率差值的有限元結果Fig.6 Finite element results of minor axis change rate difference for tubes with different relative wall thicknesses before and after boosting bending

3 結語

1)由于壁厚減薄率簡化公式僅考慮斷后伸長率而未考慮其它材料力學性能參數的綜合影響，使得計算值與實測值存在一定誤差。引入材料修正系數后，計算值與實測值吻合良好，可用于粗略估計彎管壁厚減薄率的大小。

2)對于不同材料的管材，壓緊塊同步助推有利于緩解橫截面畸變，減小彎管外凸側切向拉伸變形，但助推效果因材料性能不同而略有差異，相同的助推工藝對緩解1Cr18Ni9Ti管的截面畸變有更加明顯的作用。

3)不同相對壁厚t0/d0的管材，壓緊塊同步助推對壁厚減薄的影響效果隨t0/d0減小而明顯降低。對于大直徑管材，工程中采用助推工藝不能明顯改善壁厚減薄程度，但能夠有效地改善彎管截面畸變程度。

[1]MEGHARBEL A E，NASSER G A E，DOMIATY A E.Bending of Tube and Section Made of Strain-hardening Materials[J].Journal of Materials Processing Technology，2008，203:372 －380.

[2]MURATA M，KUBOKI T，TAKAHASHI K，et al.Effect of Hardening Exponent on Tube Bending[J].Journal of Materials Processing Technology，2008，201:189 －192.

[3]LI H，YANG H，ZHAN M，et al.Deformation Behaviors of Thin-walled Tube in Rotary Draw Bending under Push Assistant Loading Conditions[J].Journal of Materials Processing Technology，2010，210:143 －158.

[4]E Da-xin，CHEN Ji-sheng，DING Jie，et al.In-Plane Strain Solution of Stress and Defects of Tube Bending with Exponential Hardening Law[J].Mechanics Based Design and Structure，2012，40:257 －276.

[5]E Da-xin，GUAN Z P，CHEN J S.Influence of Additional Tensile Force on Springback of Tube under Rotary Draw Bending[J].Journal of Materials Engineering and Performance，2012，21(11):2316 －2322.

[6]陳吉生，鄂大辛，張敬文.材料模型對1Cr18Ni9Ti管材拉伸有限元仿真的影響[J].精密成形工程，2012，4(4)，10 －12，80.