計及熱輻射及翼翅效應的VLGC溫度場計算

李小靈，谷運飛

（江南造船（集團）有限責任公司，上海 201913）

0 引 言

VLGC（大型全冷式液化氣船），通過內置于貨艙區內的A型獨立菱形液貨艙來容納溫度為-50℃的貨物，盡管設有絕緣層，但受內外溫差引起的熱傳遞影響，貨艙區船體鋼結構工作溫度比較低。按照IGC（國際散裝運輸液化氣體船舶構造與設備規則）[1]要求，A型液艙的液化氣船必須考慮液貨艙破損的情況，故在VLGC的設計過程中需根據相關規定進行船體結構溫度場計算，并以此為依據選用合適等級的低溫鋼材。

1 規則要求及計算條件

在進行溫度場計算，并以此為依據選擇船體結構構件的鋼材等級時，除符合船級社一般要求外，還要滿足IGC和USCG（美國海岸警備隊）的特殊要求[2]。IGC和USCG規定的各個部分的邊界溫度假定和鋼材等級見圖1。

進行溫度場計算的環境條件須滿足以下要求，見表1。

表1 溫度場計算的環境條件

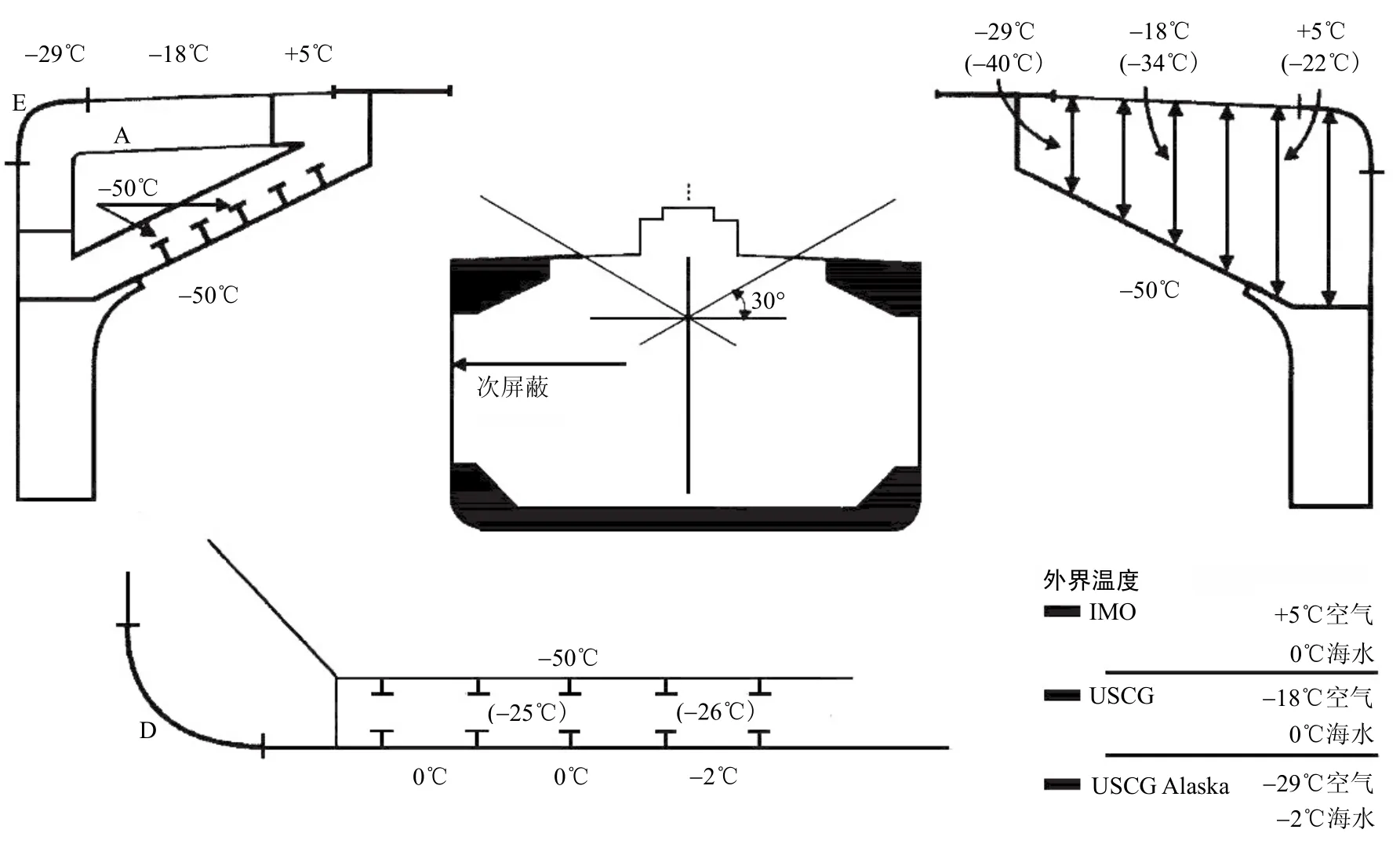
圖1 邊界溫度假定

進行計算時該船吃水狀態為結構吃水，正常航行工況下，此時的船舶與海水接觸面積最大，溫度場計算要求最為嚴格[3]。

對于液貨艙絕緣層，其物理特性為：

材料： 噴涂型聚亞胺酯

密度： 35～38kg/m3

20℃時熱傳導系數： 0.021W/(m·K)

厚度： 約120mm

外層保護： 聚合物表面保護層

除了液貨艙絕緣層之外，其他部位的熱傳導系數均需進行計算來獲得。

2 VLGC溫度計算分析原理

為了計算船體與液貨艙之間的溫度分布，需要進行熱傳遞分析。本項分析考慮對流和輻射兩種熱傳導模式，且設定對流傳導是沿著液貨艙絕緣材料厚度方向進行。

2.1 熱傳遞系數

船體結構的熱傳導機制主要取決于熱量的對流傳導和輻射傳導。對流傳熱模式是根據流體的自身特性可分為強制對流和自然對流。通常強制對流發生在流體受外力驅動而產生運動的情況；自然對流則是流體因自身溫度場分布不均導致密度不同而產生運動。因此，在船體內部的主要熱傳遞機制為自然對流，而在船體結構外部區域，為空氣和海水的運動，其熱傳導機制為強制對流。

2.1.1 自然對流傳熱

對流傳熱是指一個面和流體之間的熱傳遞過程。在自然對流傳熱中，流體的運動是由固（液）表面與流體之間溫度不同而產生的浮力所引起。自然對流傳熱通常由熱分布不穩定所引起。在較冷、較重的流體中溫暖、較輕的流體向上運動，流體中的不穩定流線越來越多，導致層流變為紊流。自然對流中邊界層的變化取決于流體的浮力和黏滯力的相對數量級。其發生通常與Rayleigh數有關。Rayleigh（Ra）數為Grashof（Gr）數與Prandtl（Pr）數的乘積，如式（1）所示。

Grashof數和Prandtl數由式（2）和（3）定義：

式中：g——重力加速度；β——流體處于膜溫度時的容積膨脹系數（K-1）；L——特征長度；ν——流體處于膜溫度時的動黏滯率，（m2/s）；α——流體處于膜溫度時的熱擴散率，（m2/s）；pC ——熱容量；μ——動態黏滯度。

則Rayleigh數表示為：

式中：sT——表面溫度，（K）；T∞——流體溫度，（K）。

大型全冷式液化氣船的對流傳熱必須用無量綱系數進行計算，這些無量綱數包括Nusseult數、Grashof數和Prandtl數，Nusseult數用于衡量表面發生的對流傳導，它是Rayleigh數的函數。對流傳熱系數與Nusseult（Nu）數之間的關系可以表示為：

式中： h——對流傳熱系數（W/m2·K）；k——流體處于膜溫度時的傳導率（kcal/mhK）。

對流傳熱系數可以通過對 Nusseult數的定義來獲得。在自然對流傳熱中，Nusseult數通過一個對Rayleigh數和Prandele數的函數來定義，如式(6)所示：

在各種不同情況下Nusseult數的經驗表達式如表2所示。

表2 Nusseult數經驗公式

計算自然對流系數時需要特征長度值，特征長度值根據對流產生的方向取為一塊板的高度或寬度，如表3所示。例如，對于一個豎直的平面，該值通常為板的尺寸，但在加筋的一面，它是扶強材的間距。對于一塊水平板未加筋的面，特征長度為面積除以周長。

表3 對流傳熱系數

LPG、空氣和海水的物理特性如表4所示：

表4 LPG、空氣、海水的特性

2.1.2 熱輻射

在船體內部空間，由于板架之間溫度差異引起的輻射傳熱與自然對流傳熱類似。通常情況下，熱傳導中的自然對流傳熱是波動的，但是輻射傳熱隨著板架之間溫度差加大而上升。為獲得船體結構溫度的定量結果，計算中需要考慮輻射傳熱的影響。在本項計算中，考慮了板架之間以及船體與外界空氣之間的輻射傳熱，用式(7)定義輻射傳熱的相當熱傳導系數：

式中：1T、2T——相對輻射面開氏溫度，K；0T——流體空間溫度，K；σ——Stefan-Boltzmann常數，5.669×10-8W/m2K4；tε——有效發射率；12aaF-——輻射面之間外形系數。

輻射外形系數12aaF-表示從離開a1表面到達a2表面的輻射能量比例。對于箱型封閉空間，可以簡化為兩個對應面，并可進一步簡化為無限長度的平行平面。

單個表面的有效發射率的典型數值可以假定為：1) 帶涂層的壓載艙表面：0.66；2) 鋁箔保護的液貨艙絕緣：0.20；3) 涂裝后的干艙：0.90。

對于兩個相對面之間的熱輻射傳遞，有效發射率可以根據式(8)計算：

總的熱傳遞系數為對流、輻射和傳導之和。在計算中，傳導是最小的一部分，可以用翼翅因子或者是穿入某個空間鋼質邊界的橫截面積或有義厚度來表示。對于浸沒在海水中的外板部分，由于大量熱量傳入海水，該值比較高，同時會隨著航速上升而增大。處于航行狀態時，對外底板和濕舷側，總的傳熱系數約為300W/m2K。當處于停靠港口狀態時，該值比較小，外底板約為80W/m2K，濕舷側約為160W/m2K。對于裝載于帶有絕緣層的獨立液貨艙中的貨物，總傳熱系數一般約為300W/m2K或更大，周圍的鋼結構將趨于與貨物溫度一致。

2.1.3 翼翅效應

在船體結構中，所有艙室的板均設置縱向和水平加強筋作為加強。這些扶強材會導致鋼質板架的熱流量上升，即翼翅效應，見圖2。加筋表面的熱傳遞用翼翅效率來表示，該無量綱常數平均值通常取為0.8。對流傳熱的熱傳遞系數可以用翼翅效應進行修正：

式中： hfs——考慮翼翅效應修正后的對流傳熱系數； hc——初始對流傳熱系數； Af——加強筋表面積；Ac——平板表面積；ηf——翼翅因子。

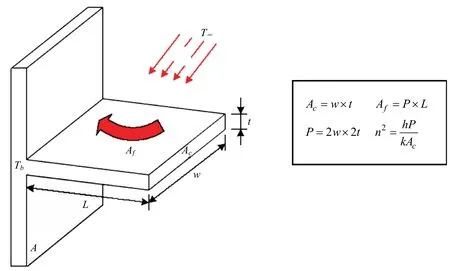
圖2 加筋表面的熱傳遞

2.2 熱平衡計算

在平衡狀態下，進入某個空間的總熱量和釋放的總熱量應該是相等的，以維持其熱平衡的穩定狀態，見圖3。在計算各個板架的相當熱傳遞系數后，某個空間內的溫度可以通過熱平衡方程來表示：

式中：iA——第i塊板的面積；iT——第i個外部空間的溫度；0T——內部空間未知溫度；ih——相當熱傳遞系數。

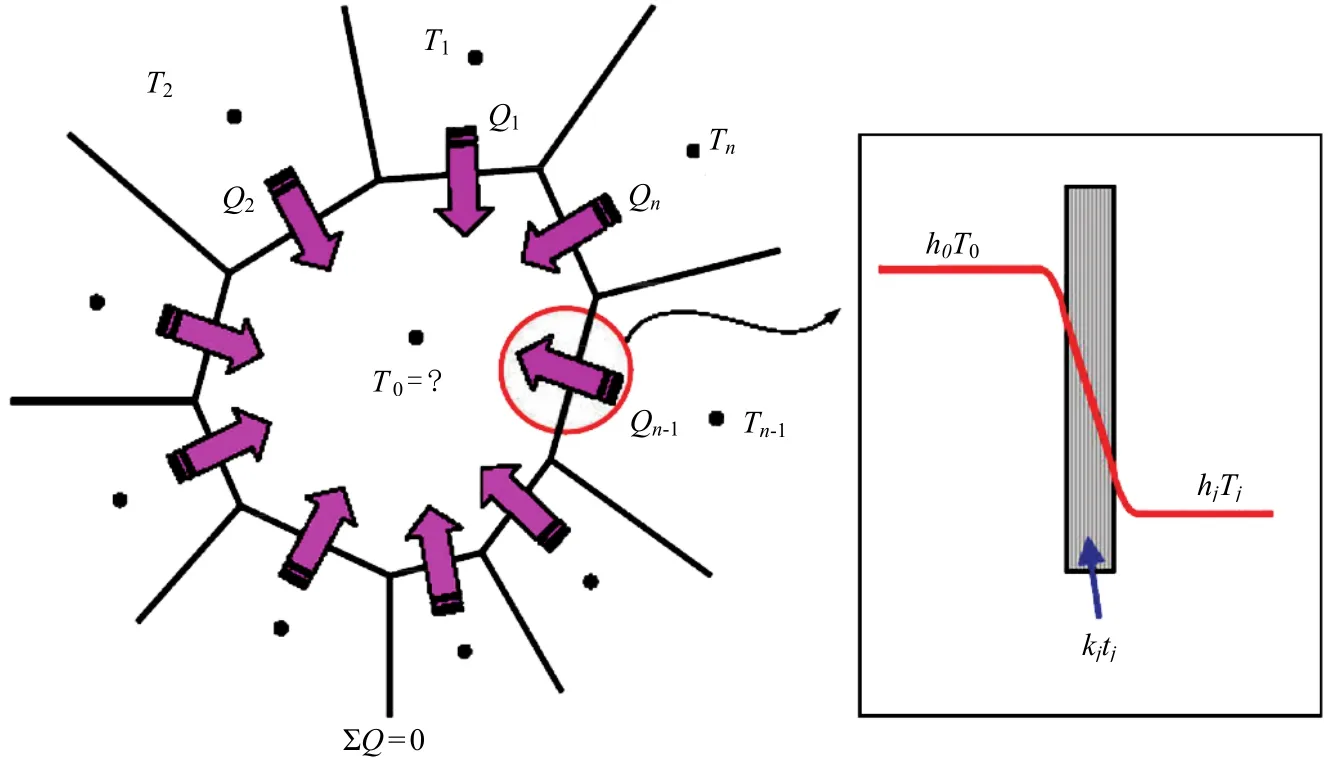
圖3 空間內的熱平衡

相當熱傳遞系數hi反映了多種熱傳遞模式，本計算中主要為對流和輻射。該系數可以表示為：

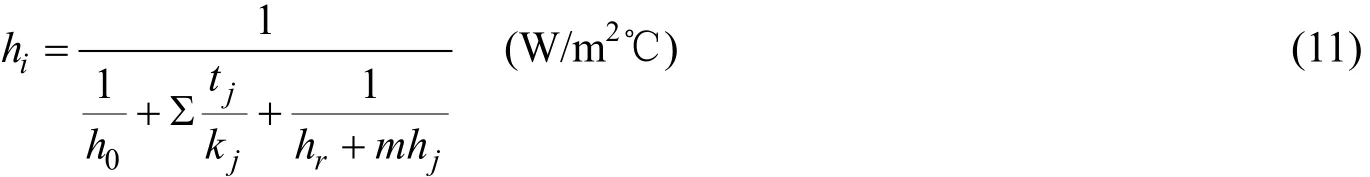
式中：jk——熱傳導率；0h——內邊界壁每邊的對流傳熱系數；jt——第j塊板的厚度；m——考慮加強筋的翼翅效應后的修正因子；rh——第j塊板的熱輻射引起的對流傳熱系數。

對于熱傳導率，通常選取值為： 鋼鐵：64.0（W/m·k）；絕緣層：0.021（W/m·k）。

為計及USCG以及USCG 阿拉斯加水域5節風速計算條件的影響，引入強制對流傳遞系數，見圖4，表示為7.2V0.78，其中V為風速，單位m/s，量綱為W/m·K，將其加入到自由對流傳遞系數，值為3.5W/m·K，范圍未暴露的甲板區域以及舷側部分未被靜水或波浪浸沒的區域。

對流傳熱系數h的計算主要受制于周圍物體、流體和溫度等影響熱傳導性能的因素，該計算花費時間較長，基于對精度的實際要求，對于外部大氣、內部空氣以及海水的對流傳熱系數的計算需先假定各體積溫度，通過數次迭代計算，直至計算值的偏差達到一定計算精度，則計算結束。

2.3 鋼板溫度計算

通過計算所得的空間內部溫度，可以計算出每塊鋼板的溫度，見圖5。

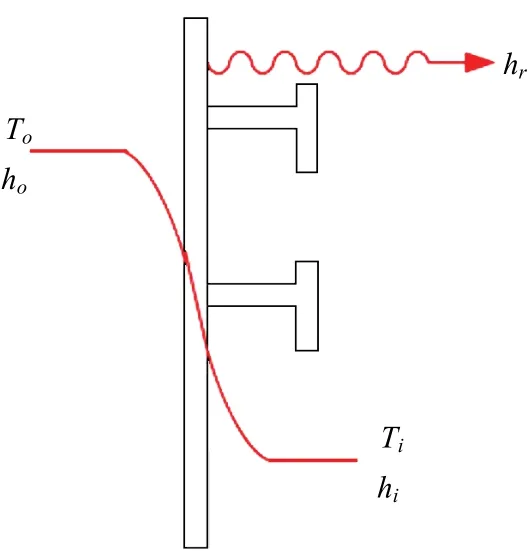
圖4 考慮翼翅效應和輻射的對流傳熱系數

圖5 雙層板和單層板的溫度分布

假如兩張不同材料的板疊在一起，兩邊的溫度1T、2T和3T可以計算出來。在平衡狀態下穿過各對流邊界的熱量是相等的。可以得到式(12)：

以矩陣形式表達，即為：

求解該矩陣方程，即可確定板架表面溫度。對于單層板來說，三次矩陣方程可以簡化為二次矩陣方程，如式(14)所示：

3 溫度場計算過程及結果

整個溫度分布計算流程如圖6所示。

圖7為簡化的計算模型，將模型分成21塊體積，其中7塊體積溫度為已知（為貨物溫度、外界空氣和海水溫度），14塊體積溫度未知，即有14個方程。

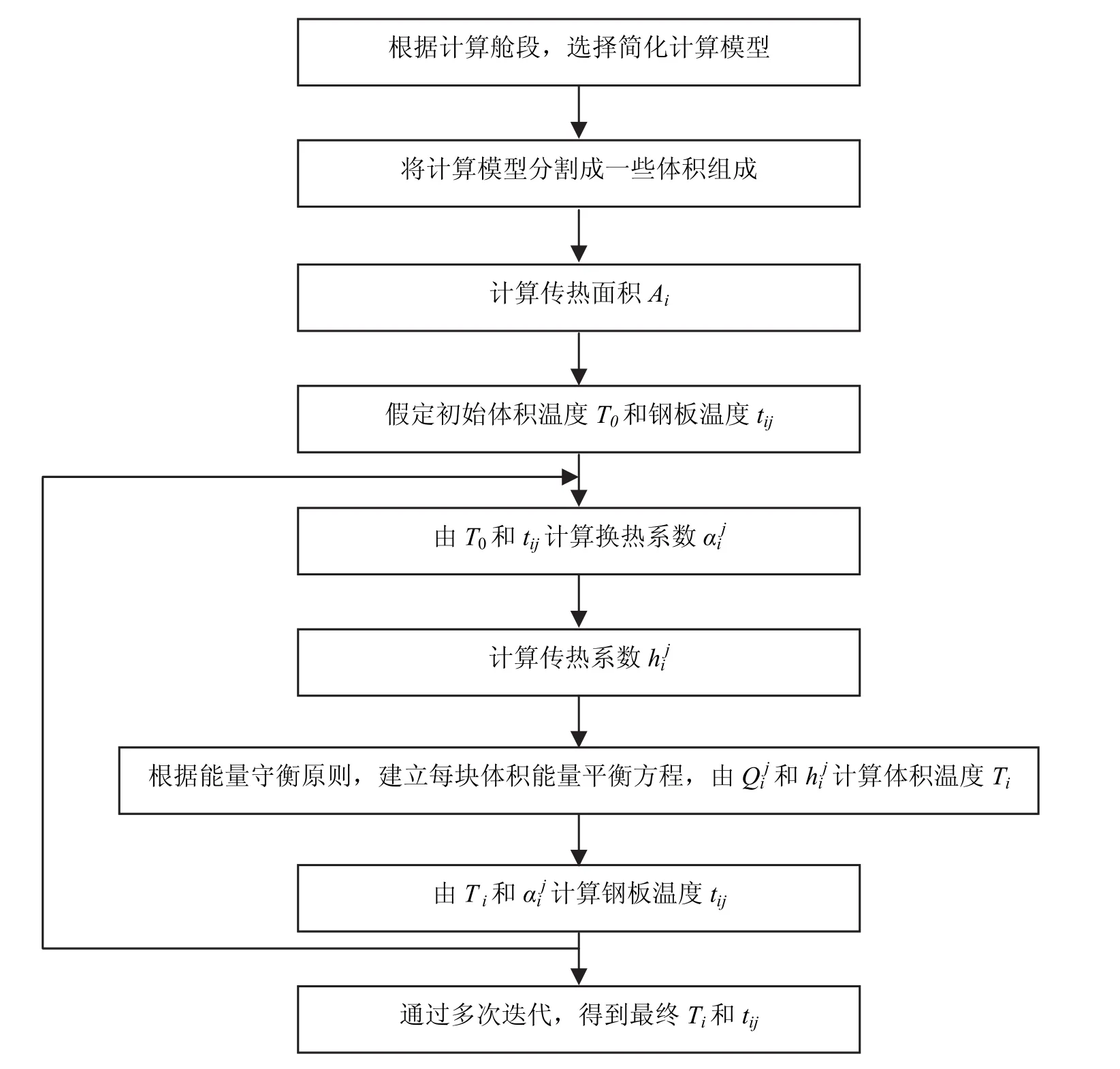
圖6 計算流程

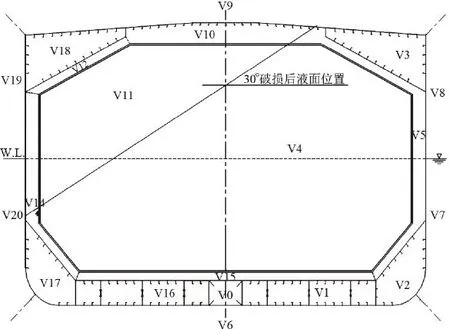
圖7 計算模型

21塊體積能量平衡表示為：

根據IMO及USCG的要求分別進行計算，實際計算表明，吃水對于水線附近的船體結構溫度影響較大，特別是根據USCG要求進行的計算。綜合IMO、USCG、USCG ALASKA的平浮和橫傾各種情況下的計算結果，得出貨艙區各構件溫度如圖8所示。

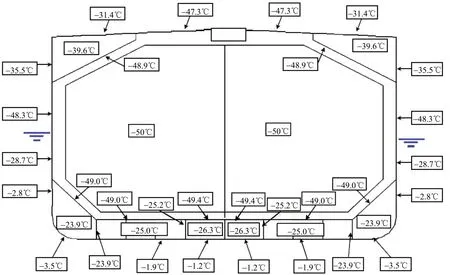
圖8 船體結構溫度計算結果

4 結 語

VLGC為高附加值船，目前其設計和建造均被日本和韓國壟斷[4]。對VLGC的溫度場計算進行研究，為船體結構鋼材等級的選用[5]提供了依據，為新型VLGC的開發和設計打下了良好的基礎。

[1] 國際海事組織（IMO）. 國際散裝運輸液化氣體船舶構造與設備規則[S]. 1993.

[2] 美國海岸警衛隊（USCG）. Electronic Code of Federal Regulations (e-CFR)，Title 46： Shipping，PART 154—Safety Standards for Self-propelled Vesseds Carrying Bulk Liquefied Gases[S]. 2004.

[3] 英國勞氏船級社（Lloyd’s Register）. Rules and Regulations for the Construction and Classification of Ships for the Carriage of Liquefied Gased in Bulk[S]. 2010.

[4] 胡可一. 數字化技術在造船業中的應用[J]. 上海造船，2011, (1)： 31-33.

[5] 顧 俊，王凡超. 液化氣運輸船溫度場分布研究及鋼材匹配[J]. 船舶與海洋工程，2012, (4)： 1-5.