一種新的網絡傳播中最有影響力的節點發現方法*

胡慶成 尹龑燊 馬鵬斐 高旸 張勇 邢春曉

(清華大學計算機系,信息技術研究院,清華信息科學與技術國家實驗室,北京 100084)

(2013年1月25日收到;2013年3月25日收到修改稿)

1 引言

現實世界中的諸多系統都以復雜網絡形式存在,比如互聯網、社會系統、計算網絡、生物網絡和社交網絡等.理解復雜網絡的拓撲結構和功能是目前國際研究的熱點.在很多科學領域中,都使用網中絡用來節表點示代系表統人中,邊成代員表之人間與的人關之系間,如的在聯社系交.由網絡于這些網絡具有很高的復雜性,因此被稱為“復雜網絡(complex network)”[1-3],它已成為當前最重要的多學科交叉研究領域之一.在復雜網絡中,找出最具影響力的節點[4-9]或意見領袖[10]在理論和現實應用中都有重大的意義,例如有效地控制疾病傳播[11]、流言散布[12,13]、計算機病毒擴散,還可以傳播新產品[14]、新思想[15]以推進社會化進程.

在社會網絡分析中,常用“中心性(centrality)”來測量最有影響力的節點.文獻[16,17]利用度中心性(degree centrality)來測量最有影響力的節點,在符合冪律的非均勻網絡中,度數較大的hub節點的傳播影響力應該相對較大,這也是目標免疫和熟人免疫策略的基本依據.文獻[18]利用了介數中心性(betweenness centrality)來評價影響力,介數中心性是以經過某個節點的最短路徑的數目來刻畫節點的重要性.文獻[19]提出PageRank算法來評價網頁的重要性,它認為一個網頁(節點)的重要性取決于其前向鏈接的數量與質量.文獻[20,21]利用緊密度指標(closeness centrality)刻畫某個節點到其他節點的難易程度.文獻[22]提出通過K-shell(ks)[23]分解來確定最具有影響力的單源節點.

本文認為節點的影響力不只是由節點內部屬性決定,而且其外部屬性緊密相關,這與哲學范疇的內因和外因思想一致.內部屬性如度數、緊密性、介數等中心化指標,外部屬性如所屬社區的大小、社區內關系緊密度等.社區[24,25]是一個有共同愛好的,或者位于一個共同地方的、或者同在某個工作場所的、或者具有家庭聯系的群體[26].社區內的節點聯系緊密,社區間的節點聯系松散.

本文提出了KSC(K-shell and community centrality)指標模型.此模型不但考慮了節點的內部屬性,而且還綜合考慮了節點的外部屬性,例如節點所屬的社區特性等.然后利用SIR(susceptible-infected-recovered)模型對傳播過程進行仿真,實驗證明本文提出的方法可以更好地發現最具有影響力的節點.本文為這項具有挑戰性研究提供了新的思想和方法.

2 相關研究

在社會網絡中,發現最具有影響力的節點可以幫助我們有效地控制疾病傳播、流言散布、計算機病毒擴散,還可以傳播新產品、新思想以推進社會化進程.

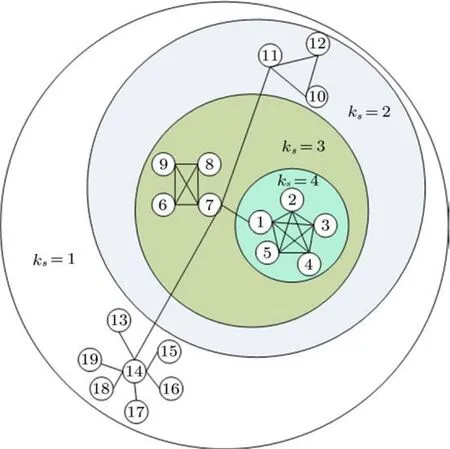
圖1 網絡分析樣例圖

2.1 度中心化

度中心化[27,28]是一種最簡單的方法,用于描述在靜態網絡中節點所產生的直接影響力.設網絡G=(V,E)具有n=|V|個節點和m=|E|條邊,節點v的度數是指與節點v連接的節點個數,用Cd(v)表示

其中d(v)稱為該節點的度.如圖1所示,盡管節點14度數最大為7,但作為初始節點,它最終的傳播范圍并不一定是最廣泛的,因為它的鄰居節點的度數都很小.

2.2 介數中心化

介數中心化刻畫了網絡中節點對于信息流動的影響力.節點v的介數[18]定義為

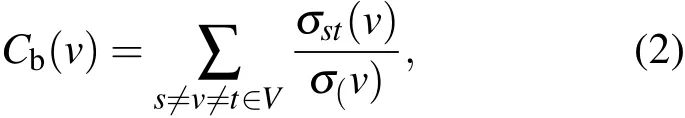
σst表示源節點s到目標節點t的最短路徑數,σst(v)表示節點s經過節點v到目標節點t的最短路徑數.

2.3 緊密度

緊密度[20,21]用于刻畫節點到達其他節點的難易程度：

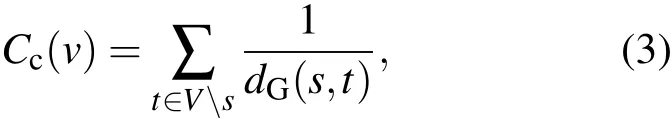
dG(s,t)表示源節點s到節點t的最短距離.

2.4 K-shell分解方法

K-shell給出了網絡中節點重要性的一種粗粒化的劃分,用Cks(v)表示.網絡邊緣節點的K-shell為1,然后往內像剝洋蔥一樣一層層進入網絡的核心.首先去除網絡中度數小于k的所有節點及其連邊;如果在剩下的節點中仍有度值小于k的節點,那么就繼續去除這些節點,直至網絡中剩下的節點的度值不小于k.依次取k=1,2,3,···,就得到了該網絡的K-shell分解.具體過程可參考圖一.Kitsak等[22]實驗研究表明,對于單個傳播源感染率低的情形,度數大或者高介數的節點不一定是最有影響力的節點,而通過K-shell分解分析確定的網絡核心節點(即K-shell值大的節點)才是最有影響力的節點;其研究表明,K-shell分解方法是一種比較好的影響力節點識別方法,可以更好地預測疾病等的傳播.當傳染病在網絡的K-shell大的節點爆發時,病毒總是可以在網絡核心通過許多種路徑開始感染其他部分,無論該節點度數的大與小,這個結論都是有效的.這些通路的存在反過來也意味著如果以一個隨機節點為源爆發疫情,有高K-shell值的節點更有可能早于其他節點被感染(疾病預測).

2.5 社區劃分算法

社區[24,25]是一個有共同愛好的、或者位于一個共同地方的、或者同在某個工作場所的、或者具有家庭聯系的群體[26].社區內的節點聯系緊密,社區間的節點聯系松散.社區劃分(community detecting)的概念前期在Lin的論文[29]中提出.如圖1,網絡劃分為4個社區(節點1—5,6—9,10—12,13—19).社區是復雜網絡信息傳播中最普遍和最重要的拓撲屬性之一,信息在同一社區內傳播迅速,而在社區之間傳播緩慢.Kernighan-Lin(KL)算法[30]、快速Newman(FN)算法[31]和Guimera-Amaral(GA)算法[32]是經典的復雜網絡社區劃分算法.

本文使用了FN算法.FN算法是Newman提出的基于局部搜索的快速社區劃分算法.其優化目標是極大化網絡模塊性(modularity)評價函數Q[26].FN算法屬于聚合算法,它初始假定所有節點各自成為一個社區,然后每一步根據原有連接合并兩個社區,計算Q值并記錄下來,直到所有社區都被合并成為一個社區.最后根據記錄下的Q值,找到最優的劃分結果.

3 算法模型

我們認為節點的傳播力不但與節點的內部自身屬性有關,如度數、緊密度、介數、K-shell等,還與它的外部環境屬性相關,如節點所處外部環境：社區大小,社區關聯緊密度等.本文提出節點的影響力是由內因與外因同時決定的這一新穎思想和方法,即KSC中心化指標模型.模型符合哲學內因與外因對事物同樣具有決定作用這一思想理念.

復雜網絡G=(V,E)中,節點vo的KSC值定義如下：

其中 f internal(vo)為節點的內部影響力,f external(vo)為節點的外部影響力,α為內部影響因子,β為外部影響因子,且滿足α+β=1,α和β可以根據實際網絡結構與功能設定.

f internal(v o)定義如下：

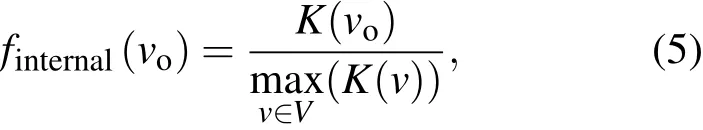
其中,K(v)為節點內部屬性值,可取度數、介數、緊密度和K-shell等節點自身屬性,mv∈aVx(K(v))為歸一化因子.

f external(v o)定義如下：

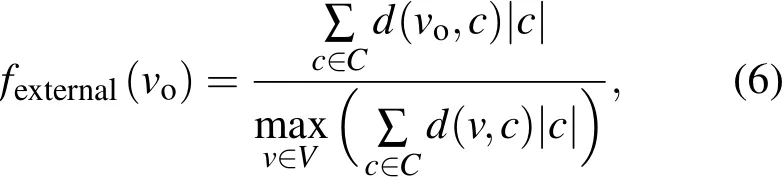
其中C為FN算法劃分的社區集合,d(vo,c)為節點vo在社區c中的鄰居節點的總個數,|c|為社區c的大小是歸一化因子.

本文實驗中α與β可以根據網絡的拓撲結構設定;其中 finternal(vo)選取K-shell為內部屬性,也可以為度數、緊密度和介數等,fexternal(vo)選取為社區屬性,俗語“物以類聚,人以群分”說明社區內部節點之間有共同的興趣愛好等,相似性更大.

表1給出了圖1各節點的各種指標,如節點14度數最大,但是由于處在網絡的邊緣,所以最終影響力為2,而節點7雖然度數為6,但是它是其他幾個社區連通的樞紐,結構洞[33,34]概念中重要節點.節點1—5雖然K-shell相同,但是節點1是2—5連接其他節點的橋接關系.從表1中可以看出各種方法得到的最具影響力節點排名各不相同.

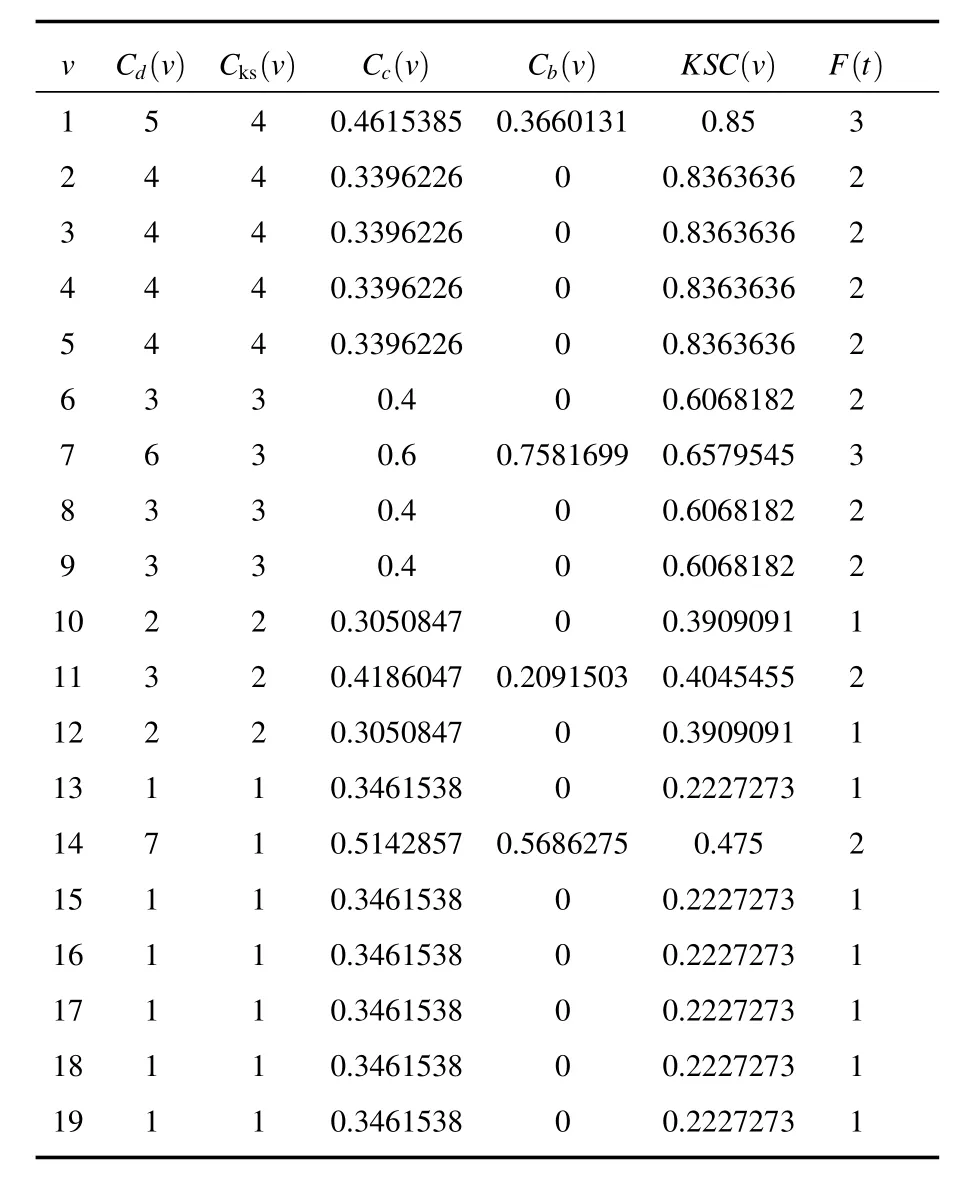
表1 計算圖一中節點的傳播力

4 模型及實驗分析

4.1 SIR模型

SIR模型在現實社會網絡中已廣泛應用于疾病傳播、信息傳播及謠言傳播的研究.為了驗證本文提出的模型,我們采用SIR模型[35-38]來模擬仿真傳播過程,并將其結果與我們的模型實驗結果做比較.

SIR模型中有三種狀態,易感染狀態S(susceptible),感染狀態I(infected),免疫狀態(recovered).當個體處于感染狀態時,以β的概率感染處于易感染狀態鄰居個體,感染狀態的節點以γ的概率恢復為免疫狀態.

如果β值較大,節點傳播能力很強,節點將很快感染整個網絡,從而很難區分單個個體的重要性;較小的β能在有限時間內更好地顯示出感染范圍.本文中我們設定較小的β=0.04.

4.2 實驗數據

考慮到不同的社會網絡類型所代表不同的網絡拓撲結構特性,我們選取了4個真實社會網絡數據集[39]進行分析比較,表2給出各個網絡的屬性特征：1)Blogs網絡數據[40],MSN博客空間中交流的關系網絡;2)Netscience合著關系網絡[41],選擇了其中最大連通子圖379個作者的關系網絡;3)Router網絡,數據是由Rocketfuel Project[42]收集的互聯網中路由連接層級關系網絡;4)Email網絡[43],是洛維拉·依維爾基里大學成員郵件通信的關系網絡.我們的模型也可應用于其他類型的復雜網絡.

其中n是節點數,m為邊數,〈k〉表示網絡中平均度數據,max(k)為節點中最大度數,d為節點之間最短路徑的平均數,max(Cks)為網絡中最大的K-shell,C為整個復雜網絡被劃分的社區數.

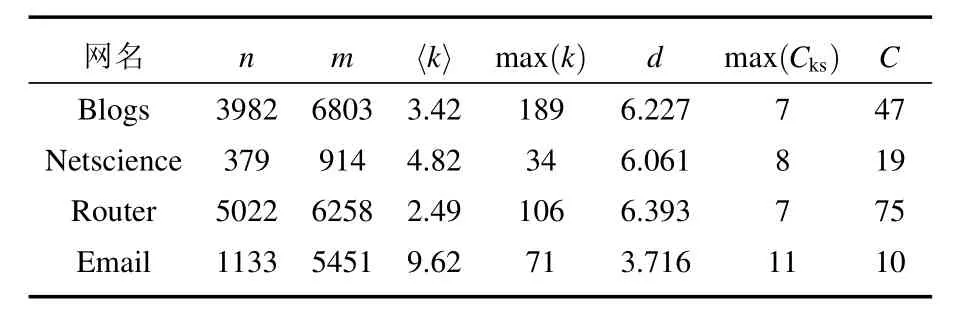
表2 現實社會網絡的屬性情況

4.3 實驗效果

我們應用章節4.1中所提到的SIR模型,對所提出的KSC指標與度、緊密性、介數和K-shell中心化指標進行了分析比較.實驗模擬傳播過程中,每次只選取網絡中的一個節點作為初始傳播節點,設定較短傳播時間(t=10),對每個節點進行1000次重復實驗取均值,最終感染與恢復的節點總數定義為影響力F(t).

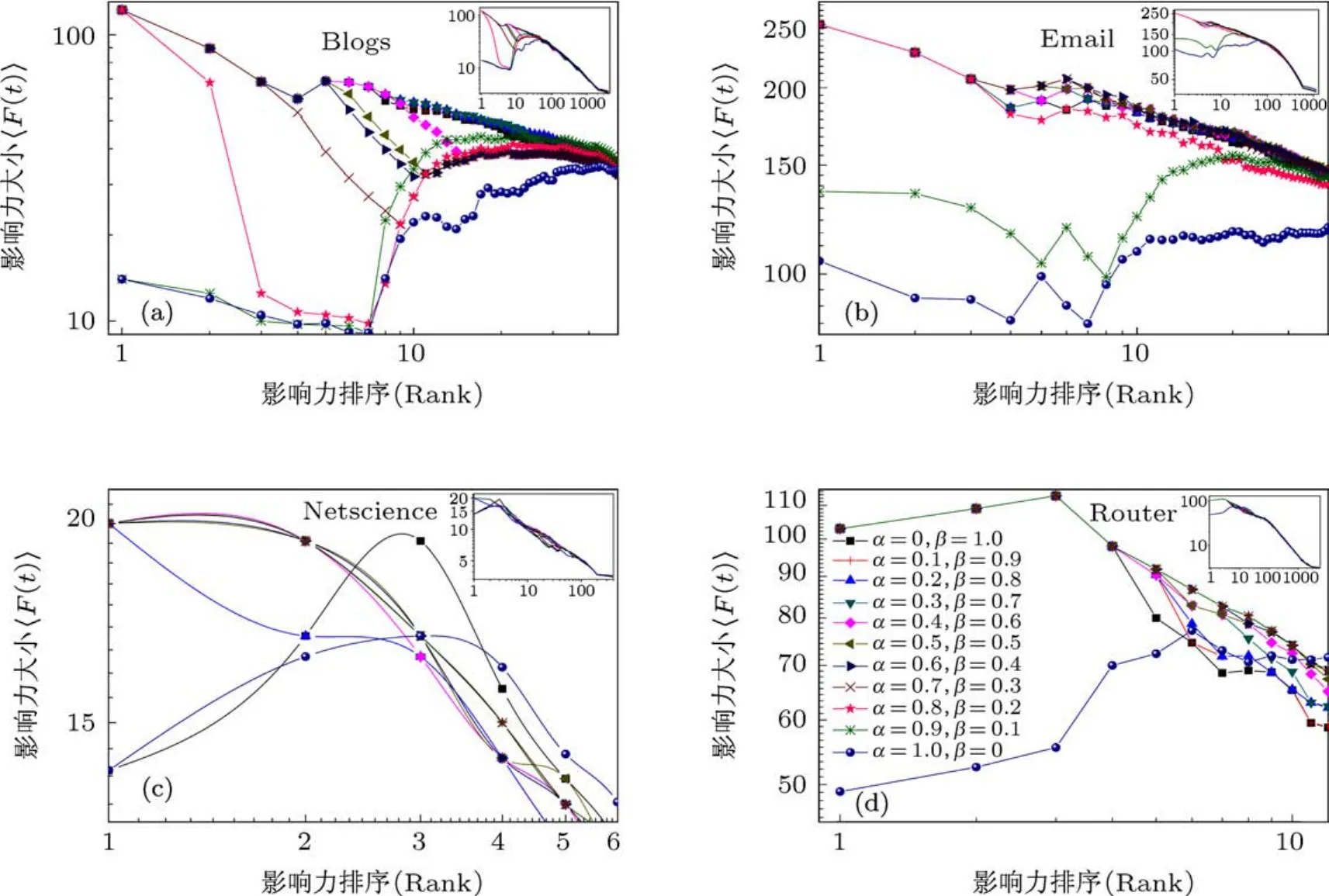
圖2 KSC模型中內部影響因子α與外部影響因子β取不同對傳播影響力指標的影響分析

圖2 表示了在KSC模型中選取不同的內部影響因子α與外部影響因子β(α+β=1)對結果的影響程度.哲學范疇中事物的運動和變化,是由它本身固有的內部矛盾引起的,又是同它所處的一定的外在條件相聯系的,內因和外因在事物發展中的地位和作用是不同的.這與模型中內部影響因子α與外部影響因子β對傳播影響假設完全一致.如在圖2(c)中局部放大了最具影響力的前10位,當0≤α≤0.2,1≥β≥0.8,或1≥α≥0.8,0≤β≤0.2時可以看到,影響力曲線波動較大,影響力排名靠后的節點影響反而大.即只是單純的考慮內部屬性或外部屬性對發現最具有影響的節點來說準確性,適用性較差.

經實驗分析得出四種不同拓撲結構網絡的內、外影響因子經驗取值情況,如表3所示.可以看出在不同類型的網絡結構中,內、外因所起的權重是不同的,本文實驗中的α,β根據表3中取較好的經驗值,這從另一方面證明了所提出模型的合理性及普遍性.

圖3所表示的是在不同的網絡中中心度指標與實際影響力之間的關系.

在Blogs網絡中,度,K-shell,介數指標與影響力F(t)關系都不是很明顯,例如在介數指標結果中,一些介數大的節點F(t)比一些介數很小的節點影響力還要低,但KSC指標可以較好地區分出最具影響力的節點.Email網絡中,所有指標表現都較好,緊密度與KSC更為理想,這與網絡的拓撲結構有關系.在Netscience網絡中,介數衡量結果最差,緊密度,K-shell與節點F(t)影響力關系也不明顯,KSC的效果要優于度數.在路由網絡(Router)中K-shell與KSC結果接近,其他指標結果很難得到傳播力較大的節點.總之,在不同的網絡中傳統的中心度指標各有優缺點,但是我們提出的KSC整體效果最好,都能有效地區分出最具有影響力的節點,通用性較強.

表3 內、外影響因子取值情況

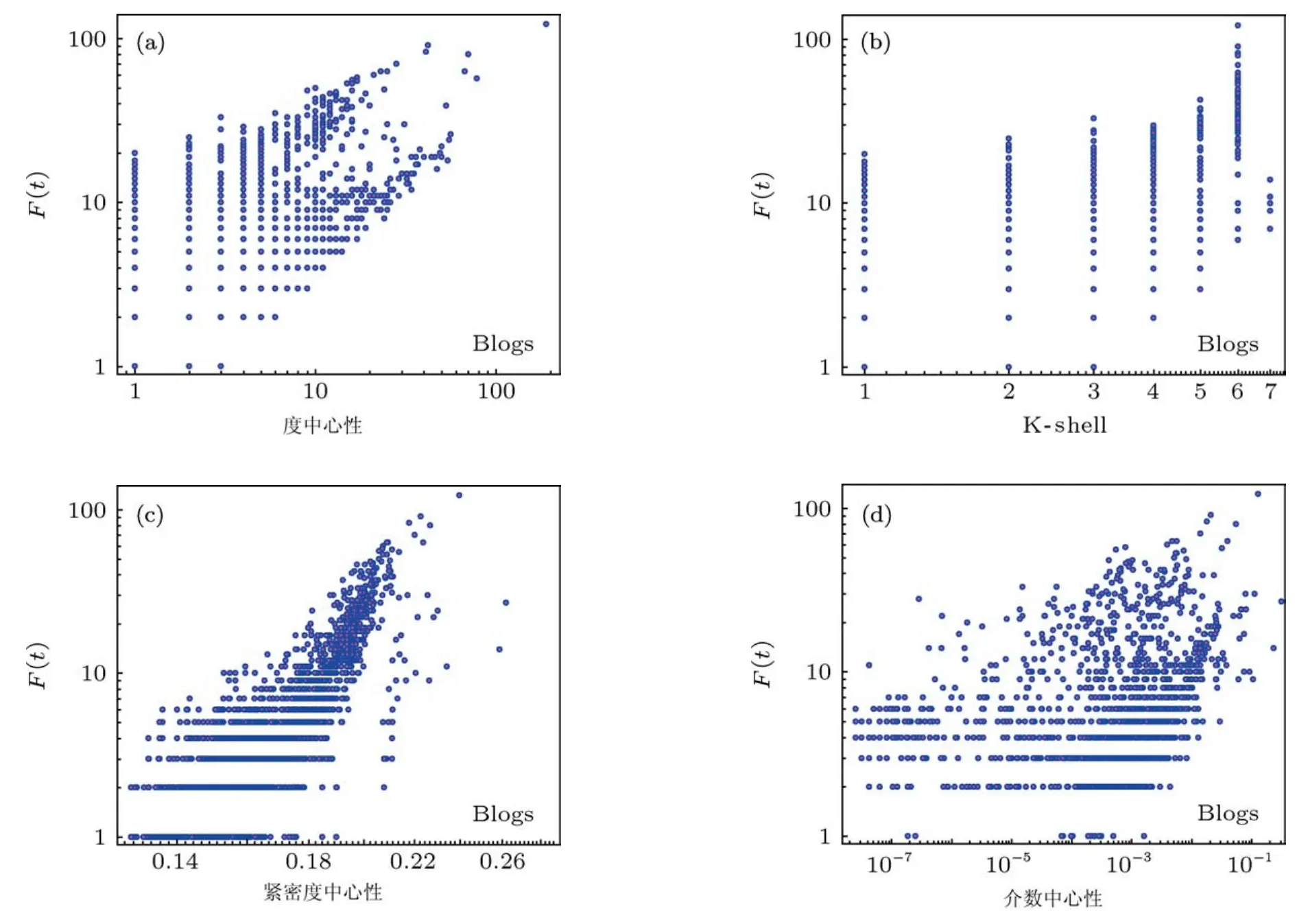
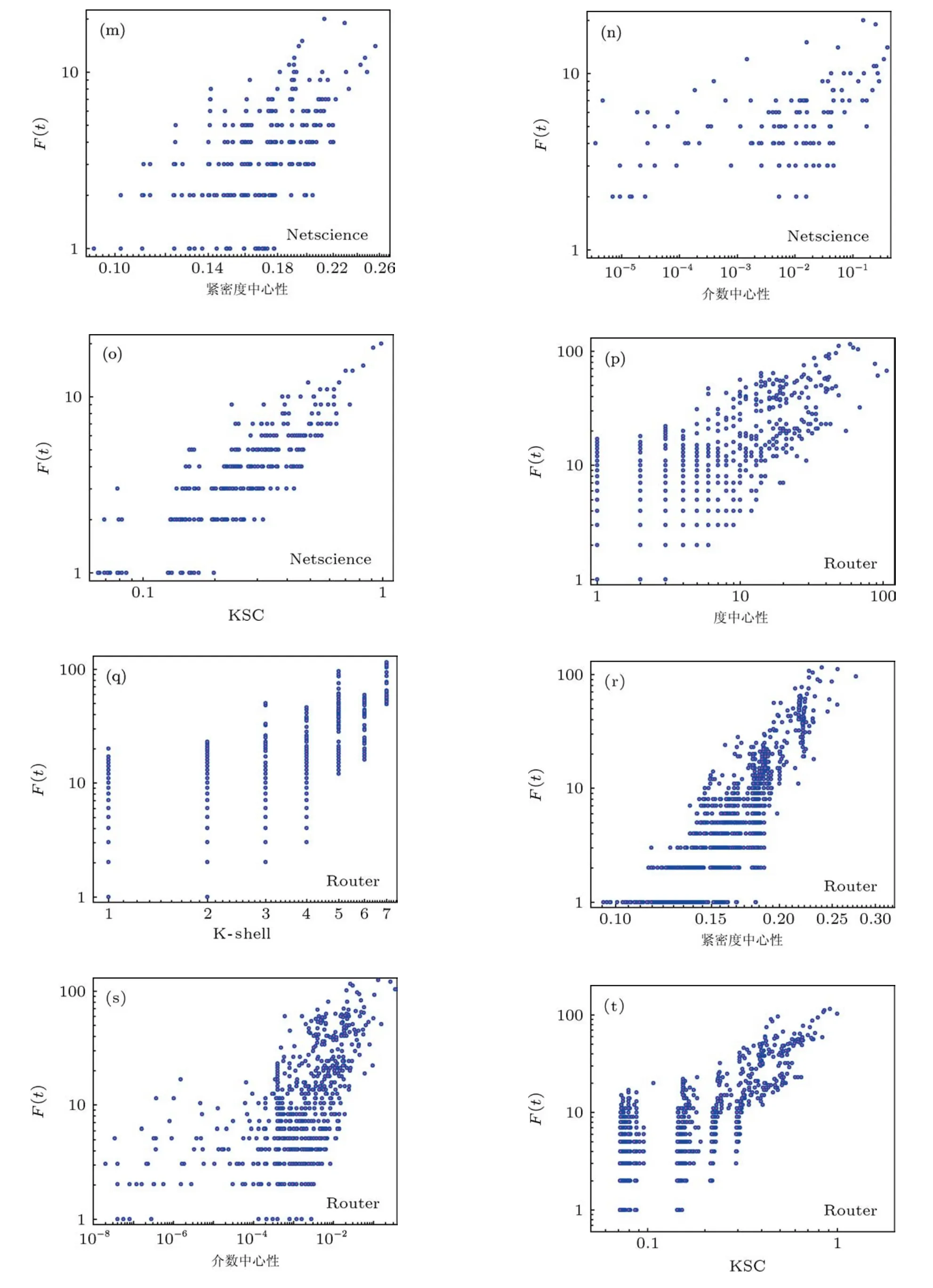
圖3 節點影響力分析比對,列代表5種不同中心化指標,行表示為4種不同的復雜網絡環境,傳播影響力F(t)(t=10),每個初始節點重復運行1000次取均值

對于單個傳播源的情形,最具有影響力的節點并非度數最大的節點或者介數最大的節點,而是K-shell最大的節點,這一結論在Kitsak等[22]已在《Nature Physics》指出.圖4比較了KSC與K-shell的實驗效果,KSC比K-shell增加了外部屬性的影響因素.例如在Email網絡中,當K-shell為10時,傳播影響力F(t)(t=10)并不穩定,而且變化范圍較大,并且影響力隨著KSC值的增大呈現增大趨勢.在4種復雜網絡中明顯可以看出當KSC一定時F(t)相對穩定,顏色變化范圍較小.

圖4 KSC與K-shell指標在4種不同復雜網絡中的分析比較,橫軸表示KSC的指標值,縱軸表示K-shell的指標值,顏色坐標代表SIR模型仿真出的實際影響力大小F(t)

圖5 比較了KSC與介數的實驗效果.可出看出在Email網絡中,KSC與介數表現正向同步較好,都能較好地發出最具影響力的節點,但在其他三個網絡環境中KSC表現明顯優于介數指標.實驗結果表明KSC方法明顯優于已有的4種典型方法.由此可見,考慮節點的外部屬性對于找出最有影響力的節點意義重大,且具有較強的通用性,驗證了我們所提出模型的合理性與普遍性.

如圖6所示,在Blogs網絡中,KSC曲線的某一點(x,y),橫坐標表示此點用KSC指標值得出的排名為x,縱坐標表示此點在SIR仿真的實際影響力為y.理論上,一個好的指標方法應該表現為向右傾斜單調下降的曲線.因為對于一個好的指標方法,如果某個節點按該指標得出的排名越靠后,其實際影響力F(t)應該隨之減小.

從圖6結果中分析,可以看到已有的4種典型方法在不同網絡中影響力均有所波動,這些方法在不同網絡中各有優劣,通用性不強,特別是在影響力前10中波動范圍最為明顯.指標值小的傳播影響力反而比指標值大的傳播影響力要大,特別是在Blogs網絡中,已有的4種指標方法結果都不太精確,而我們提出的KSC指標幾乎在所有的網絡中都符合向右傾斜單調下降的理論曲線.

本實驗充分論證了節點影響力不但由內部屬性決定,而且還與其外部屬性密切相關,說明我們提出的KSC模型的合理性及普遍適用性.

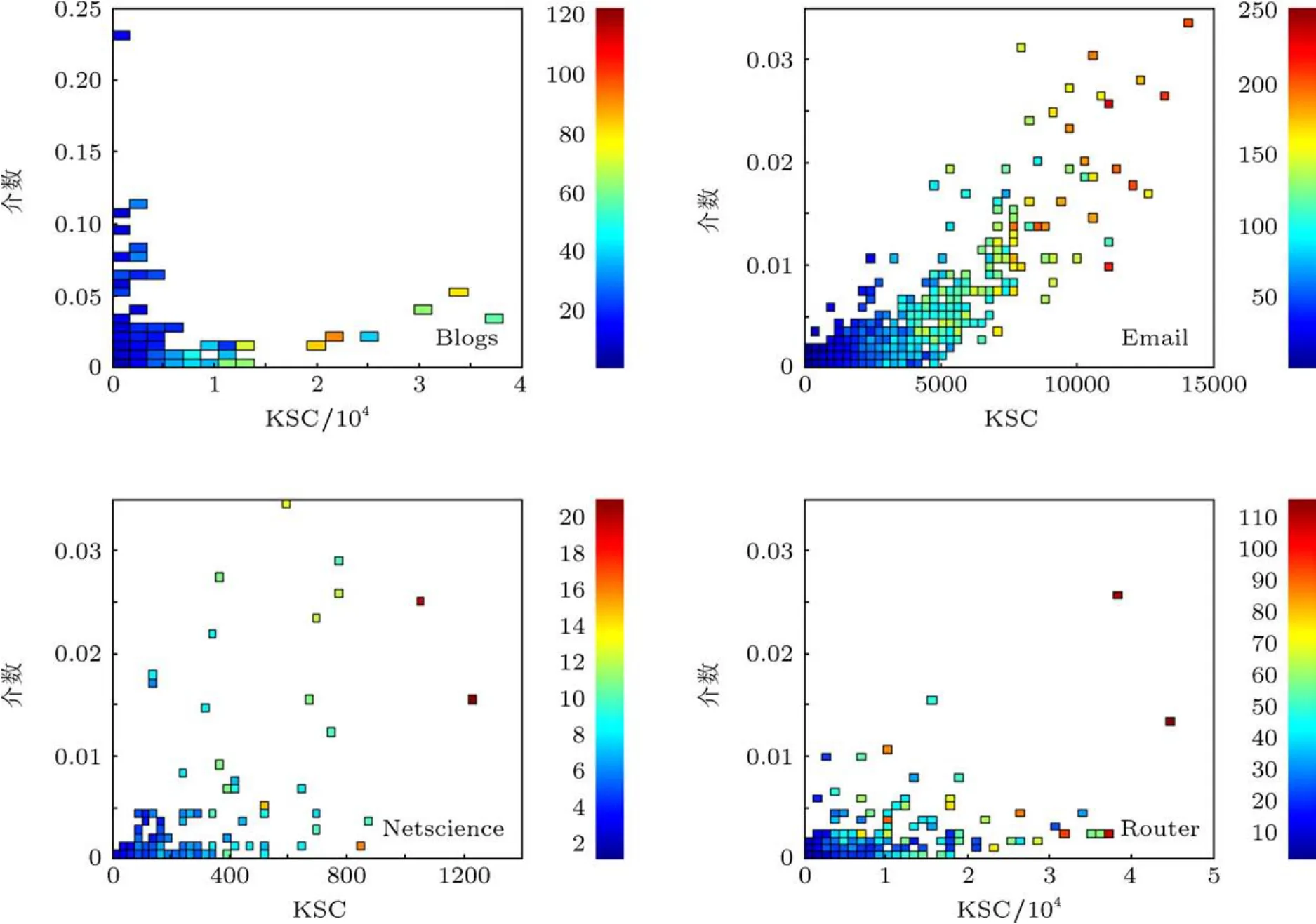
圖5 KSC與介數指標在4種不同復雜網絡中的分析比較,橫軸表示KSC的指標值,縱軸表示介數的指標值,顏色坐標代表SIR模型仿真出的實際影響力大小F(t)

5 結論

在復雜網絡中發現最具影響力的節點,可以幫助我們提高新知識、新產品的傳播效率,同時可以有效地制定相應的策略來阻止疾病及謠言傳播.復雜網絡中鑒別最具影響力的節點一直以來是研究的熱點與難點,我們提出了KSC中心化指標模型.實驗選取現實生活中常見的四種復雜網絡博客網、郵件網、路由網和科學合著網,通過SIR模型模擬節點傳播過程,并對各種中心化指標得出的影響力進行排序分析,驗證了方法的高效性和正確性.

與傳統的度、緊密度、介數和K-shell方法相比,傳統方法在不同網絡中各有優劣,通用性不強.而我們提出的KSC模型綜合考慮了節點的內部屬性與外部屬性,實驗證明用此方法鑒別節點的影響力要精確得多,適用范圍更大.我們所提出的模型為這項具有挑戰性研究提供了新的思想和方法.

感謝審稿人對本文提出的寶貴意見和建議,使得文章邏輯更加完整合理.

[1]Watts D J,Strogatz SH 1998 Nature393 440

[2]Barab′asi A L,Albert R 1999 Science 286 509

[3]Barab′asi A L,Albert R,Jeong H,Bianconi G 2000 Science287 2115a

[4]Pastor-Satorras R,Vespignani A 2002 Phys.Rev.E 65 036104

[5]Kempe D,Kleinberg J,Tardos E 2003 Proc.9th ACM SIGKDD Intl.Conf.on Knowledge Discovery and Data Mining New Washington,DC,USA,August 24—27,2003 p137

[6]Gomez-Rodriguez M,Leskovec J,Krause A 2010 Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Washington,DC,USA,July 25—28,2010 p1019

[7]Budak C,Agrawal D,El Abbadi A 2011 Proceedings of the 20th International Conference on World Wide Web Hyderabad,India,March 28—April 1,2011 p665

[8]Mislove A,Marcon M,Gummadi K P,Druschel P,Bhattacharjee B 2007 Proceedings of the ACM SIGCOMM 2007 Conference on Applications,Technologies,Architectures,and Protocols for Computer Communications Kyoto,Japan,August 27—31,2007 p29

[9]Yuan W G,Liu Y,Cheng J J 2013 Acta Phys.Sin.62 038901(in Chinese)[苑衛國,劉云,程軍軍2013物理學報62 038901]

[10]Weng J,Lim EP,Jiang J,He Q 2010 Proceedingsof the Third International Conferenceon Web Search and Web Data Mining,WSDM 2010 New York,NY,USA,February 4—6,2010 p261

[11]Xu D,Li X,Wang X F 2007 Acta Phys.Sin.56 1313(in Chinese)[許丹,李翔,汪小帆2007物理學報56 1313]

[12]Naveed N,Gottron T,Kunegis J,Alhadi A C 2011 Proceedingsof the 20th ACM International Conference on Information and Knowledge Management Koblenz,Germany,June 14—17,2011 p1

[13]Gu Y R,Xia L L 2012 Acta Phys.Sin.61 238701(in Chinese)[顧亦然,夏玲玲2012物理學報61 238701]

[14]Swamynathan G,Wilson C,Boe B,Almeroth K,Zhao B Y 2008 Proceedings of the First Workshop on Online Social Networks ACM New York,USA,August 18,2008 p1

[15]Mislove A,Marcon M,Krishna PG,Druschel P,Bhattacharjee B 2007 Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement(IMC’07)ACM New York,USA,October 24—26,2007 p29

[16]Albert R,Jeong H,Barabasi A L 2000 Nature406 378

[17]Pastor-Satorras R,Vespignani A 2001 Phys.Rev.Lett.86 3200

[18]Freeman L C 1977 Sociometry 40 35

[19]Brin S,Page L 1998 Comput.Netw.ISDNSyst.30 107

[20]Opsahl T,Agneessens F,Skvoretz J2010 Soc.Networks32 245

[21]Sabidussi G 1966 Psychometrika 31 581

[22]Kitsak M,Gallos L K,Havlin S,Liljeros F,Muchnik L,Stanley H E,Makse H A 2010 Tech.Rep.Phys.Soc.1001 5285

[23]Carmi S,Havlin S,Kirkpatrick S,Shavitt Y,Shir E 2007 Proc.Natl.Acad.Sci.USA 104 p1150

[24]Girvan M,Newman M EJ2002 Proc.Natl.Acad.Sci.USA 99 7821

[25]Fortunato S2010 Phys.Rep.486 75

[26]Newman M EJ,Girvan M 2004 Phys.Rev.E 69 026113

[27]Freeman L C 1979 Social Networks1 215

[28]Sabidussi G 1966 Psychometrika 31 581

[29]Lin K 1970 Bell Syst.Tech.J.49 291

[30]Newman M EJ2004 Phys.J.B 38 321

[31]Newman M EJ2004 Phys.Rev.E 69 066133

[32]Guimera R,Amaral L A N 2005 Nature 433 7028

[33]Burt R 2004 Am.J.Soc.110 349

[34]Granovetter M 1973 Am.J.Soc.78 1360

[35]Roy M Anderson,Robert M May 1992 Infectious Diseasesof Humans:Dynamicsand Control.(New York：Oxford University Press)p66

[36]Diekmann O,Heesterbeek JA P 2001 Mathematical Epidemiology of Infectious Diseases：Model Building,Analysisand Interpretation(New York：Wiley Seriesin Mathematical&Computational Biology)

[37]Hethcote H W 2000 Soc.Industr.Appl.Math.42 599

[38]Bernoulli D,Blower S 2004 Rev.Med.Virol.14 275

[39]Chen D B,Lu L Y,Shang M S,Zhang Y C,Zhou T 2012 Physica A 391 1777

[40]Xie N 2006 M.S.Dissertation(Bristo：University of Bristol)

[41]Newman M EJ2006 Phys.Rev.E 74 36104

[42]Spring N,Mahajan R,Wetherall D,Anderson T 2004 Acm.Sigcomm.Comp.Commu.Rev.32 3

[43]Guimer`a R,Danon L,D′?az-Guilera A,Giralt F,Arenas A 2003 Phys.Rev.E 68 065103