一類厄爾尼諾-南方濤動耦合振子動力學模型的震蕩近似解*

林萬濤 林一驊 石蘭芳 莫嘉琪

1)(中國科學院大氣物理研究所,大氣科學和地球流體力學數值模擬國家重點實驗室,北京 100029)

2)(南京信息工程大學數學與統計學院,南京 210044)

3)(安徽師范大學數學計算機科學學院,蕪湖 241003)

(2013年2月14日收到;2013年3月22日收到修改稿)

1 引言

厄爾尼諾和南方濤動(ENSO)分別是發生在熱帶大氣和海洋中的異常事件,它嚴重地影響全球各地和區預氣防為候當和前生學態術等界方所面關的注變化[1-,9對].它海的洋規和律大的氣研之究間的交互作用影響著氣候的波動,這對種交互作用的研究已經集中在厄爾尼諾-南方濤動現象上,它每隔3到4年周期地出現,并主要發生在熱帶太平洋區域.厄爾尼諾和南方濤動的振蕩性態是海-氣流動的正負兩種反饋的結果,這兩種反饋決定了海表溫度(SST)的變化,并與南方濤動流動強度有關,導致了弱信風沿著赤道行進.弱信風驅動著海洋流動變化,加強了SST的異常.海洋-大氣的正反饋與耦需合研的究不東、穩定西性太平導致洋了振子赤模道太型平的異洋溫常度關變系.化許,因多此學者已使用不同的方法對ENSO局部和整體的性態做了多方位的討論[1-6].對于復雜的全球海-氣耦合模型,通過簡化的海-氣非線性相互作用物理過程得到的振子概念模型能更容易描述海-氣耦合過程的本質和物理機理,從而能描述ENSO的某些重要物理現象.因此許多學者提出了研究ENSO的各種振子形式的動力系統模型[7-12],如“時滯振子”,“平流-反射振子”,“西太平洋振子”,“充電-放電振子”等理論的研究.本文研究一類ENSO海-氣耦合振子震動動力學模型[11].近來,許多學者研究了非線性奇攝動問題,一些近似方法被優化,包括邊界層法、平均化法、匹配近似展開方法和多重尺度法等[13-17].作者等也利用攝動理論等方法研究了一類非線性問題[18-30].本文是利用攝動理論來討論一類ENSO海-氣耦合振子.

2 ENSO耦合振子模型

考慮如下ENSO耦合振子動力學模型[7-9]：

其中T表示赤道東太平洋的SST距平,h表示赤道西太平洋的溫躍層厚度距平,C,D,E,Rh表示正參數,它們的詳細定義和物理意義參見文獻[7,8],ε為小的正參數.本文是求ENSO耦合振子動力學模型(1),(2)的震蕩近似解.

首先對方程(1)兩邊進行d/d t+Rh運算,考慮到(2)式,當C＞Rh,DE＞CRh時,可得

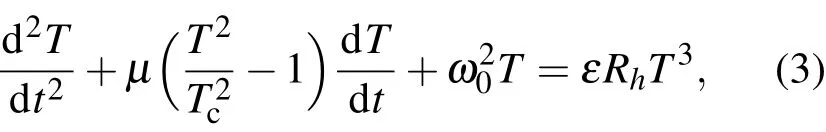
其中

由(3)式,對應的方程：

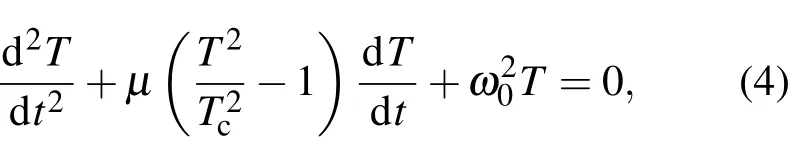
這就是van der Pol方程.由van der Pol方程的性態知,方程(4)當T＜Tc為負阻尼方程,當T＞Tc為正阻尼方程.此外,方程(4)可改寫為如下等價的平面系統：

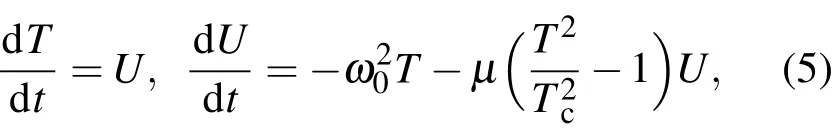
不難看出,系統(5)有一個平衡態(T?,U?)=(0,0).其對應的特征方程和特征根為

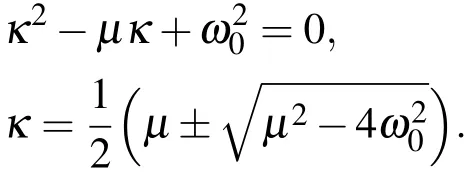
由此可知[11],當μ2＜4ω02時,即在弱阻尼的情況下,平衡態(T?,U?)=(0,0)是一個不平衡的焦點;當μ2＞4ω02時,即在強阻尼的情況下,平衡態(T?,U?)=(0,0)是一個不平衡的結點.因此,這時海-氣耦合振子當氣候稍有偏離平衡態時,將會處于不穩定狀態,并且還不難看出,當μ=0(無阻尼的情形),van der Pol方程(3)是一個Hamilton系統.當ε很小時,在無阻尼情形時,海表溫度距將做周期振蕩.當μ/=0的情形,在弱阻尼的條件下,存在兩個平衡態：一個平衡態就是(T?,U?)=(0,0),便是不穩定的焦點;另一個平衡態就是在相平面(T,U)上,是一個閉合的極限環.它是van der Pol方程在弱阻尼的情況下求得的孤立波周期解(周期吸引子),即當運動脫離平衡態后,有可能進入一個周期的運動,其周期為2π/ω0的氣候震蕩狀態.

3 ENSO模型的振蕩近似解

對于小的參數ε,在弱阻尼的條件下,我們用Krylov-Boglinbov方法來求弱阻尼方程(3)振蕩近似解.方程(3)可改寫為

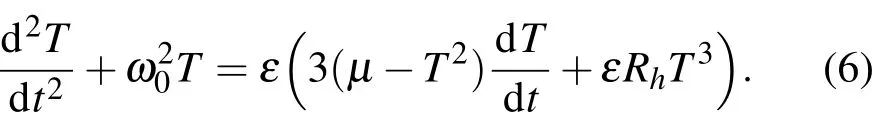
當參數ε=0時,方程(6)的解為

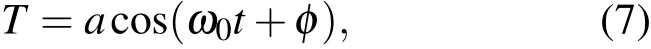
其中a,φ為常數.對于ε/=0時,我們采用廣義的“常數變易法”.將方程的解看作仍由方程(6)的形式,但a,φ為時間t的函數,且滿足條件

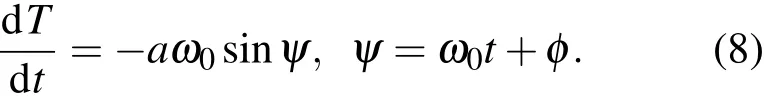
現對(7)式求導

比較(8),(9)式得

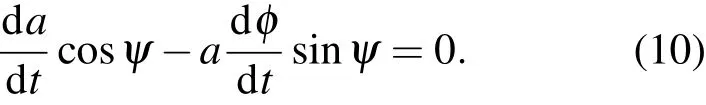
再對(8)式求導,有

將上式代入方程(6),并考慮到(7)式,得

從(10),(11)式解出 d a/d t,dφ/d t,得到

為了解(12),(13)式,注意到這些方程右邊關于變量ψ是周期函數,所以有

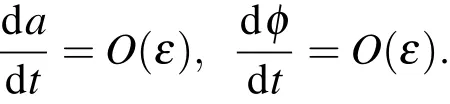
因為ε是小量,a和φ是時間t的慢變函數,所以在時間周期2π/ω0區間內它們的變化是很小的.把這些方程右邊的a和φ當作常數,在一個周期[t,t+(2π/ω0)]上求 (12),(13)式的平均值,得到

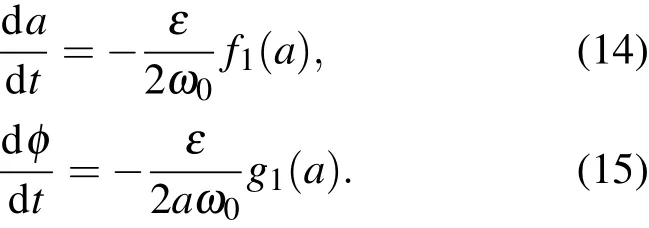
其中

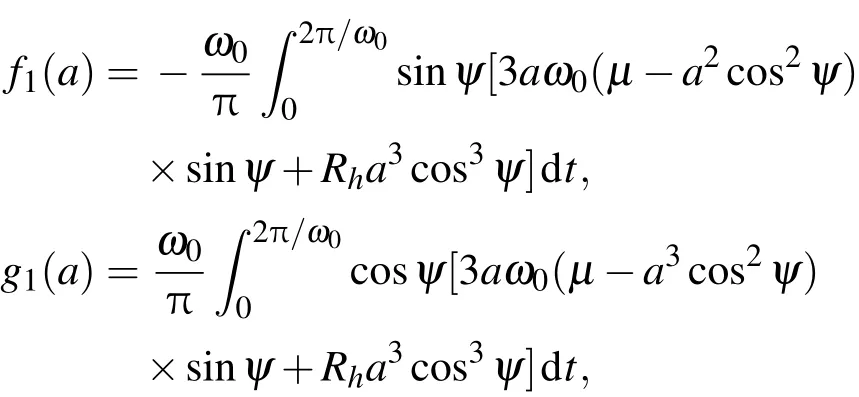
即

于是由(14)—(16)式知

積分(17),(18)式,得到

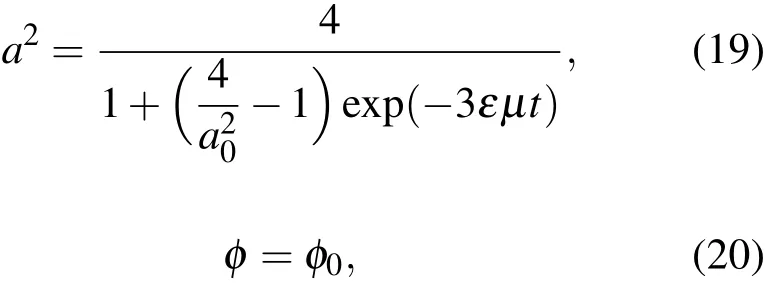
其中a0和φ0為常數.將(19),(20)式代入(7)式,我們便得到弱阻尼van der Pol方程(4)的震蕩近似解：

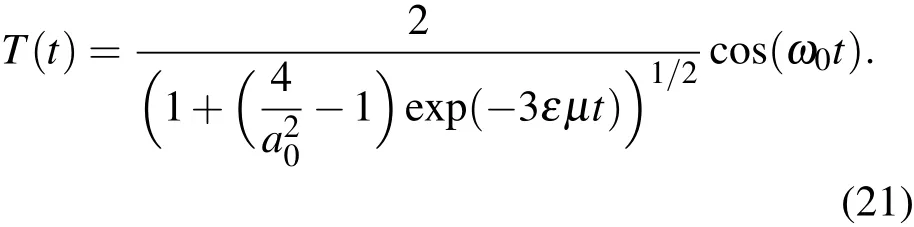
再將(21)式代入方程(2),得

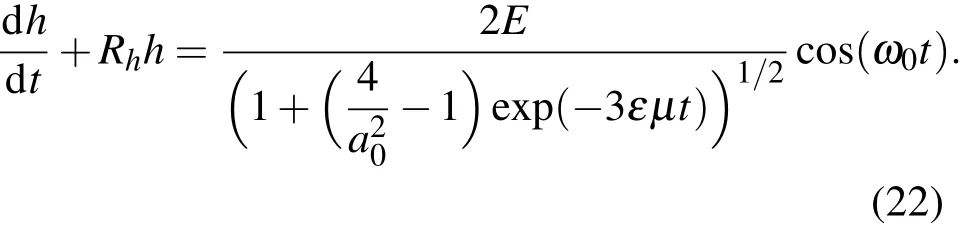
由方程(22),有解

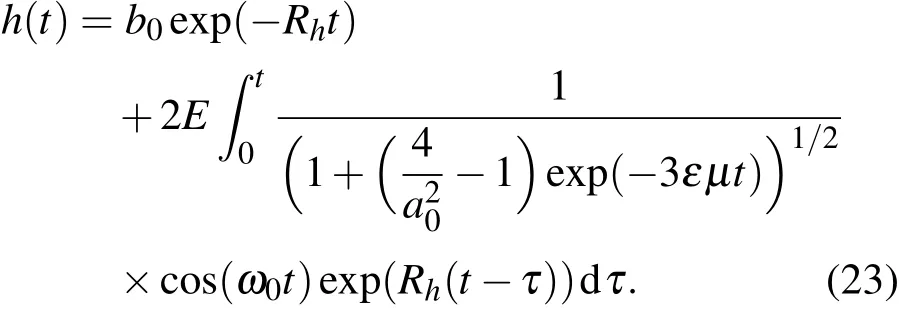
故(21),(23)式便是ENSO耦合振子動力學模型(1),(2)的震蕩近似解.用同樣的方法,還可繼續得到ENSO耦合振子動力學模型更高次的震蕩近似解.

4 舉例

現舉例說明ENSO耦合振子動力學模型解的震蕩性態.為了方便起見,我們假設如下無量綱方程：

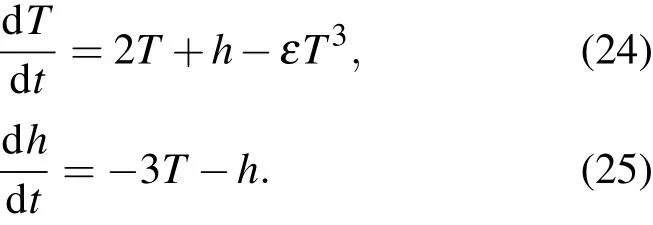
比較模型(1),(2)知C=2,D=Rh=1,E=3,μ=1,ω0=1.現求模型(24),(25)式的近似解.由(24),(25)式,對應于方程(5)為

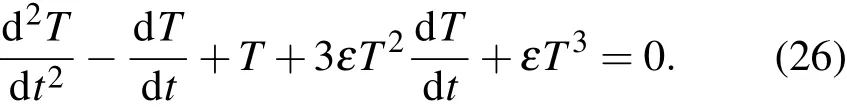
由(8)式,設方程(26)的解為

由(14),(15)式

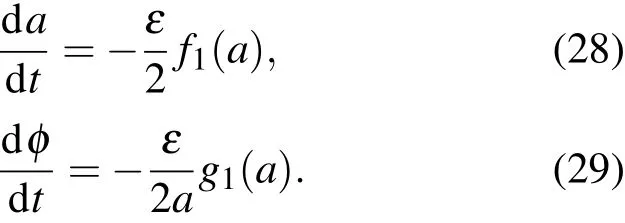
其中

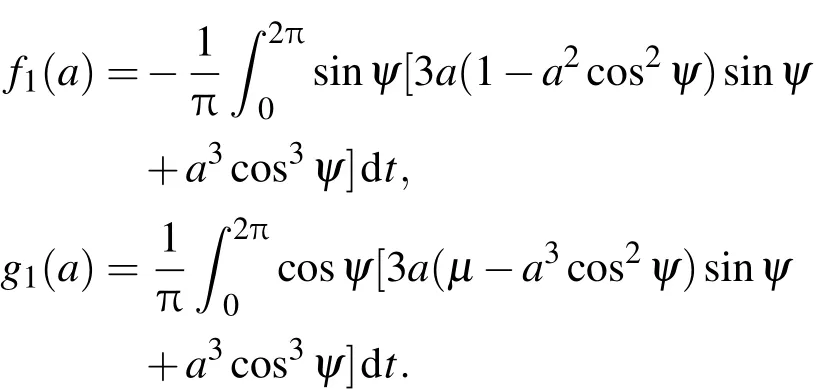
即有

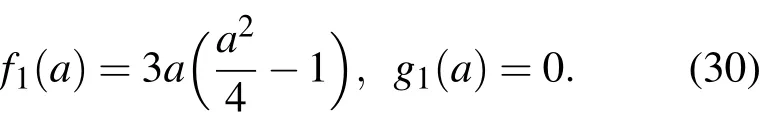
于是由(14)—(16)式知

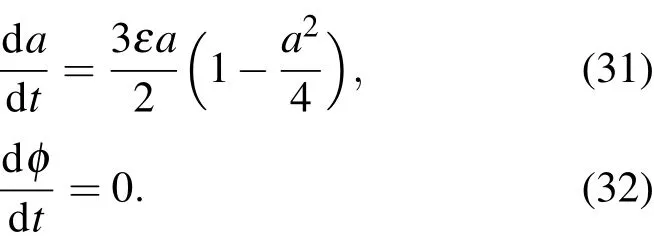
積分(31),(32)式,得到

其中a0和φ0為常數.將(33),(34)式代入(27)式,我們便得到方程(26)的震蕩近似解：

將(35)式代入方程(25),得

由方程(36),有解

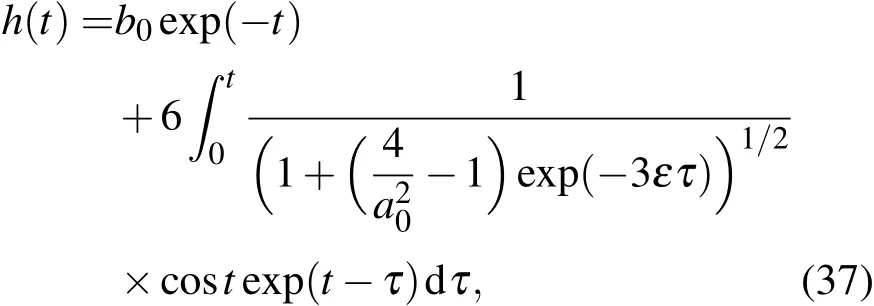
其中a0,b0為常數.故(35),(37)式便是ENSO耦合振子動力學模型(24),(25)的震蕩近似解.現設T(0)=h(0)=1,這時由解(35),(37)式得

由方程(36),有解

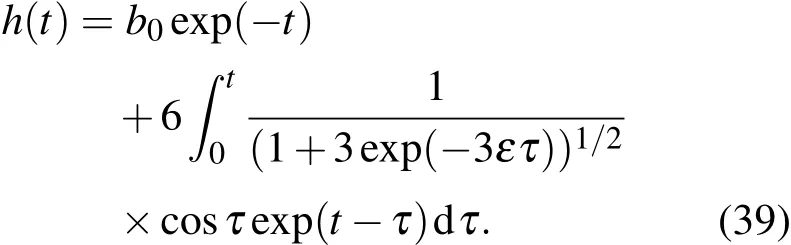
當在初始條件T(0)=h(0)=1,ε=0.5下,震蕩近似解(38),(39)曲線圖見圖1和圖2所示.由圖1和圖2可以看出,ENSO耦合振子動力學模型(24),(25)具有震蕩型的近似解.

5 結論

由于大氣物理中的復雜性,需要建立它的基本模型系統的方程,并去求解它.參數變值法和平均法是一個簡單而有效的方法.它類同于變系數非齊次常微分方程的常數變易法,但比常數變易法更深入,加上了取變量函數平均值的過程,以達到求得近似解的目的.這種方法對消去解的長期項的有界解用相應的近似解來替代很有效,同樣,這種近似解保留了解析表達式的特點,以便可以繼續對它使用解析運算.因此可以利用它對模型的相應的定性性質做進一步的探討,這對進一步了解和預測模型的有關性質更為方便和實用,特別是對大氣物理方面的氣象預報等的描述.

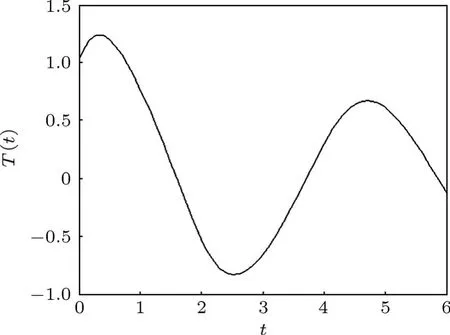
圖1 ENSO耦合振子海表溫度T(t)近似震蕩曲線圖

圖2 ENSO耦合振子溫躍層厚度h(t)近似震蕩曲線圖

[1]Feng GL,Dong WJ,Jia X J,Cao H X 2002 Acta Phys.Sin.51 1181(in Chinese)[封國林,董文杰,賈曉靜,曹鴻興2002物理學報51 1181]

[2]Guan X P,He Y H,Fan Z P 2003 Acta Phys.Sin.52 276(in Chinese)[關新平,何宴輝,范正平2003物理學報52 276]

[3]Li CG 2003 Acta Phys.Sin.52 2114(in Chinese)[李春貴2003物理學報52 2114]

[4]Li Z,Han CZ 2002 Chin.Phys.11 9

[5]Lin J,Xu Y S2003 Chin.Phys.12 1049

[6]Hu Y Q 2002 Introductory to Atmospheric Thermodynamics and Dynamics—Linear and Nonlinear Thermodynamicsof the Atmospheric Non-equilibrium State(Beijng：Geology Pub.)(in Chinese)[胡隱樵2002大氣熱力動力學導論——大氣非平衡態線性和非線性熱力學(北京：地質出版社)]

[7]Jin FF 1997 J.Armos.Sci.54 811

[8]Jin FF 1997 J.Armos.Sci.54 830

[9]Wang C 2001 1999 J.Adv.Atmosph.Sci.18 674

[10]Feng G L,Dong W J 2005 Acta Meteo.Sin.63 864(in Chinese)[封國林,董文杰2005氣象學報63 864]

[11]Zhao Q,Liu SK,Liu SD 2012 Acta Phys.Sin.61 220201(in Chinese)[趙強,劉式適,劉式達2012物理學報61 220201]

[12]Liu S K,Liu S D 2012 Nonlinear Equations in Physics(Beijing：Peking University Press)(in Chinese)[劉式適,劉式達 2012物理學中的非線性方程(北京：北京大學出版社)]

[13]de Jager E M,Jiang F R 1996 The Theory of Singular Perturbation(Amsterdam：North-Holland Publishing Co.)

[14]Barbu L,Morosanu G 2007 Singularly Perturbed Boundary-Value Problems(Basel：Birkhauserm Verlag AG)

[15]Ramos M 2009 J.Math.Anal.Appl.352 246

[16]D’Aprile T,Pistoia A 2010 J.Diff.Eqs.248 556

[17]Faye L,Frenod E,Seck D 2011 Discrete Contin.Dyn.Sys.29 1001

[18]Lin WT,Ji ZZ,Wang B 2002 Prog.Nat.Sci.12 102(in Chinese)[林萬濤,季仲貞,王斌2002自然科學進展12 102]

[19]Lin W T,Mo JQ 2004 Chin.Sci.Bull.48(suppl II)5

[20]Lin W T,Lin Y H,Mo JQ 2012 Chin.Phys.B 21 010204

[21]Shi L F,Ouyang C,Chen L H,Mo J Q 2012 Acta Phys.Sin.61 050203(in Chinese)[石蘭芳,歐陽成,陳麗華,莫嘉琪2012物理學報61 050203]

[22]Shi L F,Lin W T,Lin Y H,Mo JQ 2013 Acta Phys.Sin.62 010201(in Chinese)石蘭芳,林萬濤,林一驊,莫嘉琪2013物理學報62 010201]

[23]Mo JQ,Lin Y H,Lin W T,Chen L H 2012 Chin.Geog.Sci.22 42

[24]Mo JQ 2009 Sciencein China G 39 568

[25]Mo JQ,Lin Y H,Lin WT 2010 Acta Phys.Sin.59 6701(in Chinese)[莫嘉琪,林一驊,林萬濤2010物理學報59 6701]

[26]Mo JQ,Lin W T,Lin Y H 2011 Acta Phys.Sin.60 080202(in Chinese)[莫嘉琪,林萬濤,林一驊2011物理學報60 080202]

[27]Mo JQ 2011 Acta Phys.Sin.60 090203(in Chinese)[莫嘉琪2011物理學報60 090203]

[28]Mo JQ 2010 Commun.Theor.Phys.53 440

[29]Mo JQ,Lin Y H,Lin WT 2010 Chin.Phys.B 19 030202

[30]Mo JQ,Lin WT,Lin Y H 2011 Chin.Phys.B 20 070205