最小二乘法在熱電偶熱電勢校準中的應用

趙楠，吳方，劉丹英

(中航工業北京長城計量測試技術研究所，北京 100095)

1 問題的提出

熱電偶廣泛應用在熱處理爐控溫和溫場測試領域，這些熱電偶都需要經過計量部門校準。為了降低校準成本，使用方可以選擇幾個常用溫度點對熱電偶進行校準，其他所需溫度點的熱電動勢數值使用多項式曲線擬合法確定[1]，因此最優擬合的階次就成為研究的重點。本文通過試驗數據的比較給出了使用多項式擬合法進行熱電偶熱電勢值計算時的最佳階次，并對多項式擬合結果進行不確定度評定。

2 多項式擬合結果

依據熱電偶檢定規程[2－3]，每支熱電偶一般只檢定3～4個溫度點，以廉金屬熱電偶為例，在已知四個校準點熱電勢情況下，根據最小二乘法擬合原理，利用Matlab模擬求得一階多項式擬合、二階多項式擬合、三階多項式擬合、四階多項式擬合、五階多項式擬合、六階多項式擬合、七階多項式擬合的非校準點的實測值與擬合值的差值如表1、表2所示。其中，表1為已知N型熱電偶在550，700，830，1000℃熱電勢情況下，求得690，970，1100℃各階次多項式擬合中實測值與擬合值的差值;表2為已知K型熱電偶400，600，800，900℃熱電勢情況下，求得300，500，1050℃各階次多項式擬合中實測值與擬合值的差值。各階次多項式擬合誤差平方和如圖1、圖2所示。

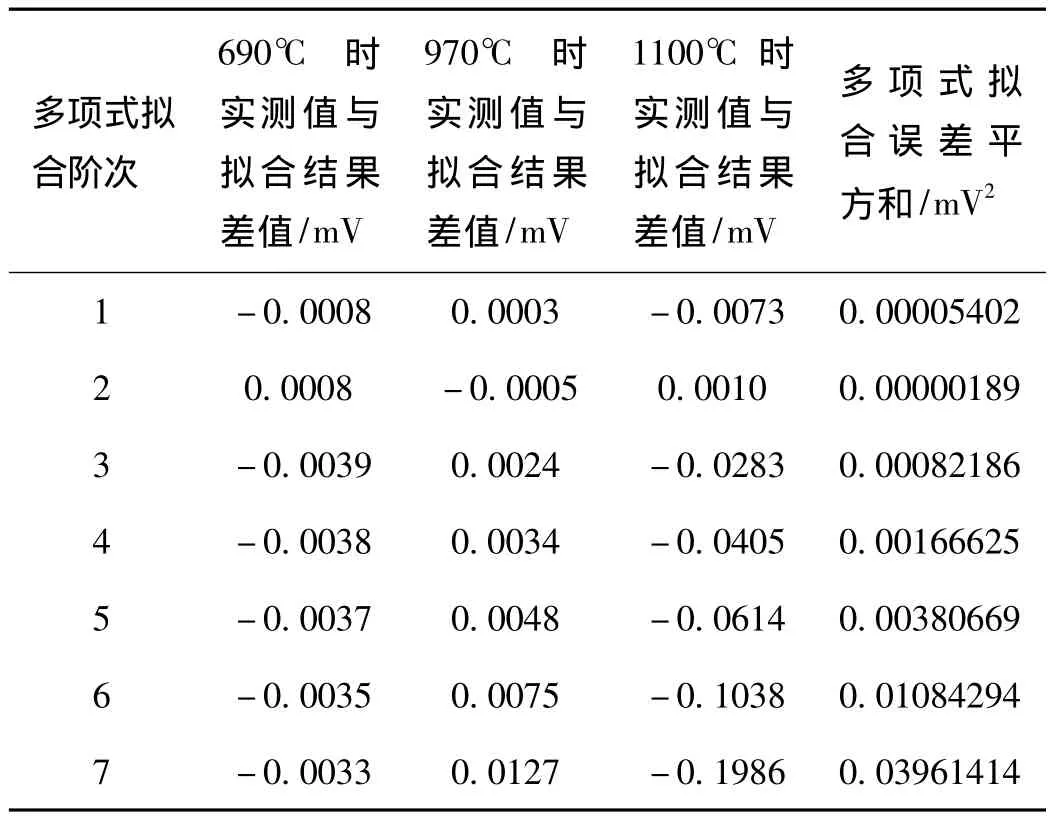
表1 N型熱電偶多項式擬合誤差表

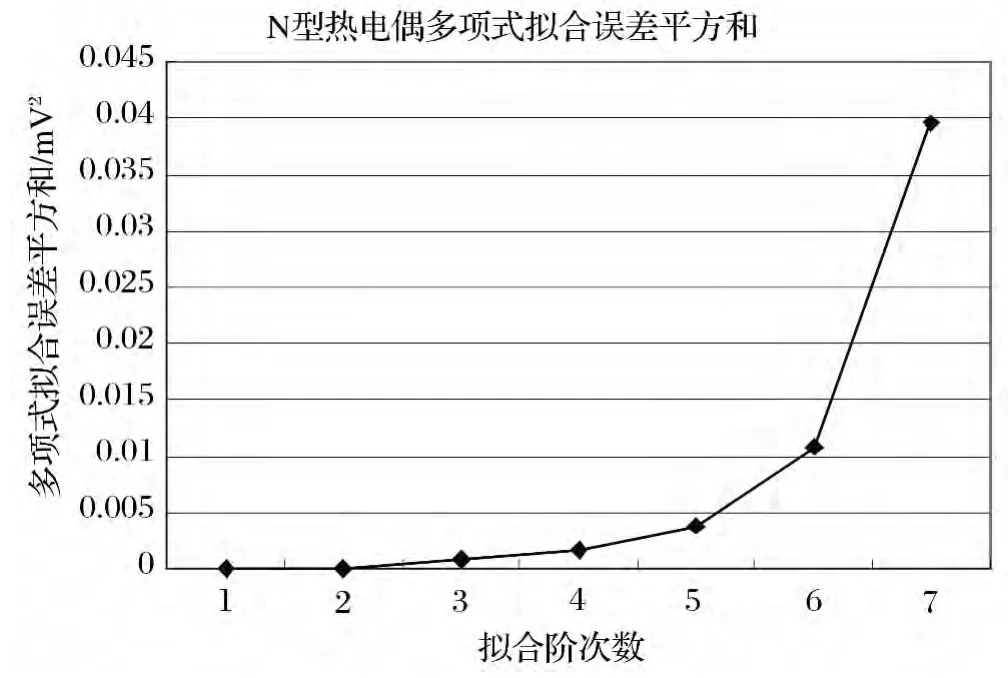
圖1 N型熱電偶多項式擬合結果分析圖

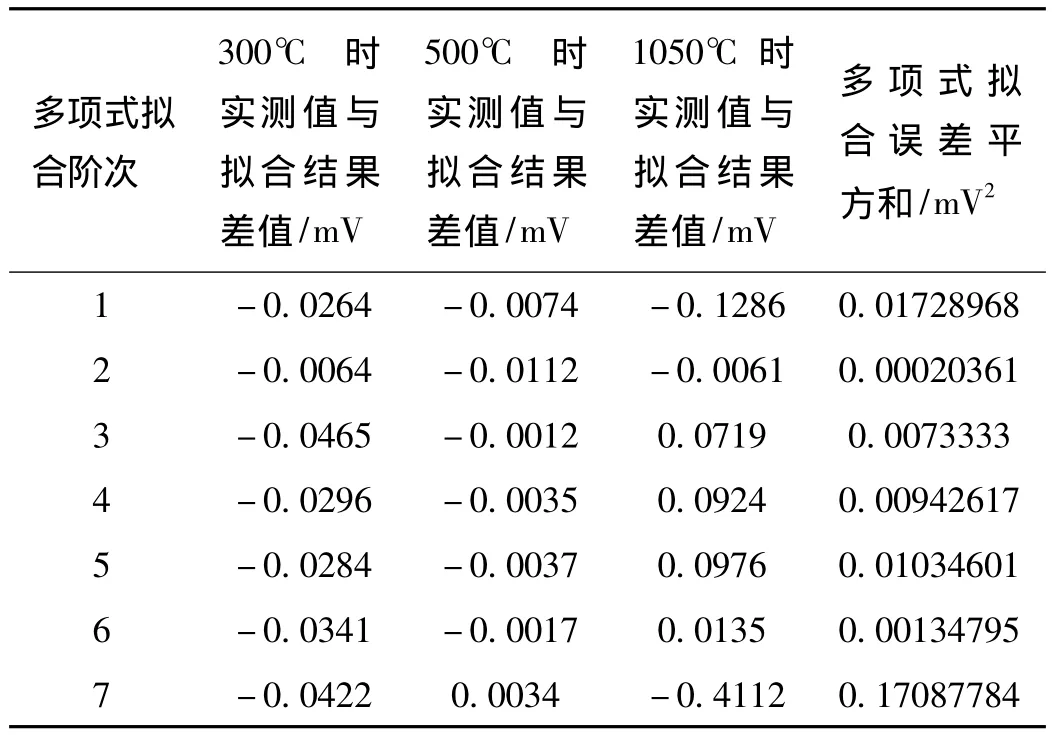
表2 K型熱電偶多項式擬合誤差表

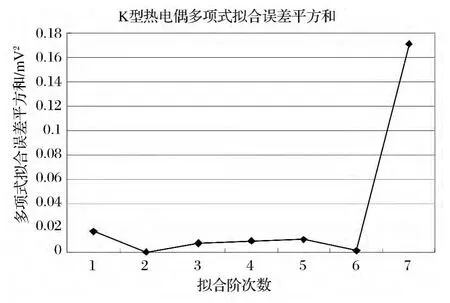
圖2 K型熱電偶多項式擬合結果分析圖

從表1、圖1和表2、圖2中可以看出:

1)利用多項式擬合曲線時，選擇二階擬合時各測試點擬合誤差的平方和最小，為最小二乘擬合的優選階次[4]。

2)利用多項式擬合曲線，內插溫度點擬合結果與實測值差別不大，外推溫度點擬合結果與實測值差別相對比較大，使用時應盡量避免使用多項式擬合方法求得外插溫度點熱電勢值。

3)在兼顧降低校準成本和保證實際使用溫度點結果可靠的情況下，只需校準使用溫度范圍的上下限及中間溫度點，利用這三個校準點求得二階擬合曲線，從而求得其他非校準點的方法是可以滿足校準需求的。

3 二階擬合結果的不確定度評定

由于目前對校準結果的表示要求越來越規范，要求每一個校準結果均應有一個不確定度與之相對應，因此需要對非校準點的擬合結果進行不確定度評定。

本文使用熱電偶測量溫度范圍的上下限及中間溫度點的校準結果，確定二階擬合曲線，求得非校準點擬合結果及其不確定度。

假設已知的三個校準點為t1，t2，t3，在這三個分度點上進行校準得到的修正值分別為 Δt1，Δt2，Δt3，而實際需要應用的分度點為t，通過二次多項式擬合得到的修正值為Δt。

所以可得

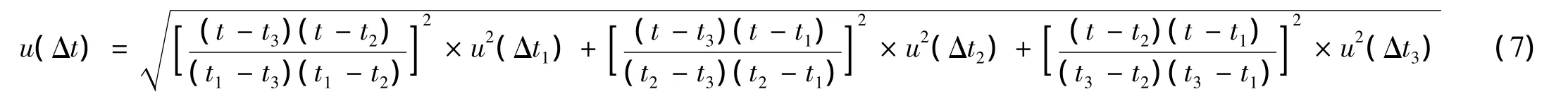
由于u(Δt1)，u(Δt2)，u(Δt3)是已知的校準溫度點，的合成標準不確定度，因此可以通過公式 (7)得出該分度點的合成標準不確定度。

4 結論

在熱電偶熱電勢校準時，利用二階多項式進行最小二乘擬合時擬合精度最高。只需在熱電偶使用溫度范圍的上下限及中間溫度點校準，并進行最小二乘擬合從而求得其他非校準點的熱電勢值，大大降低了校準成本，同時能夠保證校準數據可靠。本文同時對這一擬合結果進行了不確定度評定，這對滿足國際要求、實現每一個校準結果均應有一個擴展不確定度與之相對應具有一定的理論指導意義和實際應用價值。

[1]王建新，楊世風，隋美麗.Labwindows/CVI測試技術及工程應用[M].北京:化學工業出版社，2006.

[2]國家質量技術監督局.JJG351－1996工作用廉金屬熱電偶檢定規程 [S].北京:中國計量出版社，1996.

[3]國家質量技術監督局.JJG141－2000工作用貴金屬熱電偶檢定規程 [S].北京:中國計量出版社，2000.

[4]趙楠，劉丹英.基于最小二乘法的熱電偶特性擬合方法[J].工業計量，2013(2):45－47.

[5]馬松齡.最小二乘法在熱電偶熱電勢—溫度特性線性化中的應用[J].西安建筑科技大學學報，2001，3(1):86－88.

[6]徐耀松，付華，王丹丹.基于數字采集卡的虛擬測溫系統[J].工業控制計算機，2004，17(3):64－65.