電力數據中的冪律分布特性

王冠男，鄧春宇，趙 悅，鄭亞芹

（北京國電通網絡技術有限公司大數據業務部 北京 100070）

1 引言

在自然界和社會生活中，經常存在這樣的數據，數值在某個特征附近變化，并且變化較小，這一類數據被稱為正態分布，具有很多優秀的特性，如圖1（a）所示。比如人的身高、學生的考試成績、同質群體的紅細胞數以及數理統計中隨機誤差等都符合正態分布。在傳統數據挖掘方法中，正態分布被譽為概率論里最重要的分布。

然而，隨著大數據時代的到來，人們有能力處理完全數據而不是樣本數據，因此，現實中很多完全數據不再符合正態分布，比如個人收入的分布、變化尺度的范圍很寬，波動可以跨越很多數量級。根據這類數據可以畫出一條向右偏斜并且拖著長尾巴的累積分布曲線，顯然，它與正態分布曲線有顯著的不同，如圖1（b）所示。這種長尾分布表明，絕大多數個體的值很小，只有少數個體的值相當大。這種現象被稱為長尾效應，或者重尾法則，本文研究的冪律分布是長尾分布中重要的一種[3，4]。

研究表明，90%的電力指標數據都不符合正態分布。確定數據是否為正態分布在數據的探索性分析中具有舉足輕重的作用，因為正態分布是很多統計方法和數據挖掘方法所必需的條件，比如線性和非線性回歸模型、因子分析、典型相關分析以及主成分分析等，甚至包括最基本的線性相關性系數的計算。若數據不符合正態分布，需要采取其他相應的辦法，如數據轉換或者更換分析方法，否則輕者導致模型計算結果的不準確性，嚴重者更會影響針對算法結果所做的決策。本文主要針對電力數據中的指標進行分析，研究其真正的分布規律，主要從3個方面展開，首先介紹數據源和相關指標，然后闡述電力指標數據的冪律分布特性以及細分行業用電量的對數正態分布特性，最后結合業務背景解釋電力指標符合冪律分布的原因。

圖1 正態分布和冪律分布

2 數據描述

2.1 數據源

本文選擇全國發電量、國家電網公司售電量以及全社會用電量3個指標作為分析研究的目標，選擇原因如下。

·全社會用電量與國家經濟密切相關，研究表明，用電量的增長影響GDP的增長，而GDP的增長對用電量的增長影響不大，即用電量增長和GDP增長的關系是從用電量到GDP增長的單向因果關系。

·全國發電量是直接衡量一個國家經濟狀況的重要指標。國家電網公司是關系國家能源安全和國民經濟命脈的重要骨干企業，公司的售電量能夠反映公司甚至國家的供電能力。3個電力指標具有較強的相關性。

表1闡述了所選3個電力指標的維度、時間和區域。本文所選取的時間為2011－2013年每年的2月和7月。

2.2 電力指標的非正態分布特性

本文采取密度函數曲線檢驗法和夏皮羅·威爾克提出的W統計量，將數據和圖形相結合，共同驗證全社會發電量、國家電網售電量和全國用電量的非正態分布特性。

圖2展示了3個指標的密度函數曲線，由于空間限制，時間維度是2012年2月、2012年7月、2013年2月、2013年7月。由圖2可知，3個電力指標大多集中在較小的數值上，只有少數分布在較大的數值上，在空間維度上不符合正態分布，并且都具有長尾分布的特征。

表2～表4分別展現了2008-2013年所有2月份和7月份中3個指標的W統計量檢驗結果，即P值。

由表2～表4可知，全國發電量、國家電網公司售電量和全社會用電量的W統計檢驗的結果都小于0.05，即有不到5%的信心認為3個電力指標符合正態分布，下文將進一步分析3個指標分別符合何種分布。

3 電力指標的冪律分布特征

3.1 冪律分布特征

長尾和冪律的區別是：冪律分布需要數據必須在統計意義上可以被冪律曲線擬合，而對于長尾分布而言，能否被冪律曲線精確地擬合并不重要，重要的是有一個長長的尾巴。已知全國用電量、國家電網公司售電量和全社會發電量屬于長尾分布，但是仍需要進一步證明其為冪律分布。

表1 全國發電量、國家電網公司售電量、全社會用電量的數據描述

圖2 全國發電量、國家電網售電量和全社會用電量3個指標的密度函數曲線

表2 全國發電量的正態分布W統計量檢驗結果

表3 國家電網公司售電量的正態分布W統計量檢驗結果

表4 全社會用電量的正態分布W統計量檢驗結果

冪律分布的分布特征如圖1（b）所示，通用計算式為y=cx-r，x和 y是正的隨機變量，c、r為常數，且大于 0。冪律分布的特點是絕大多數事件的值很小，只有少數事件的值相當大。將冪律分布公式的兩邊分別取對數，則ln x與ln y存在以下的線性關系:1n y=1n c-r1n x，冪律分布在雙對數坐標下表現為一條斜率為冪指數的負數的直線，這一線性關系是判斷某個隨機變量是否滿足冪律的依據，r為冪律指數。

圖3展示了3個電力指標的冪律分布特征，時間維度是2012－2013年每年的2月份和7月份。由圖3可知，除了特殊原因引起的較小數值外（西藏地區），其他數值基本符合線性關系，并且冪律指數為正數，因此3個指標符合冪律分布的特征，屬于冪律分布。

表5～表7分別展示了3個電力指標在雙對數坐標下的參數擬合結果，其中，冪律指標r都大于-2，驗證了圖3的結論，全國發電量、國家電網公司售電量和全社會用電量符合冪律分布。

3.2 用電量的對數正態分布特征

圖3 全國發電量、國家電網公司售電量和全社會用電量的冪律分布特征

表5 全國發電量的冪律分布檢驗結果

表6 國家電網公司售電量的冪律分布檢驗結果

表7 全社會用電量的冪律分布檢驗結果

由上文可知，全國發電量、國家電網公司售電量和全國用電量符合冪律分布的特性，與其他兩個指標相比，用電量具有特殊的優良特性。

已知兩個變量X和Y無論獨立與否，X+Y的和仍然服從正態分布。若X和Y服從對數正態分布，則仍然服從對數正態分布，而X+Y卻不符合這一規律。通過分析，本文發現大部分細分行業的用電量服從對數正態分布，而細分行業用電量之和卻不符合這一規律，比如全國用電量、第一產業用電量、第二產業用電量、第三產業用電量等。在第4節中，將詳細闡述細分行業用電量服從對數正態分布的根本原因。

本文選擇具有代表性的5個細分行業進行詳細分析，分別是農業、輕工業、重工業、信息傳輸業、房地產、計算服務業。圖4展示了5個行業用電量的經驗累積分布函數（ECDF），應用極大似然估計的方法對分布參數進行擬合，并且將用電量與5個冪律分布進行對比，分別是指數分布、對數正態分布、逆高斯分布、帕累托分布和列維分布。由圖可知，對數正態分布是最合理的擬合分布。

對數正態分布的概率密度函數為：

其中：

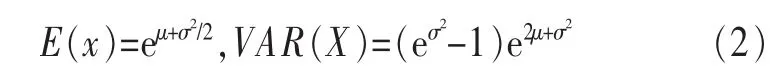
對數正態分布具有優秀的特性，當隨機變量log X符合正態分布時，則X符合對數正態分布。即對用電量進行對數轉換，就可以得到正態分布的數據，因此證明用電量符合對數正態分布不僅大大減少了數據分析的工作量，還解決了用電量不是正態分布的難題。表8展示了對數轉換后細分行業用電量的正態分布檢驗結果。

由表8可知，所有W統計量的檢驗結果大于0.05，即有95%的信心認為，細分行業的用電量經過對數轉換后服從正態分布，可以直接應用以正態分布為必要條件的數據分析和挖掘方法。

4 原因分析

由上文已知，全國發電量、國家電網公司售電量和全國用電量符合冪律分布的特性，并且細分行業的用電量服從對數正態分布，本節主要結合業務背景闡述3個電力指標符合冪律分布以及細分行業用電量服從對數正態分布的根本原因。

3個電力指標符合冪律分布特性的主要原因如下。

·由于政策、地理位置和自然環境等原因，全國經濟發展嚴重不平衡，東部沿海地區較發達，西部等地區經濟較為落后。電力和經濟密不可分，是強正相關的關系，某地區的用電情況可以反映此地的經濟狀況，因此電力指標數據在地域上也存在不平衡的現象。

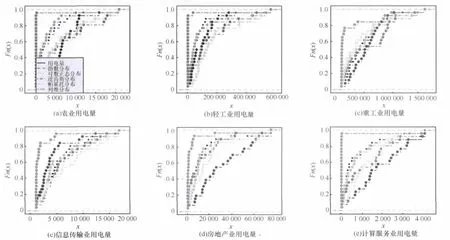
圖4 細分行業用電量的ECDF

表8 細分行業用電量對數轉換后的正態分布W統計量檢驗結果

·自然資源分布不平衡。全國的煤炭資源和水源分布不平衡，只有少數地區具有豐富的煤炭資源和水資源，這導致電力指標數據的曲線向左傾斜，并且具有冪律分布的特征。

因為電力指標數據在地域上分布不平衡，所以隨著電力指標數值的增加，P（Q>q）逐漸降低，并且降低速度減緩，呈現冪函數的規律，這正是冪律分布的特征。

細分行業用電量服從對數正態分布，下面運用數學理論闡述產生此種現象的根本原因。

正態分布的變量和對數正態分布的變量存在著區別和聯系，就共同點來說，兩種變量都是獨立變量，即用戶每天的用電量是獨立的，符合正態分布。兩種分布最大的區別在于“加”和“乘”，這種細微的不同使得數據的分布規律也具有明顯差異。

首先以布朗運動為例來解釋正態分布。假設某個行業在某一天的用電量為Q1,在下一天的用電量為Q2，在單位時間Δt內，行業用電量的差值為ΔQ，增加或者減少。令Qn為n天以后某行業的累積用電量，則：

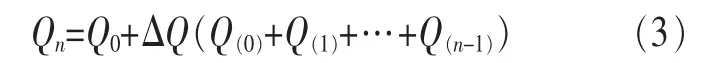
其中：

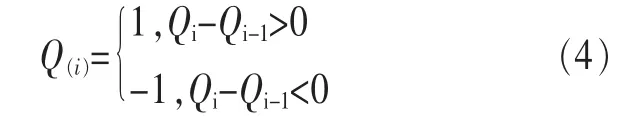
Q（i）相互獨立，且 P=1）=P=-1）=1/2。Xn服從二項分布，參數為n和p=0.5，由中心極限定理可知，當n→+∞時，Qn近似服從正態分布。

但是在現實中，由于溫度變化、某個月的假期時間長短的變化以及政策變化等原因，行業用電量的增減不是隨機的，比如通過分析發現在2月和7月，細分行業的用電量更傾向于增加而不是減少，除非發生特殊情況。假設在單位時間Δt內，行業用電量以相同的概率增加ΔQ1，減少ΔQ2，ΔQ1和 ΔQ2為已知常數，并且 ΔQ1>ΔQ2（在某些月份ΔQ1<ΔQ2，不影響最終結果）。

求解如下方程：

得到ΔQm=ΔQ1/ΔQ2。則n天以后，行業的累積用電量為：

其中，Q（i）的含義保持不變，且 P（Q（i）=1）=P（Q（i）=-1）=1/2，Q（i）相互獨立，即行業在某一天用電時不會考慮下一天的用電情況。正如布朗運動中的分析，Qn仍然服從二項分布。由于 ΔQ1>ΔQ2（或者 ΔQ1<ΔQ2），則分布曲線必定會向左偏。當n→+∞時，Qn近似服從對數正態分布。這符合中心極限定理的多重乘法的規則，即多個獨立同分布變量的乘積符合對數正態分布。因此，在同一時間段內（本文選取一個月），各個省的細分行業用電量服從對數正態分布，且如果將細分行業繼續劃分，仍然服從對數正態分布。

5 結束語

本文主要針對電力指標的分布性規律進行分析研究。經過統計分析研究發現，90%以上的電力指標不符合正態分布。經驗證，全國發電量、國家電網公司售電量和全社會用電量3個電力核心指標具有冪律分布的特性，其中細分行業的用電量符合對數正態分布，并且具體闡述了產生這種現象的業務原因和數學原因。

本文對電力指標的分布規律進行了深入研究，為電力大數據的探索性分析做出了貢獻，并且為數據分析和挖掘方法的選擇提供了理論支撐。所得的研究成果能夠為電力數據分析同行提供更多的創新思路，方法和技術也可以應用到其他電力方面的數據，不僅豐富了電力數據分析領域的技術，對很多業務問題也具有理論指導意義。不符合正態分布的電力指標數據看似毫無規律，冪律分布以簡潔優雅的形式，將毫不相干的事物聯系在了一起。以后也將是電力數據分析中研究的熱點，未來也將對電力行業中冪律分布的產生機制進行深入研究。

1 Rhee I,Shin M,Hong S,et al.On the levy walk nature of human mobility.Networking,IEEE/ACM Transactions on,2011(3)

2 Yang B,Duan W Q,Chen Z.New method to estimate scaling of power-law degree distribution and hierarchical networks.Applied Mathematics and Mechanics,2006,27(11)：1475～1479

3 葛玉偉，周戰，陳萬田.洪澤地區配電網故障冪律分布特性.現代電子技術,2011,34(6)：172～174

4 Chris A.The Long Tail.CITIC Publishing House,2005