一種任意抽取數(shù)字下變頻器的設(shè)計(jì)

袁子喬 劉 翔

(西安電子工程研究所 西安 710100)

0 引言

數(shù)字下變頻(DDC)是雷達(dá)數(shù)字接收機(jī)的重要組成部分，它位于ADC采樣芯片之后，主要功能是:對(duì)采樣后的中頻回波信號(hào)進(jìn)行混頻和濾波處理，將其變換至零中頻;對(duì)零中頻數(shù)據(jù)進(jìn)行抽取及抗混疊濾波處理，從而降低數(shù)據(jù)速率以適應(yīng)后端通用DSP器件對(duì)信號(hào)實(shí)時(shí)處理的要求。隨著芯片運(yùn)算速度的提高，大型相控陣?yán)走_(dá)采用數(shù)字波束形成(DBF)技術(shù)進(jìn)行接收波束控制成為可能，而采用DBF技術(shù)，需要大量的采用ADC和DDC通道，因此，將處理過(guò)程相對(duì)簡(jiǎn)單但運(yùn)算量巨大的DDC模塊進(jìn)行ASIC設(shè)計(jì)，對(duì)于降低相控陣?yán)走_(dá)接收通道的成本，有著非常重要的作用。

雷達(dá)在不同的工作模式下，雷達(dá)發(fā)射信號(hào)的形式和濾波器的抽取率有所不同，需要設(shè)計(jì)不同頻率響應(yīng)、階數(shù)和抽取率的低通濾波器，因此需要充分考慮不同抽取率下的低通濾波器，實(shí)現(xiàn)資源復(fù)用，造成了資源浪費(fèi)。本文基于低通濾波法提出了任意抽取率數(shù)字下變頻器的架構(gòu)，該數(shù)字下變頻器根據(jù)數(shù)字下變頻運(yùn)算的特點(diǎn)，選取合適的濾波器階數(shù)和工作時(shí)鐘，使用相同的乘法器資源則可實(shí)現(xiàn)多抽取率的數(shù)字下變頻器，實(shí)現(xiàn)了不同模式下的乘法器資源復(fù)用，較大程度節(jié)約了乘法器資源。

1 低通濾波法實(shí)現(xiàn)DDC

圖1為低通濾波法實(shí)現(xiàn)DDC的原理框圖，輸入中頻信號(hào)x(t)的中心頻率為f0，帶寬為B，A/D采樣頻率為fs，經(jīng)A/D采樣后，以數(shù)字信號(hào)x(n)的形式輸出。數(shù)字信號(hào)x(n)與正交的本振信號(hào)分別相乘，將信號(hào)分為I，Q兩路，兩路信號(hào)再經(jīng)過(guò)低通濾波抽取后，得到正交雙通道信號(hào)I(n)和Q(n);兩路濾波器系數(shù)均為 h(n)［1］。

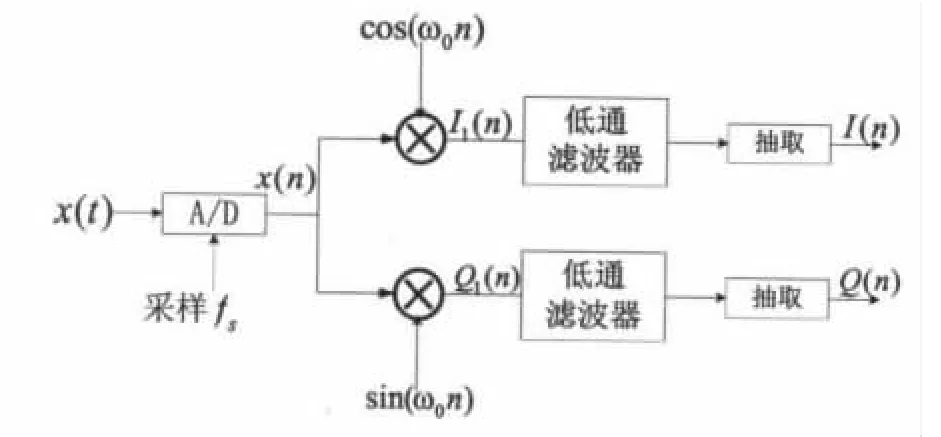
圖1 低通濾波法實(shí)現(xiàn)DDC的原理框圖

由于中頻信號(hào)中心頻率為f0，帶寬為 B，位于(fL，fH)之間，則A/D轉(zhuǎn)換器的采樣頻率fs需要滿足帶通采樣定理:，M=0，1，2，…;M 取能滿足fs≥2B的最大整數(shù)，則根據(jù)fs進(jìn)行等間隔采樣所得到的采樣信號(hào)x(n)，就能準(zhǔn)確的恢復(fù)出原始信號(hào)x(t)［2］。

假設(shè)采樣后的輸入信號(hào)為:

上式中ω0=2πf0/fs，φ(n)為中頻信號(hào)的相位信息。本振信號(hào)的頻率要求與載波頻率相等，對(duì)輸入信號(hào)分別乘以正交的本振信號(hào)，可得到:

I路:

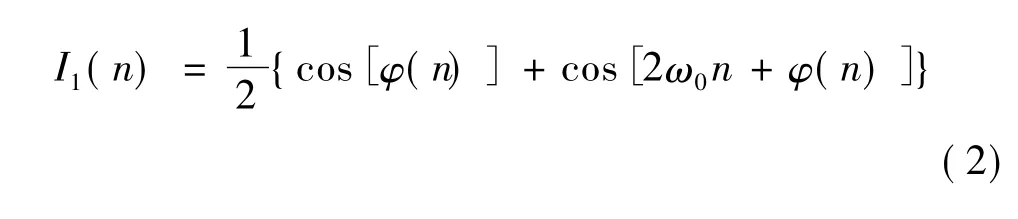
Q路:

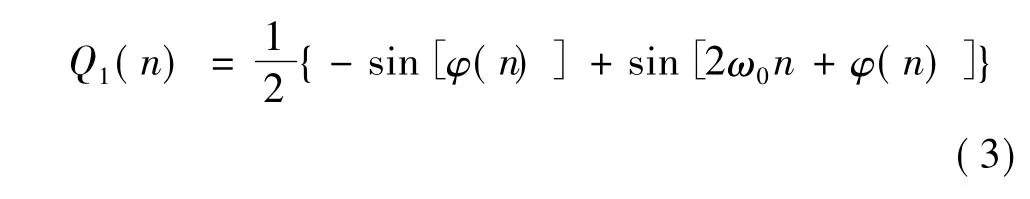
由式(2)、(3)看出:經(jīng)過(guò)數(shù)字正交混頻后，輸出信號(hào)包括了我們需要的低頻分量，以及二倍載波頻率(2ω0)的高頻成分，幅度值均為原來(lái)的二分之一。利用低通濾波器濾除不需要的高頻成分，即可得到需要的基帶信號(hào)。經(jīng)數(shù)字低通濾波器后得到的信號(hào)表達(dá)式為:

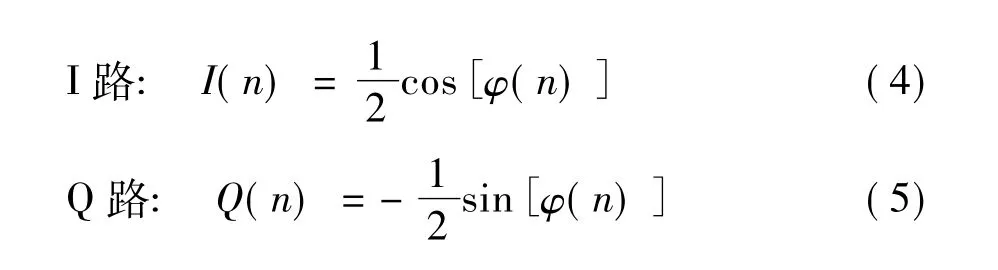
其中I(n)和Q(n)分別表示信號(hào)的同相分量和正交分量。

按照?qǐng)D1的原理框圖，設(shè)計(jì)了數(shù)字下變頻芯片的框圖如圖2所示。主要包括:數(shù)字正交混頻、任意抽取低通濾波器、系數(shù)存儲(chǔ)器、SPI控制接口。

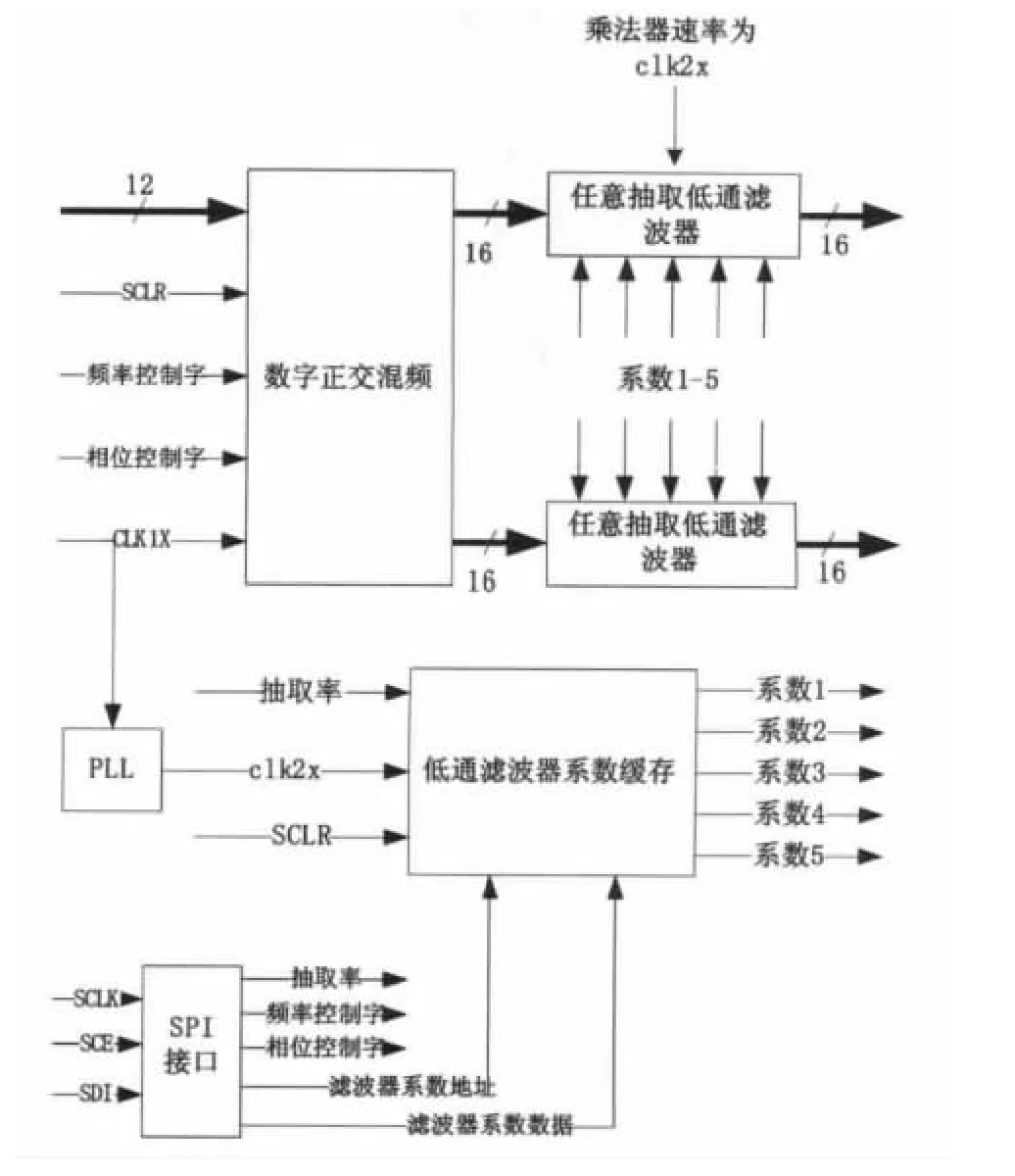
圖2 數(shù)字下變頻芯片框圖

其中SPI接口作為設(shè)置芯片參數(shù)的接口，在芯片正常工作前，實(shí)現(xiàn)對(duì)頻率控制字、相位控制字、抽取率以及低通濾波器系數(shù)的配置。

2 數(shù)字正交混頻

數(shù)字正交混頻可以采用查找表+乘法器，或者采用Cordic算法進(jìn)行向量旋轉(zhuǎn)來(lái)實(shí)現(xiàn)。基于查找表的NCO需要占用大量的ROM存儲(chǔ)器資源，才能保證一定的精度［3］。而基于Cordic算法進(jìn)行向量旋轉(zhuǎn)不需要使用存儲(chǔ)器資源，僅通過(guò)多級(jí)流水即可實(shí)現(xiàn)輸入向量的角度旋轉(zhuǎn)，如圖3所示。

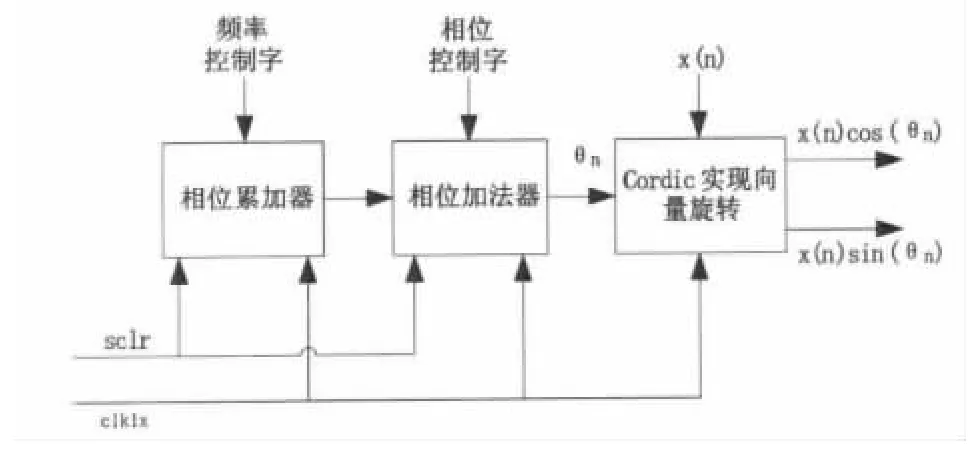
圖3 數(shù)字混頻模塊框圖

為了保證數(shù)字混頻的精確度，設(shè)計(jì)時(shí)Cordic采用16級(jí)流水線結(jié)構(gòu)，Cordic的具體實(shí)現(xiàn)參見(jiàn)文獻(xiàn)［4］。Cordic算法最大能實(shí)現(xiàn)［－99.88°，99.88°］之間的角度旋轉(zhuǎn)，而數(shù)字混頻中向量的旋轉(zhuǎn)角度范圍是［0°，360°］，因此需要進(jìn)行輸入數(shù)據(jù)和旋轉(zhuǎn)角度轉(zhuǎn)換，將向量［90°，270°］之間的旋轉(zhuǎn)角度轉(zhuǎn)化為［－90°，90°］之間的旋轉(zhuǎn)角度［4－5］。

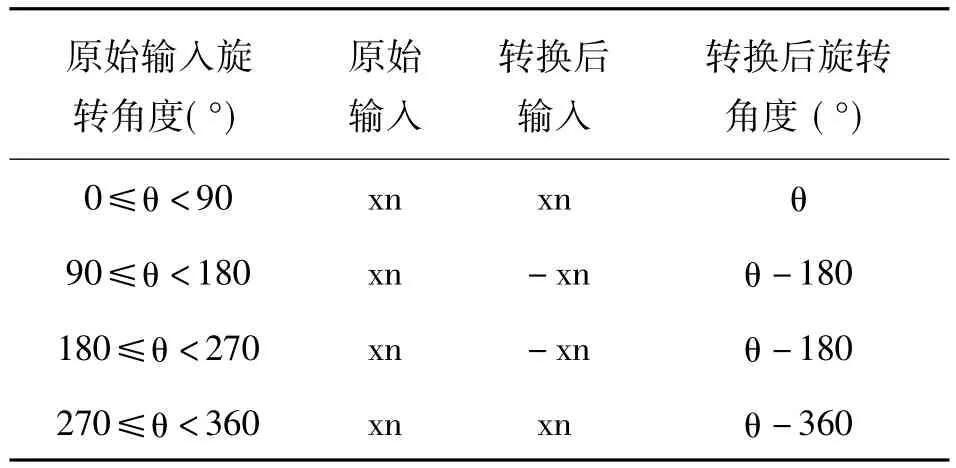
表1 輸入數(shù)據(jù)轉(zhuǎn)換表

3 任意抽取低通濾波器

從圖4可以看出，從d0至d16、d17至d32使用SRL(移位寄存器)進(jìn)行數(shù)據(jù)的延時(shí)，延時(shí)時(shí)鐘周期為抽取率，例如2抽取時(shí)，延時(shí)2個(gè)時(shí)鐘周期，10抽取時(shí)，延時(shí)10個(gè)時(shí)鐘周期，移位寄存器的深度決定最大抽取率。

反序是將輸入數(shù)據(jù)的順序以每抽取個(gè)數(shù)為一組，按照相反的順序輸出。如圖5所示的4抽取數(shù)據(jù)流，以輸入順序的自然數(shù)為例，d16為d15延時(shí)4個(gè)時(shí)鐘周期得到，而d17為d15延時(shí)4個(gè)時(shí)鐘周期，并以4個(gè)數(shù)據(jù)為一組，按輸入數(shù)據(jù)相反的順序輸出，反序部分可以采用移位寄存器或者存儲(chǔ)器來(lái)實(shí)現(xiàn)。

使用移位寄存器產(chǎn)生指定時(shí)序的數(shù)據(jù)流后，可進(jìn)入乘累加處理環(huán)節(jié)。當(dāng)濾波器系數(shù)對(duì)稱時(shí)，可通過(guò)預(yù)先加法將對(duì)稱位置的數(shù)據(jù)相加，然后與對(duì)應(yīng)的濾波器系數(shù)進(jìn)行乘累加運(yùn)算，這樣可以減少一半的乘法器資源。另外，由于輸入數(shù)據(jù)率較低，因此可以使用運(yùn)行在較高時(shí)鐘速率的乘法器，分時(shí)復(fù)用進(jìn)行乘累加運(yùn)算，乘法器運(yùn)行速率越高節(jié)約的乘法器資源也越多，一般乘法器的工作時(shí)鐘為輸入數(shù)據(jù)率的整數(shù)倍，當(dāng)然乘法器的最高工作時(shí)鐘受芯片工藝的限制，需要綜合考慮［6］。

圖6 任意抽取低通濾波器

本設(shè)計(jì)在不同抽取率情況下(見(jiàn)圖6)，輸入數(shù)據(jù)率均為clk1x，濾波器工作時(shí)鐘為clk2x，低通濾波器采用對(duì)稱系數(shù)，表2給出了不同抽取率下對(duì)應(yīng)的濾波器階數(shù)。

表2 不同抽取率對(duì)應(yīng)的濾波器階數(shù)

圖7 數(shù)據(jù)整理時(shí)序圖

如圖7所示，數(shù)據(jù)整理是將兩個(gè)clk1x數(shù)據(jù)率的數(shù)據(jù)整合為一個(gè)clk2x的數(shù)據(jù)率的數(shù)據(jù)，產(chǎn)生標(biāo)志位flag信號(hào)區(qū)分d1和d2，產(chǎn)生標(biāo)志位bypass信號(hào)標(biāo)識(shí)一組乘累加運(yùn)算數(shù)據(jù)的第一個(gè)數(shù)。

經(jīng)過(guò)乘法累加器輸出后，將數(shù)據(jù)的時(shí)鐘域從clk2x變到clk1x，降低8路求和運(yùn)算速率要求，可以采用3級(jí)流水并使用邏輯來(lái)實(shí)現(xiàn)8路數(shù)據(jù)的求和。輸出結(jié)果為輸入數(shù)據(jù)的數(shù)字下變頻結(jié)果。

4 結(jié)束語(yǔ)

本文提出了一種采用優(yōu)化結(jié)構(gòu)實(shí)現(xiàn)數(shù)字下變頻的方法。針對(duì)不同抽取率的數(shù)字下變頻，選取合適的低通濾波器階數(shù)和工作時(shí)鐘，復(fù)用相同的乘法器資源可以實(shí)現(xiàn)不同抽取率的數(shù)字下變頻處理，滿足了雷達(dá)信號(hào)處理大部分情況的使用要求，由于采用優(yōu)化的結(jié)構(gòu)盡量減小邏輯資源，降低了ASIC芯片的成本和復(fù)雜度。

［1］胡廣書(shū).數(shù)字信號(hào)處理理論算法與實(shí)現(xiàn)［M］.北京:清華大學(xué)出版社，2003.

［2］高亞軍.基于FPGA的數(shù)字信號(hào)處理［M］.北京:電子工業(yè)出版社，2012.

［3］田耘.無(wú)線通信FPGA設(shè)計(jì)［M］.北京:電子工業(yè)出版社，2009.

［4］吳曙榮.直接數(shù)字頻率合成器的設(shè)計(jì)［D］.西安:西安電子科技大學(xué)，2006.

［5］鮑景富.現(xiàn)代頻率合成技術(shù)的研究進(jìn)展［J］.電視技術(shù)，2007，47(2):1 －5.

［6］遲忠君，徐云，常飛.頻率合成技術(shù)發(fā)展概述［J］.現(xiàn)代科學(xué)儀器，2006，(3):21 －25.