乏油潤滑直齒輪傳動瞬態溫度場主要影響因素分析

2013-10-14 11:01:32丁有永朱如鵬李政民卿

機械制造與自動化 2013年5期

丁有永，朱如鵬，李政民卿

（南京航空航天大學機電學院，江蘇南京 210016）

齒輪接觸表面的摩擦熱流密度由接觸應力、齒面的相對滑動速度和齒面摩擦系數確定，其計算公式［8］為:

0 引言

在很多實際工程應用潤滑中，常常會出現潤滑油供應不足，即乏油的情況，嚴重的乏油將會使得齒輪傳動失效［1］。閆玉濤等［1～2］開展了錐齒輪乏油潤滑下穩態本體溫度場研究。王延忠等人對航空螺旋錐齒輪潤滑過程進行了分析，理論分析了輪齒表面的溫度變化［3］。龍慧等人對高速齒輪的溫度場進行了模擬，對降低輪齒溫度提出了一些方法［4］。目前，針對乏油潤滑直齒輪傳動的瞬態溫度場研究較少。

本文利用摩擦學、傳熱學、赫茲接觸等理論，給出了乏油潤滑直齒輪齒面摩擦系數、輪齒不同嚙合位置的摩擦熱流密度以及輪齒端面、輪齒齒面等區域的對流換熱系數的計算方法;建立了輪齒本體溫度場有限元分析模型，獲得了齒輪輪齒的穩態溫度場和瞬態溫度場分布，分析了潤滑油粘度、齒寬、載荷和轉速對瞬態溫度場的影響。

1 乏油潤滑輪齒瞬態溫度場主要參數計算方法

1.1 乏油潤滑齒面摩擦系數計算方法

計算乏油潤滑狀態下齒面摩擦系數的一種方法認為:乏油潤滑摩擦系數uf由邊界潤滑狀態下的摩擦系數ub與彈流潤滑摩擦系數uc共同決定的［5］，可以表示為:

式中，kc為彈流油膜的承載系數;kb為峰點接觸的承載系數，且kc+kb=1。

潤滑良好的情況下齒面摩擦系數的計算公式為［6］:

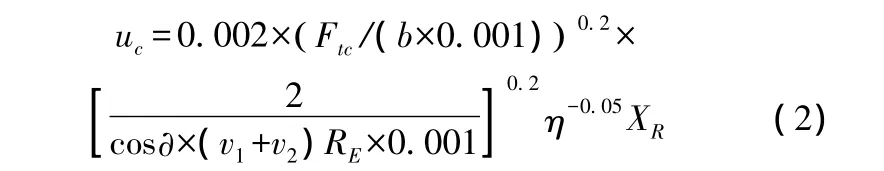
式中，Ftc為輪齒嚙合點的切向載荷，b為輪齒嚙合點處的齒寬，XR為齒面粗糙度因子，η為潤滑油的動力粘度，v1、v2分別為主、從動輪在嚙合點的速度。

邊界潤滑下線接觸齒面的摩擦系數計算公式為［7］:

式中，w為單位齒寬載荷，E為綜合彈性模量，RE為綜合曲率半徑。

將式（1）、式（2）和式（3）聯立，即可得到乏油潤滑齒面摩擦系數。

1.2乏油潤滑齒面摩擦熱流密度計算方法

齒輪接觸表面的摩擦熱流密度由接觸應力、齒面的相對滑動速度和齒面摩擦系數確定，其計算公式［8］為:

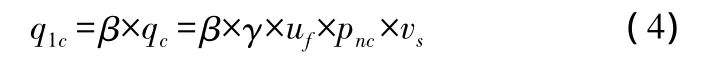
式中，q1c為摩擦熱流密度，β為熱量分配系數，γ為熱能轉換系數，uf為乏油潤滑齒面摩擦系數，pnc為嚙合點赫茲接觸應力，vs為嚙合點相對滑動速度。

嚙合過程中，當輪齒旋轉一周，在齒面各嚙合處都有一次瞬時摩擦熱流密度的輸入。假定在嚙合處的赫茲接觸區寬度為2a，則主動輪輪齒接觸區摩擦熱流密度通過此寬度的時間t1c為:

式中，a為輪齒赫茲接觸半寬，v1c為主動輪在嚙合點處的速度。

主動輪每旋轉一周所需時間t1為:

式中，n1為小齒輪轉速。

因此，主動輪每旋轉一周期，其輪齒在相應嚙合位置獲得的平均摩擦熱流密度q1ca為:

將式（4）、式（5）、式（6）代入式（7）中，即可得到平均摩擦熱流密度。

1.3 乏油潤滑輪齒表面對流換熱系數計算方法

乏油潤滑齒輪對流換熱介質為潤滑油和空氣的混合物，在計算中，將兩者混合體的熱物性參數帶入計算［9］。混合體的熱物性參數近似表示為:

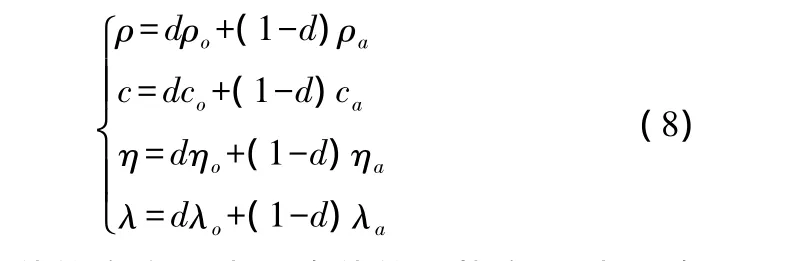
式中，ρ為混合體的密度，c為混合體的比熱容，η為混合體動力粘度，λ為混合體導熱率，帶下標“o”和“a”的分別為單向流動狀態下的潤滑油和空氣的上述熱物性參數，d為空氣和潤滑油的比例系數［10］。

嚙合齒面對流換熱系數可由下式計算:

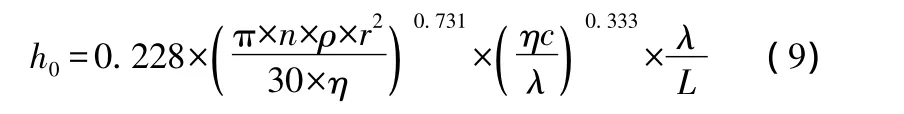
式中，n為齒輪轉速，r為齒輪分度圓半徑，ρ為混合體的密度，η為混合體動力粘度，c為混合體比熱容，λ為混合體導熱率，L為輪齒分度圓直徑。

將式（8）帶入式（9）中，即可得到乏油潤滑齒面對流換熱系數。

端面對流換熱系數可由下式計算:

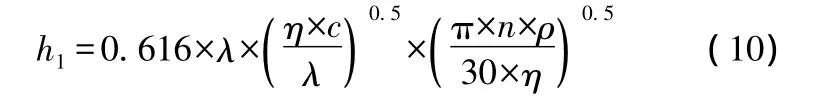
將式（8）帶入式（10）中，即可得到乏油潤滑端面對流換熱系數。

2 乏油潤滑輪齒瞬態溫度場主要影響因素分析

2.1 乏油潤滑輪齒瞬態溫度場模擬

在齒輪每轉一周的過程中，各個輪齒所經歷的過程是完全相同的。因此，在研究齒輪溫度場時，通常取單個輪齒來進行研究［6］。本文取單個輪齒進行分析，所用齒輪參數、載荷及轉速如表1所示，傳熱介質的熱物性參數如表2所示。

表1 算例齒輪傳動特征參數

表2 傳熱介質的熱物性參數

利用本文1.2節方法得出的齒面摩擦熱流密度作為熱載荷加載在嚙合齒面的表面效應單元上;利用本文1.3節方法得出的對流換熱系數作為對流載荷加載在輪齒的各個面上，可進行隨后的齒面溫度場分析。

齒輪瞬態溫度場是基于穩態溫度場的基礎上進行的，因此，先要得出齒輪的穩態溫度場。根據表1和表2的參數算出齒面加載的摩擦熱流密度和對流換熱系數，然后將平均摩擦熱流密度加載在嚙合齒面上，將對流換熱系數作為對流載荷加載在輪齒的各個面上，得出乏油齒輪傳動的輪齒穩態溫度場，如圖1所示。

圖1 乏油潤滑輪齒穩態溫度場分布等值線圖

根據圖1可知，輪齒工作齒面的溫度明顯高于輪齒的本體溫度，熱傳導使溫度由齒面到齒體呈一定梯度分布形式;齒面溫度沿齒寬方向是對稱分布，由于端面對流換熱導致輪齒端面的溫度明顯低于輪齒中部溫度;穩態齒面最高溫度出現在齒面節點偏向齒頂位置。

在穩態溫度場基礎上，計算出各個嚙合點的時間，應用載荷步將瞬時摩擦熱流密度模擬出移動熱源加載在嚙合齒面的各個節點上，得出乏油潤滑輪齒瞬態溫度場，如圖2所示。

圖2 乏油潤滑輪齒瞬態溫度場分布等值線圖

根據圖2可知，由于瞬時摩擦熱流密度輸入時間極短，輪齒齒面嚙合位置大幅升溫，但齒體溫度基本保持不變;齒面瞬時最高溫度出現在靠近齒根位置;在輪齒節圓附近也有一個峰值，與穩態溫度最大值的位置相吻合。

2.2 瞬態溫度場主要影響因素分析

a）潤滑油動力粘度的影響分析

潤滑油動力粘度對乏油潤滑齒面的摩擦系數和對流換熱系數都有重要的影響，粘度越大，齒面的摩擦系數越小，產生的摩擦熱流量也就要小，但是散熱效果較差，因此潤滑油動力粘度對乏油潤滑瞬態溫度場的影響是個復雜的過程，有必要進行分析。分析中，沿輪齒嚙合面中部徑向方向選取各個節點，在其他條件不變的情況下，得出同潤滑油動力粘度瞬時接觸齒面溫度的分布規律如圖3所示。

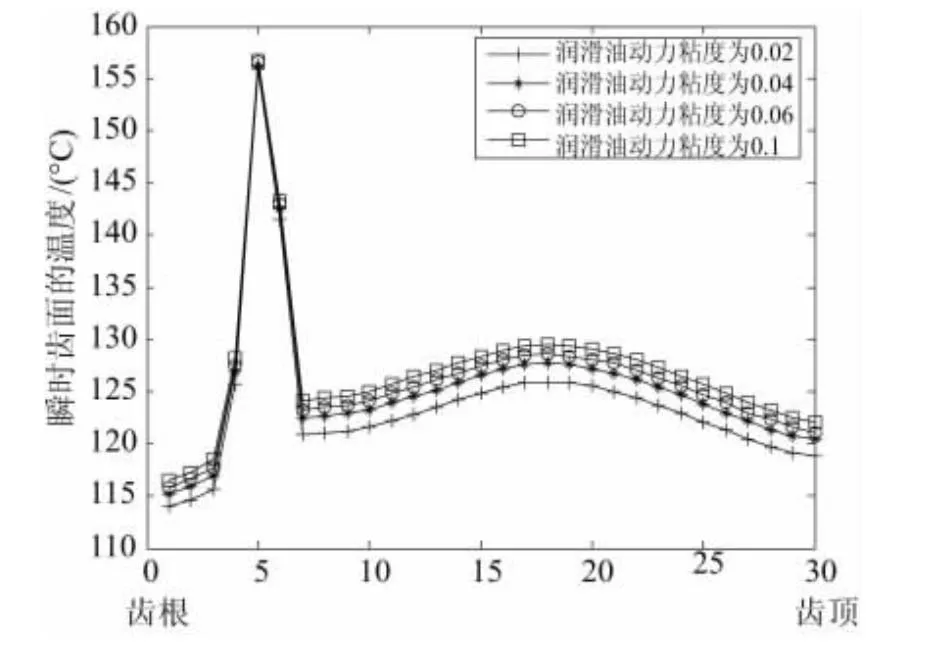
圖3 潤滑油動力粘度對瞬時接觸齒面溫度的影響

根據圖3可知，在不同潤滑油動力粘度下齒面的瞬時溫度分布規律是一致的，但隨著潤滑油粘度的增加，齒面瞬時溫度的增加很小，特別是在靠近齒根處的最大瞬時溫度位置，瞬時溫度幾乎沒有變化。主要原因是:在穩態時，由于粘度增加，齒面摩擦熱流密度減小，但是對流換熱系數也減小，導致穩態溫度有一定的升高，在計算瞬態溫度場是主要考慮瞬時摩擦熱流密度的影響，瞬時溫升最大值有一定的降低，將兩者疊加，就出現上面的情況。因此，潤滑油粘度對乏油潤滑瞬態溫度場影響很小;但在滿足其他條件的情況下，如盡量取較小值，則可以在一定程度上降低齒面瞬時溫度。

b）齒輪齒寬的影響分析

輪齒齒寬對乏油潤滑齒面摩擦熱流密度有很重要的影響，隨著齒寬的增大而減小，但是齒寬的增大卻不利于輪齒的散熱。分析中，沿輪齒嚙合面中部徑向方向選取各個節點，在其他條件不變的情況下，得出不同齒寬瞬時接觸齒面溫度的分布規律如圖4所示。

圖4 齒寬對瞬時接觸齒面溫度的影響

根據圖4可知，在不同齒寬下齒面的瞬時溫度分布規律是一致的，齒寬為14mm時的瞬時齒面溫度是最高的，但隨著齒寬的增加，瞬時接觸齒面的溫度降低，這主要是因為齒寬增大，輪齒所受的單位載荷變小，最終導致的溫度降低的影響大于對流換熱的影響。因此，減小齒寬不能降低齒面瞬時溫度，故在滿足質量等要求的情況下，應盡量選擇較大齒寬。

c）載荷的影響分析

載荷對乏油潤滑齒面摩擦熱流密度有著很重要的影響。由有限元分析知道，由于在不同載荷下，乏油潤滑齒面的瞬時溫度分布規律是一致的。因此在其他條件不變，只改變載荷的情況下，選取嚙合瞬時齒面最大溫度的變化趨勢作為輪齒瞬時溫度場的變化趨勢。輪齒齒面瞬時接觸最大溫度隨載荷變化的趨勢如圖5所示。

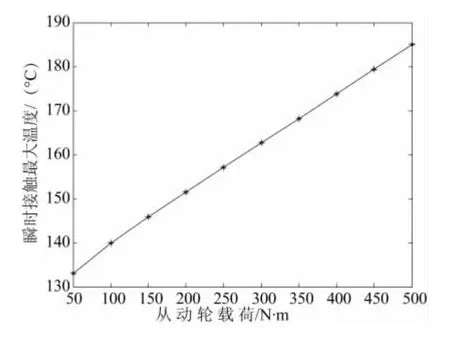
圖5 載荷對齒面瞬時接觸最大溫度的影響

根據圖5可知，瞬時接觸齒面最大溫度隨著載荷的提高一直增加，基本呈線性增長。因此，載荷對輪齒瞬時溫度場的影響非常大。

d）轉速的影響分析

轉速對乏油潤滑齒面摩擦熱流密度和齒面對流換熱系數有著很重要的影響，故轉速也是影響乏油潤滑齒輪瞬態溫度場的重要因素。分析中，沿輪齒嚙合面中部徑向方向選取各個節點，在其他條件不變的情況下，得出不同轉速瞬時接觸齒面溫度的分布規律如圖6所示。

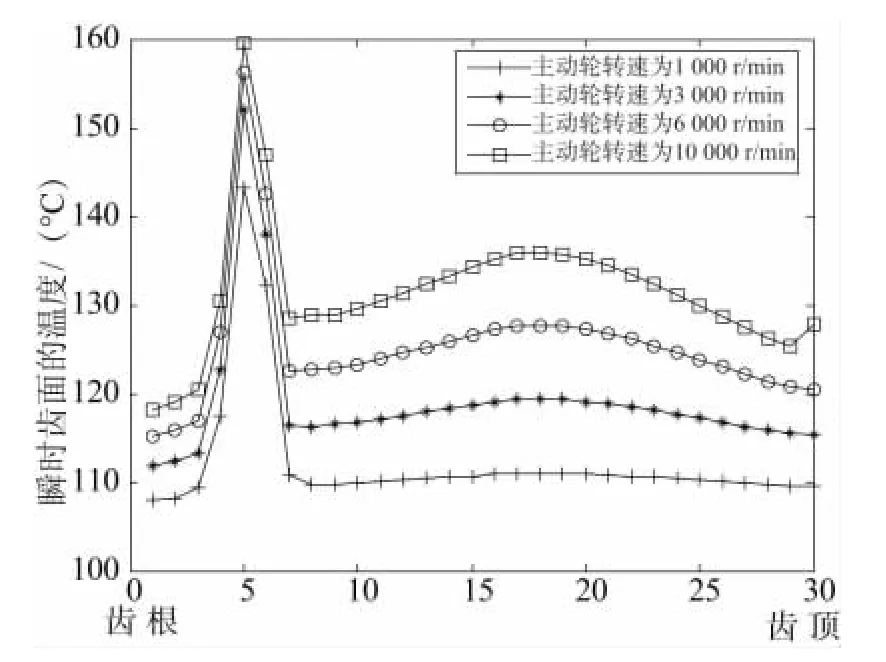
圖6 轉速對瞬時接觸齒面溫度的影響

根據圖6可知，隨著主動輪轉速的增大，瞬時齒面的溫度升高，但溫度最大值的增加卻趨于平緩，其主要原因為當轉速較大時，齒面摩擦系數會減小，導致齒面摩擦熱流量的增加量降低，最終影響溫度增加的趨勢;瞬時溫度在齒面上的分布不一致，當轉速較小時，節圓附近靠近齒頂處的溫度分布較均勻，隨著轉速的增大，該位置的溫度分布不再均勻，出現明顯的極值點。