磁懸浮機床導向導軌直線度對導向磁場力的影響分析

吳 強，錢永明，馬蘇揚，俞 冀，廖 萍

（南通大學 機械工程學院，南通 226019）

0 引言

機床導軌的導向精度是指動導軌運動軌跡的準確度，是保證導軌工作質量的前提，直接決定了機床的加工質量和生產率[1]。傳統的機床導軌由于采用接觸式導軌副，使得機床工作時導軌副之間長期存在著接觸磨損和摩擦熱變形，致使刀具與工件之間正確的相對位置發生了改變，降低了工件的加工精度[2]，因此，如何減小或消除機床導軌副工作時的磨損和摩擦以提高工件加工精度，成為機床導軌重要的研究方向之一。磁懸浮機床導軌利用電磁力實現床身導軌與工作臺導軌之間的分離，消除了傳統機床導軌工作時因接觸產生的摩擦[3]，具有無機械摩擦、無接觸磨損、無需潤滑、精度高等優點，符合現代機床導軌的發展趨勢[4]。在磁懸浮機床導軌中，導向電磁鐵與導向導軌之間懸浮氣隙的精確均勻性是決定其導向精度的直接因素，但導向導軌在加工時的加工誤差打破了懸浮氣隙的均勻性，引起導向電磁鐵電磁力偏離理論設計值，造成控制系統精度的降低，使得導向精度難以得到保障。因此，研究分析導向導軌幾何精度對導向磁場力的影響，對確定磁懸浮機床導軌的導向精度具有重要意義。本文以磁懸浮機床導軌中導向導軌的直線度為研究對象，重點分析其對導向磁場力的影響，為確定導向導軌的直線度提供依據。

1 工作原理

磁懸浮機床導軌的結構原理如圖1所示。

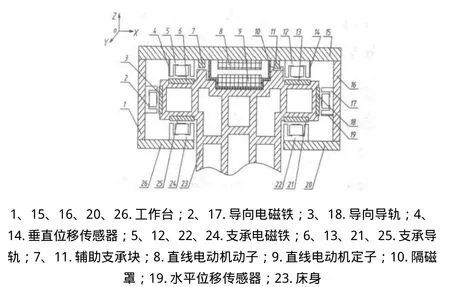
圖1 磁懸浮機床導軌結構示意圖

工作臺套裝在床身的外周，工作臺中對稱的分布著用于實現工作臺穩定支承的支承電磁鐵和精確導向的導向電磁鐵，床身中與支承電磁鐵和導向電磁鐵對應位置處分別鑲嵌著支承導軌和導向導軌。工作時，導向電磁鐵2和17、支承電磁鐵5和24以及12和22分別成對使用，每對使用一個控制器，并采用差動控制技術。當工作臺空載懸浮時，導向電磁鐵2、17所產生的電磁力大小一致，即[5]：

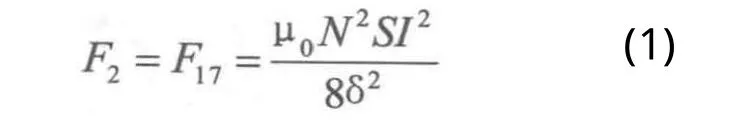
式中：μ0為真空磁導率；N為線圈匝數；S為導向電磁鐵的總磁極面積；I為偏置電流；為工作臺穩定懸浮時導向電磁鐵與導向導軌之間的懸浮氣隙值。

若某一時刻在導向方向上出現一擾動力，使工作臺向左偏離平衡位置x，經水平位移傳感器檢測傳送給控制器后，控制器發出一控制電流ic（如圖2所示），使得導向電磁鐵2和17的電磁力分別增大和減小，使得工作臺迅速回到平衡位置，即[6]：

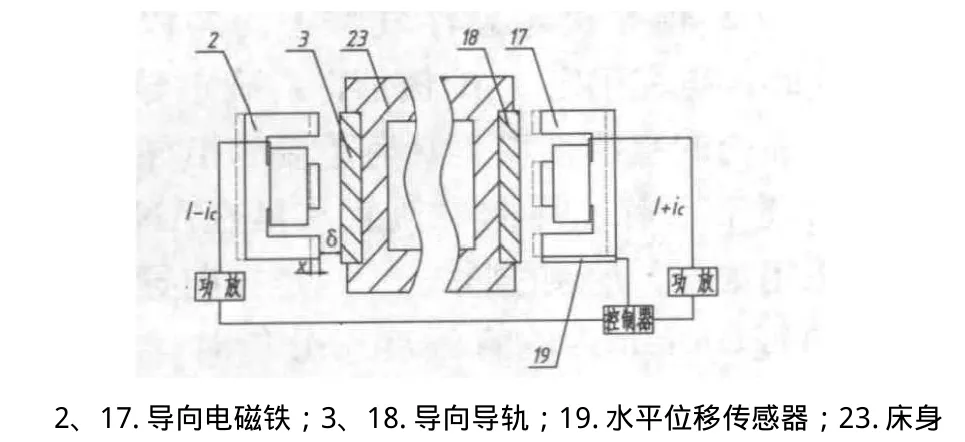
圖2 導向電磁鐵控制系統原理圖

在支承方向上，由于要承受工作臺的自重，因此，工作臺空載懸浮時，下支承電磁鐵所產生的電磁力要大于上支承電磁鐵所產生的電磁力，以支承電磁鐵5、24為例，兩者產生的電磁力分別為：

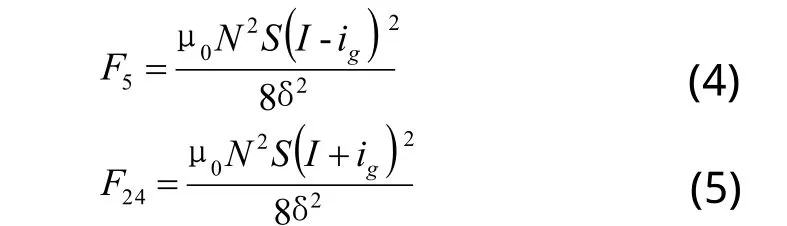
式中：ig為克服工作臺重力的控制電流。

當工作臺在支承方向上出現一擾動力時，由垂直位移傳感器檢測后傳送給控制器，再由控制器發出控制電流使得工作臺迅速回到平衡位置，其控制系統的工作原理與導向電磁鐵的控制原理一致。

直線電動機的動子安裝在工作臺的中心線上，其定子安裝在與動子相對應的床身上，直線電動機外周設置有隔磁罩。待工作臺在支承和導向方向上均實現穩定懸浮后，直線電動機通電，由其動子帶動工作臺實現直線進給運動。工作臺不工作時，由輔助支承塊對其進行支承。

2 磁懸浮機床導向導軌直線度對導向磁場力的影響分析

圖3、圖4分別為磁懸浮機床導軌中導向導軌分別在垂直和水平平面內直線度的示意圖，Δ1和Δ2值是導向導軌分別在垂直和水平平面內全長上的直線度[7]。由圖3、圖4可知，導向導軌在垂直和水平平面內的直線度誤差均將打破導向電磁鐵與支承導軌之間懸浮氣隙的均勻性，使得實際導向電磁力偏離理論設計值，造成磁懸浮機床導軌導向精度的降低，因此，需對兩者分別進行分析。

圖3 導向導軌在水平平面內直線度的示意圖

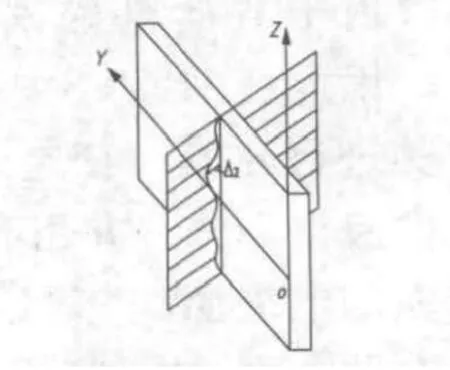
圖4 導向導軌在垂直平面內 直線度的示意圖

2.1 磁懸浮機床導向導軌水平平面內直線度對導向磁場力的影響分析

由圖3可知，導向導軌在水平平面內的直線度打破了導向電磁鐵與導向導軌之間懸浮氣隙的均勻性，而Δ1值是決定懸浮氣隙不均勻程度直接因素，因此，研究確定Δ1的極值，對確定導向導軌的在水平面內的直線度誤差具有重要的指導意義。

根據磁懸浮系統的特征，工作臺中導向電磁鐵的技術參數選擇如下：I=1A，N=192，S=400mm2，δ=0.3mm，最大控制電流icmax=1A，根據式(2)、式(3)可知，當ic為最小值0A時，導向電磁鐵2、17,的電磁合力為0，此時兩導向電磁鐵均產生25N的電磁力；當ic為最大值1A時，導向電磁鐵2、17所產生的電磁合力為100N，即所設計的工作臺在導向方向上所能承受的最大擾動力為100N，此時，兩導向電磁鐵所產生的電磁力分別為100N和0N，即導向電磁鐵所產生的最大電磁力為100N，為滿足導向導軌直線度對所有導向電磁力的使用要求，取導向電磁鐵所產生電磁力的極值100N為例，分析導向導軌的直線度對導向磁場力的影響。為便于求解，導向導軌直線度在ANSYS中的建模采用如圖5所示的形式：

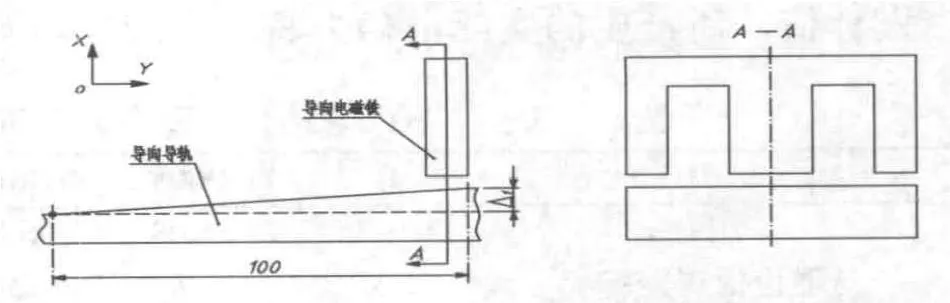
圖5 利用ANSYS對導向導軌在水平平面內直線度建模示意圖

如圖5所示，Δ1是導向導軌在水平平面內每100mm內的直線度，分析時，將導向電磁鐵設置在直線度的最大位置處，若導向電磁鐵在該位置的導向磁場力符合系統設計要求，則可確定出導向導軌在水平平面內直線度的極值。根據直線度的定義，Δ1可為正值或負值，兩者對導向電磁力將產生不同的影響，因此要分別對兩者進行分析。

由于導向電磁鐵和導向導軌的結構較為簡單，因此在ANSYS中選擇三維實體單元SOLID96對其進行建模，在定義完各項材料屬性后，進行自由網格劃分，并用有限元啞元SOURC36定義出線圈的電流源[8]，得出如圖6所示的導向電磁鐵和導向導軌的網格劃分圖。

圖6 導向導軌在水平平面內直線度的ANSYS建模圖

在完成上述步驟后，通過施加邊界條件求解后，得出了ANSYS虛功力求解的單個導向電磁鐵在結構參數及通電電流相同的情況下，其實際磁場力大小隨Δ1值變化而變化的情況，分別如表1、2所示。

由表1、表2可知，Δ1值為0時，基于ANSYS虛功力求解的單個導向電磁鐵所產生的磁場力為101.35N，與理論計算值100N的誤差為1.35%，證明ANSYS求解正確。當Δ1值為正時，導向電磁鐵與導向導軌之間的實際懸浮氣隙值小于理論設計值，所產生的實際電磁力將大于理論設計值100N，當Δ1值達到0.0005mm/100mm時，導向電磁鐵所生產的實際電磁力將急劇增大，與理論計算值的誤差超過了5%；當Δ1值為負時，導向電磁鐵與導向導軌之間的實際懸浮氣隙值大于理論設計值，所產生的實際電磁力將小于理論設計值100N，當Δ1值達到-0.0010mm/100mm時，導向電磁鐵所生產的實際電磁力將急劇減小，與理論計算值的誤差超過了5%。因此，導向電磁鐵在加工時，應將其在水平平面內的直線度控制在-0.0010~0.0005mm/100mm內。

2.2 磁懸浮機床導向導軌垂直平面內直線度對導向磁場力的影響分析

由圖4可知，導向導軌在垂直平面內的直線度也打破了導向電磁鐵與導向導軌之間懸浮氣隙的均勻性，而Δ2值是決定懸浮氣隙不均勻程度直接因素，因此，研究確定Δ2的極值，對確定導向導軌的在垂直面內的直線度誤差具有重要的指導意義。

為便于求解，導向導軌直線度在ANSYS中的建模采用如圖7所示的形式，Δ2是導向導軌在垂直平面內每100mm內的直線度，分析時，將導向電磁鐵設置在直線度的最大位置處，若導向電磁鐵在該位置的導向磁場力符合系統設計要求，則可確定出導向導軌在垂直平面內直線度的極值。根據直線度的定義，Δ2可為正值或負值，兩者對導向電磁力將產生不同的影響，因此要分別對兩者進行分析，其技術參數以及在ANSYS中的求解過程與2.1節所述一致。

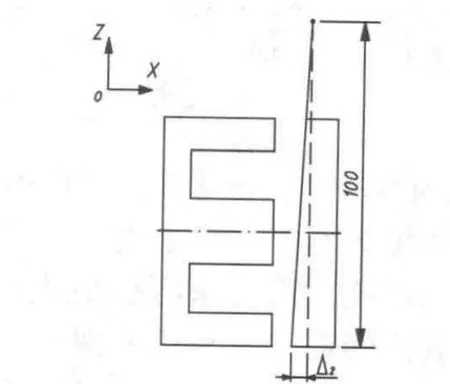
圖7 利用ANSYS對導向導軌在垂直平面內直線度建模示意圖

表3、表4列出了基于ANSYS虛功力求解的單個導向電磁鐵在結構參數及通電電流相同的情況下，其實際磁場力大小隨Δ2值變化而變化的情況。

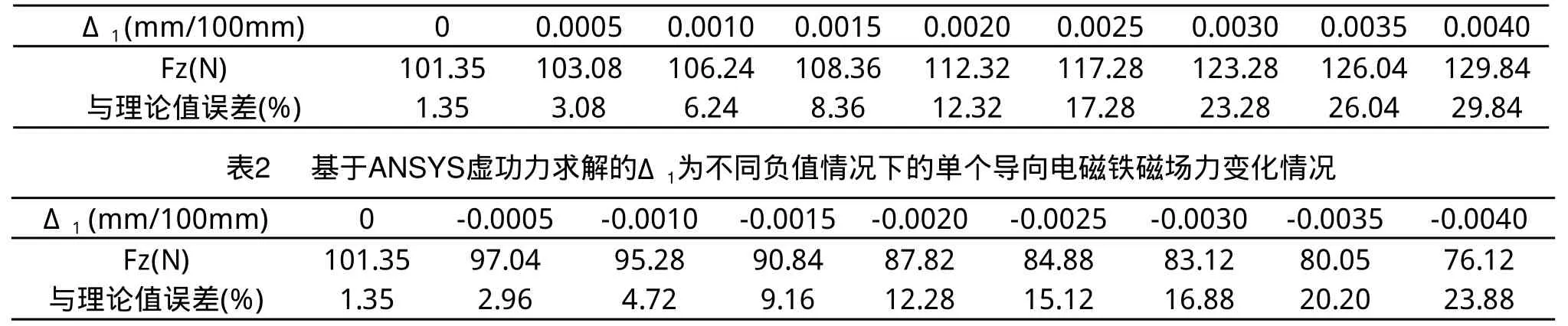
表1 基于ANSYS虛功力求解的Δ1為不同正值情況下的單個導向電磁鐵磁場力變化情況

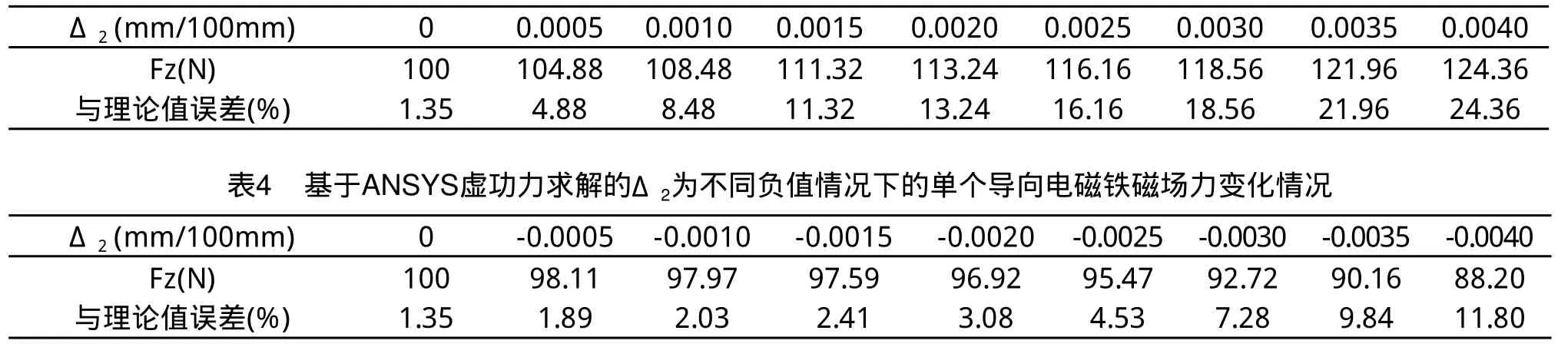
表3 基于ANSYS虛功力求解的Δ2為不同正值情況下的單個導向電磁鐵磁場力變化情況

由表3、4可知，當Δ2值為正時，導向電磁鐵與導向導軌之間的實際懸浮氣隙值小于理論設計值，所產生的實際電磁力將大于理論設計值100N，當Δ2值達到0.0010mm/100mm時，導向電磁鐵所生產的實際電磁力將急劇增大，與理論計算值的誤差超過了5%；當Δ2值為負時，導向電磁鐵與導向導軌之間的實際懸浮氣隙值大于理論設計值，所產生的實際電磁力將小于理論設計值100N，當Δ2值達到-0.0030mm/100mm時，導向電磁鐵所生產的實際電磁力將急劇減小，與理論計算值的誤差超過了5%。因此，導向電磁鐵在加工時，應將其在水平平面內的直線度控制在-0.0025~0.0005mm/100mm內。

由上述分析可知，導向導軌在水平面和垂直面內的直線度的正、負偏差均對導向電磁力產生較大影響，尤其是直線度正偏差對導向電磁力的影響，這是因為當N、S等參數確定時，導向磁場力僅與δ2的倒數成正比（如公式(1)所示），兩者的關系如圖8所示。

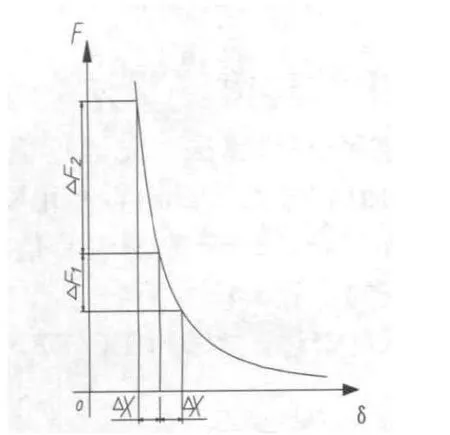
圖8 導向電磁力F與懸浮氣隙δ的函數關系圖

由圖8可知，懸浮氣隙增大ΔX所引起的導向電磁力的減小量ΔF1小于減小ΔX所引起的導向電磁力的增大量ΔF2，因此，導向導軌在加工時，其直線度負偏差要求要高于正偏差要求。

3 結論

通過對磁懸浮機床導軌直線度對導向磁場力的影響分析計算，可得出以下結論：

1）采用ANSYS有限元分析軟件對實例進行仿真與分析，得出了磁懸浮機床導軌中導向導軌分別在垂直和水平平面內直線度分別對導向電磁力的影響，為確定磁懸浮機床導軌的結構設計提供了理論依據。

2）導向導軌的直線度是影響導向電磁鐵與導向導軌之間懸浮氣隙不均勻的重要因素。導向導軌直線度正偏差對導向電磁鐵磁場力的影響大于負偏差對導向電磁鐵磁場力的影響。

3）文中，導向電磁鐵的最大磁場力為1 0 0N，當導向導軌在水平和垂直平面內的直線度分別控制在-0.0010~0.0005mm/100mm和-0.0025~0.0005mm/100mm之內時，滿足工作要求。

[1] 李朝國.機床導軌精度測量方法探討[J].金屬加工(冷加工),2011,(24):51-53.

[2] 鐘洋,陶衛軍,韓軍.滾柱直線導軌副精度損失模型及其試驗研究[J].組合機床與自動化加工技術,2013, (1):14-17.

[3] 廖萍,馬蘇揚,吳國慶,等.磁懸浮機床導軌電磁場分析[J].機床與液壓,2010,38(23):25-28.

[4] Li Qunm ing,Gao Dan,Deng Hua, et a.l.Modal Analysis of a High-precision Magnetic Suspension Stage[C] Proceedings o f the 7th Wo rld Cong ress on Intelligen t Con tro l and Au tom ation.Chongqing,2008.6:6044-6048.

[5] 郭磊.磁懸浮平臺承載特性研究.[D].長沙:中南大學,2005.

[6] 陳衛兵,茅靖峰.磁懸浮系統的變速趨近律滑模控制[J].制造業自動化,2010,32(6):80-83.

[7] 葉正環.導軌導向精度對加工精度的影響[J].太原師范學院學報(自然科學版),2007,6(1):67-70.

[8] 閻照文,等.Ansys10.0工程電磁分析技術與實例詳解[M].北京:中國水利水電出版社,2006.