多重柔性下輪式懸架移動機械手載體驅動力分析
孫凌宇,彭 平,王媛媛,李 蕊
(河北工業大學 機械工程學院,天津 300130)
0 引言
輪式懸架移動機械手系統是由一個機械手固定在一個全方位輪式懸架移動平臺上構成。其多重柔性是指由輪式懸架移動平臺構成的彈性阻尼柔性系統和多自由度機械手柔性系統。與剛性機械手相比,柔性機械手具有質量輕、體積小、速度高、能耗小、成本低等優點。國內外學者對柔性移動機械手的動力學[1~8]及控制[9~13]方面研究較多,對柔性移動機械手的載體驅動力較少進行探討。由于彈性阻尼懸架和機械手各構件柔性的引入,輪式懸架移動載體的驅動力是一個與各構件的彈性變量相關的復雜函數。本文綜合考慮了機械手桿件的彈性變形、移動載體的線彈性-阻尼懸架和不平路面等工況,分析計算了輪式懸架移動柔性機械手載體驅力學模型。
1 系統描述與計算
1.1 系統描述
如圖1所示,輪式懸架移動載體經過不平整地面時,移動載體坐標系產生的傾角,桿件與整體坐標系夾角為定義為移動載體——構件1(i=1),桿件坐標系原點相對于整體坐標系原點的位置矢量。

圖1 多重柔性下輪式懸架移動機械手
基于歐拉-伯努力梁單元理論[14,15],采用有限元法[14]將桿件2、3、4均離散為3個單元,如圖2所示。
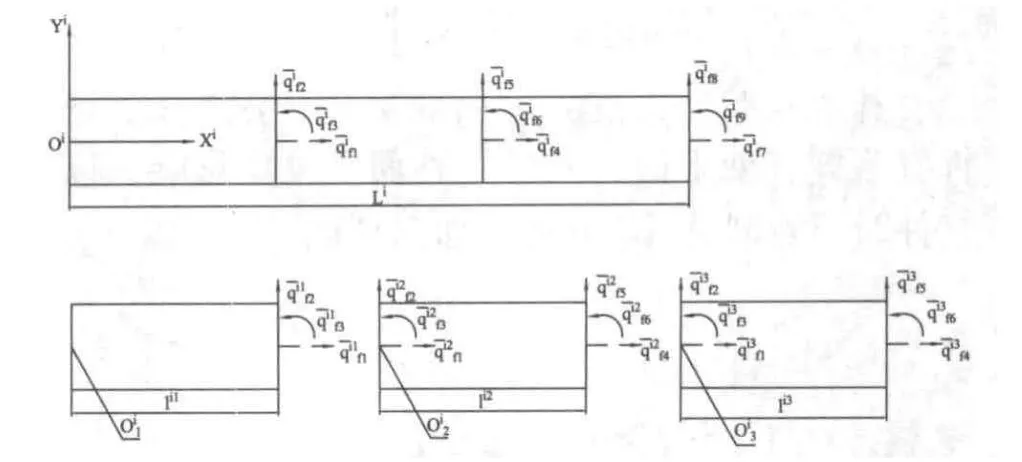
圖2 桿件i有限元離散(i=2、3、4)
桿件2上任一點相對于整體坐標系 的位置矢量為:
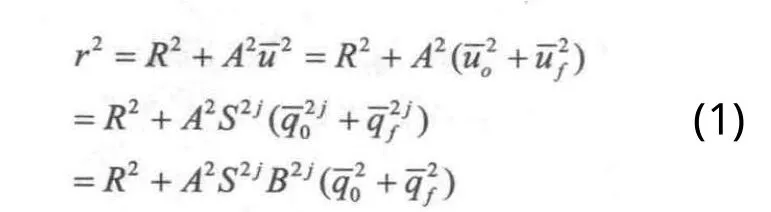
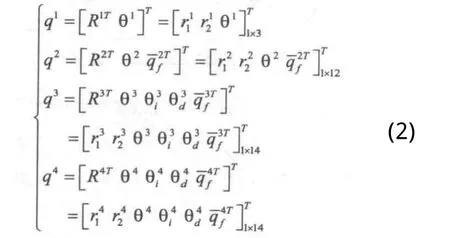
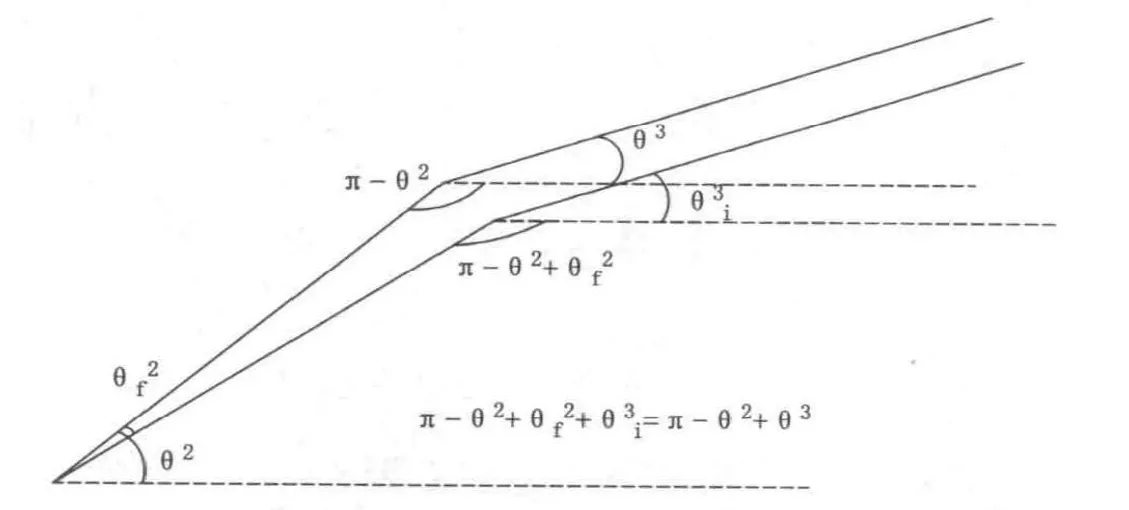
圖3 柔性機械手相鄰桿件彈性變形影響
移動機械手運動約束方程

1.2 獨立坐標變量與關聯坐標變量分離
系統中的廣義坐標變量可分為獨立坐標變量與關聯坐標變量。其中,獨立坐標變量各量彼此線性獨立,是系統坐標變量發生變化的主動因素,而關聯坐標變量則可由獨立坐標變量表示。按照這個原理,由約束方程(3)進行獨立坐標變量與關聯坐標變量分離:。其中為系統獨立坐標變量,為系統關聯坐標變量, 如下定義:
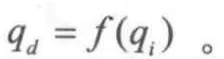
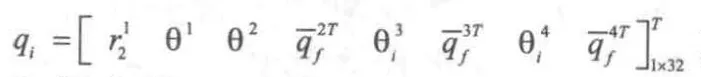


則可用系統獨立坐標變量表示該輪式懸架移動柔性機械手構型:
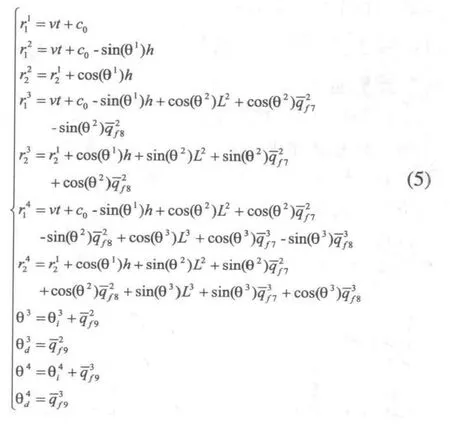
1.3 質量矩陣求解
根據公式(1) ,在整體坐標系下,桿件2上j單元上任意一點的速度可表示為:
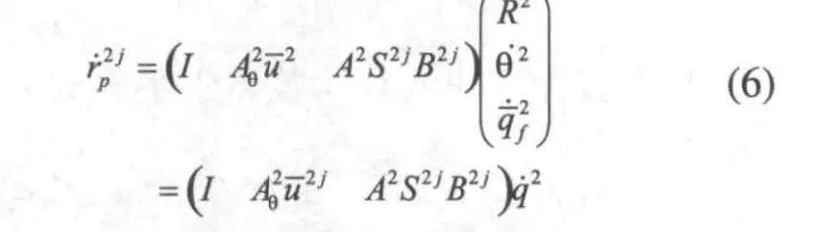
則桿件2的單元j動能為:
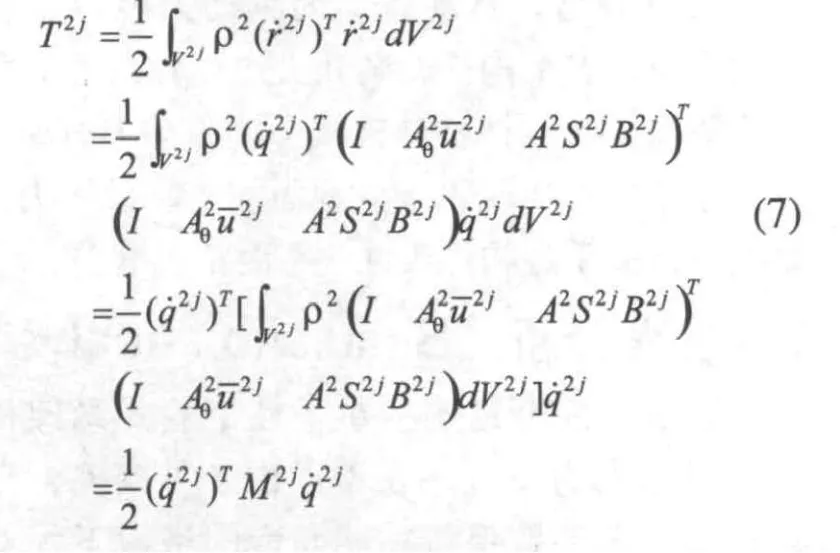
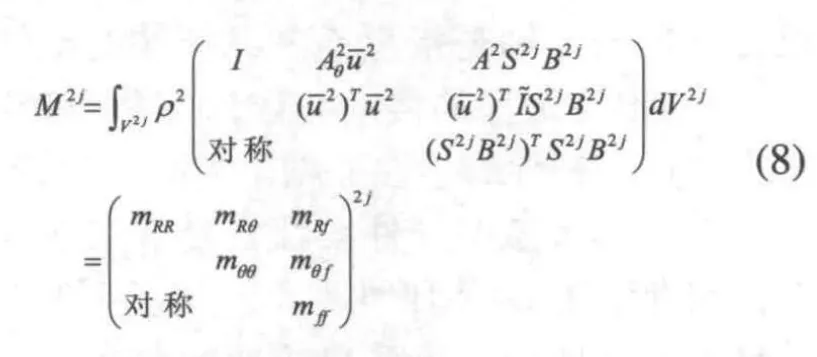
桿件2的動能和質量矩陣為:
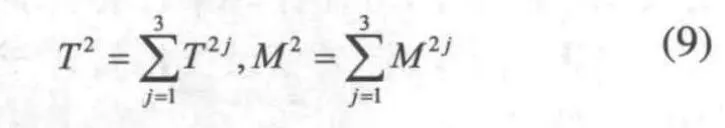

1.4 系統廣義力分析與推導
如圖1所示,路面用正弦函數可描述為:

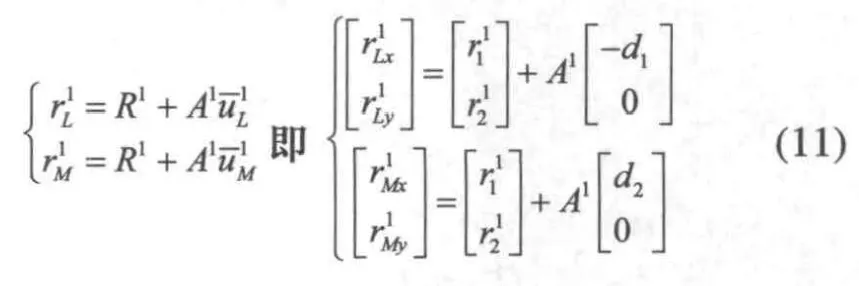
簡化有:

則有:
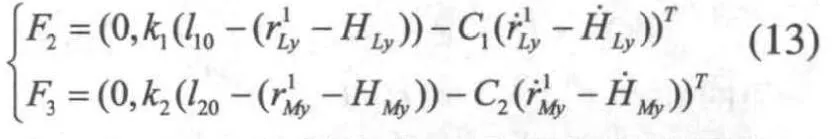
如圖4所示,分別對構件1,桿件2、3、4進行受力分析。其中、、分別是相應關節電機的扭矩,是移動載體在運動過程中受到的滾動摩擦力,分別是構件1、桿件2、3、4所受重力,為末端執行器受到的外力,這些都屬于外力。、、、、、是相鄰桿件間作用力,屬內力。其中:
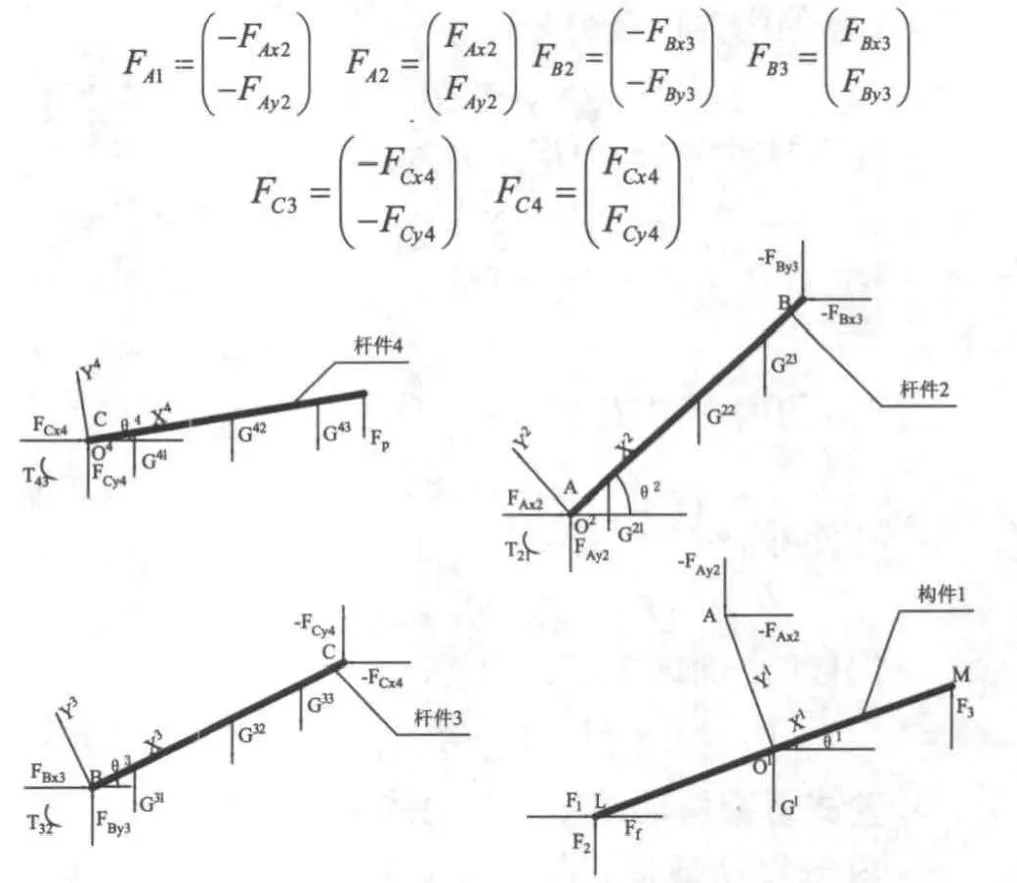
圖4 多重柔性下輪式懸架移動機械手各構件受力分析
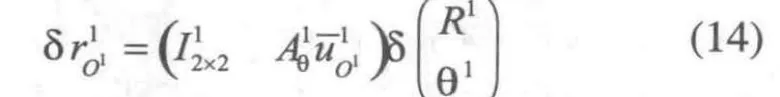
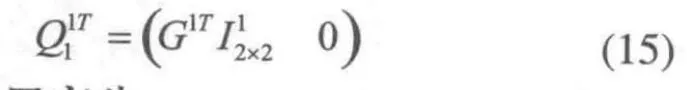
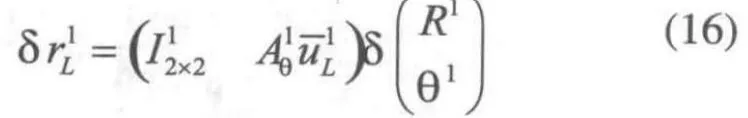


則構件1的外力廣義力為:
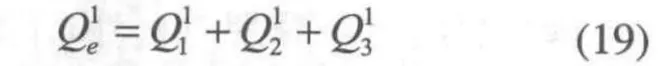

同理可得桿件2的外力廣義力為:



同理桿件3的外力廣義力為:



桿件4的外力廣義力為:
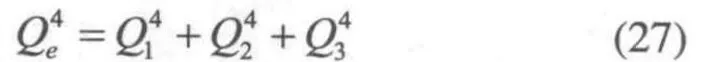
同理C點的內力廣義力為:

1.5 輪式懸架移動載體驅動力的求解
針對構件1和桿件2、3、4,其牛頓-歐拉方程為:
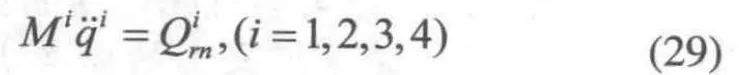
其中:
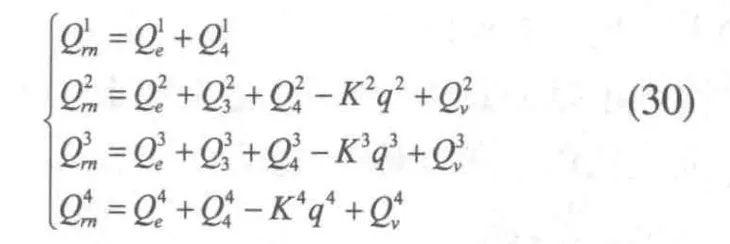
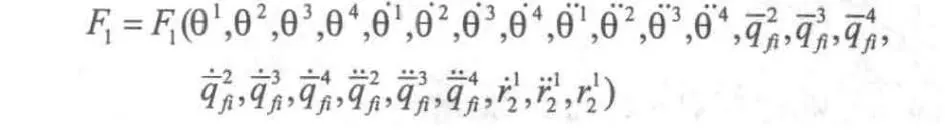
可以看出,移動載體的驅動力包含了桿件的彈性變量,各個構件的轉角。柔性輪式懸架移動機械手驅動力與剛性移動機械手的驅動力有所不同,它并不是單純克服輪子與地面間的靜摩擦力,還與系統中機械手各構件柔性、路面狀況有關。
2 仿真分析(Simulation analysis)
以本文的介紹的多重柔性下輪式懸架移動機械手機器人為模型,在不考慮各種摩擦、車體勻速運動、各手臂保持初始角度的情況下,對其進行剛性和柔性的末端執行器位置仿真和載體驅動力仿真,仿真結果如圖5、圖6所示。剛性情況與柔性情況的區別是指考不考慮桿件的柔性。從圖5可以看出,路面的波動導致末端執行器在y方向產生波動,桿件的柔性加劇了末端執行器在y方向的振動,如果忽略桿件柔性將降低末端執行器的定位精度。圖6表示剛性和柔性情況下的載體驅動力情況,從圖中可以看出柔性的存在引起驅動力的波動,如果忽略桿件的柔性將降低控制的精確度。兩圖的表達與實際情況相符,驗證了本文模型的合理性。
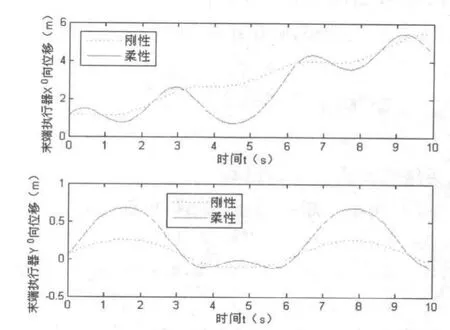
圖5 末端執行器位置仿真
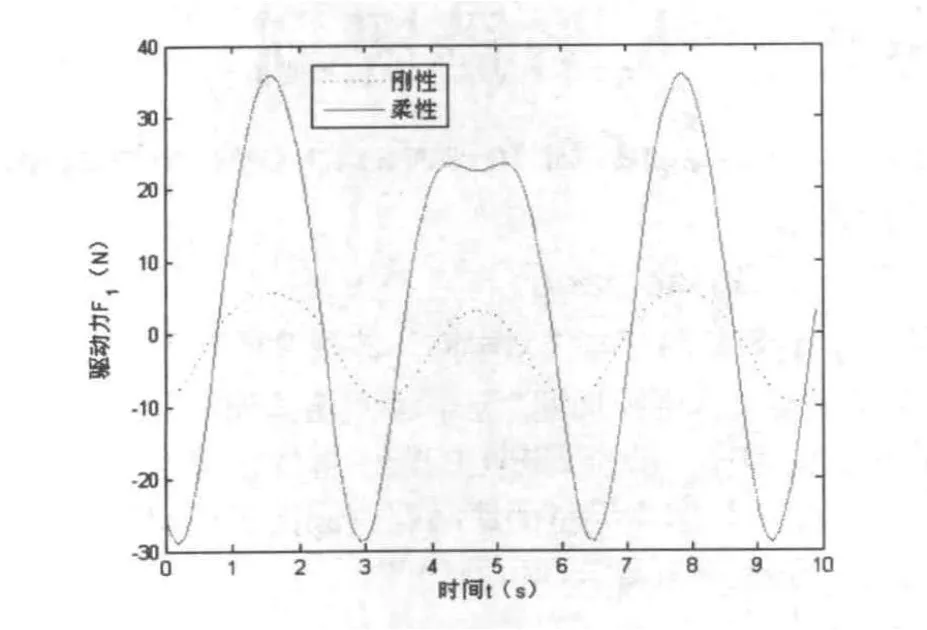
圖6 載體驅動力仿真
3 結論
本文以多重柔性下輪式懸架移動機械手為研究對象,首次提取了系統獨立坐標變量和關聯坐標變量,使系統構型表達更加簡潔,以此為基礎做系統動力學分析,可有效減少方程數目;在分析輪式懸架移動柔性機械手的質量矩陣和系統廣義力的基礎上,計算出包含柔性機械手各構件彈性變量的輪式懸架移動載體的驅動力模型。最后進行仿真分析,驗證了模型的合理性,并且表明如果忽略桿件柔性將降低末端執行器的定位精度和整體系統的控制精度。本文載體驅動力模型可作為該輪式懸架移動機械手系統的控制工作的基礎和參考。
[1] Mete Kalyoncu.Mathem atical m odelling and dynam ic response o f a m u lti-straigh t-line path tracing flexib le robot m anipulator w ith rotating-p rismatic joint[J].App lied Mathem atical Modelling, 2008,32(6):1087-1098.
[2] Akira Abe.Trajecto ry p lanning for residual vib ration supp ression o f a tw o-link rigid-flexib le m anipu lator considering large deform ation[J].Mechanism and Machine Theory, 2009,44(9):1627-1639.
[3] And ré Fenili,José Manoel Balthazar. The rigid-flexib le nonlinear robotic m anipulator: Modeling and control [J].Comm unications in Nonlinear Science and Numerical Sim u lation,2011,16(5):2332-2341.
[4] Barun Pratiher,San tosha Kum ar Dw ivedy. Non-linear dynam ics of a flexib le sing le link Cartesian m anipu lator[J].International Journal of Non-Linear Mechanics, 2007,42(9):1062-1073.
[5] Hassan Zohoor,Sayyid Mahd i Khorsand ijou. Dynam ic m odel o f a flying m anipu lator w ith tw o high ly flexib le links[J].App lied Mathem atical Modelling,2008,32(10):2117-2132.
[6] 章定國.多桿空間柔性機器人遞推Lag range動力學建模和仿真[J].應用數學和力學,2009,30(10):1202-1212.
[7] 今天,王樹新,丁杰男.計及環境特征的柔性多體系統動力學理論[J].機械工程學報,2005,41(5): 26-30.
[8] 胡權,賈英宏,徐世杰.多體系統動力學Kane方法的改進[J].力學學報,2011,43(5):968-972.
[9] M.S. Alam, M.O.Tokhi. Hyb rid fuzzy logic con tro l w ith genetic op tim isation for a single-link flexible manipulator[J]. Engineering App lications o f Artificial In telligence,2008,21(6):858-873.
[10] B. Subudhi, A.S. Morris. Soft computing methods applied to the contro l of a flexib le robot m anipulator[J].App lied So ft Com pu ting,2009,9(1):149-158.
[11] M.Z. Md Zain,M.O.Tokhi,Z.Moham ed. Hybrid learning con tro l schem es w ith inpu t shap ing o f a flexib le m anip u lato r system[J].Mechatronics,2006,16(3-4):209-219.
[12] Ali Tavasoli,Mohamm ad Eghtesad, Hamed Jafarian.Tw o-tim e scale control and observer design for trajectory tracking of tw o cooperating robot m anipulators m oving a flexible beam[J].Robotics and Autonomous System s,2009,57(2):212-221.
[13] Marco Sabatini,Paolo Gasbarri, Riccardo Monti, et al.Vibration control of a flexib le space m anipulator during on orbit operations[J].Acta Astronautica,2012,73(4-5):109-121.
[14] 陸佑方.柔性多體系統動力學[M].北京:高等教育出版社,1996.
[15] 楊玉維,張明路,崔峰.4自由度輪式懸架移動機械手動力學研究與仿真[J].機械設計,2009,26(4): 35-41.
[16] Bian Yushu,Gao Zhihui,Yun Chao.Vibration Reduction o f Open-chain Flexib le Manipu lators by Op tim izing Independent Motions of Branch Links[J].Chinese Journal o f Aeronautics,2008,21(1):79-85.

