含間隙機構神經網絡建模及其智能控制
李庭貴,薛邵文
(1.瀘州職業技術學院,瀘州 646005;2.四川省瀘州市工程機械智能優化設計重點實驗室,瀘州 646005)
0 引言
間隙的存在使副元素在運動過程中發生碰撞分離,從而引起機構的劇烈震動,降低了系統的穩定性和精度,尤其在高速機構的設計中,這種影響更大。因此,在機構的分析和設計過程中,必須考慮間隙對系統的影響。而對于如何比較準確的建立含間隙機構動力學模型進行仿真實驗是至關重要的,國內外許多研究學者在這方面進行了大量的研究工作[1~6]。由于很難確定機構在分離和接觸兩種狀態過渡時的各項運動參數,故很難建立比較精確的數學模型。為了解決這個問題,采用神經網絡(Neural Network,NN)對含間隙機構建模,它以其特有的學習能力和逼近函數的功能,使其可以對任何非線性系統進行建模。為了減輕或消除機構運動副間隙所引起的不穩定性,國內外很多學者從不同的控制方法入手開展了研究工作[7,8],但僅僅處于初步探索階段,只是從理論上用一些被動控制的方法研究了間隙的控制問題,但研究對象為單桿的簡單機構,或是從優化設計[9,10]的角度出發,利用優化算法重新分配機構的結構參數,該方法雖然在一定程度上控制了間隙的不良反應,但是其改變了機構原有的組成參數,故有可能惡化機構的其它動態特性。本文針對含間隙連桿機構,采用BP神經網絡離線對含間隙連桿機構進行建模,并對其建立逆模型;利用神經網絡超強的魯棒性和模糊控制的人性化與智能化,對含間隙連桿機構間隙產生的誤差分別進行了神經網絡內模控制和參數自調整模糊控制研究實驗,取得了比較滿意的控制結果。
1 建模
1.1 連桿機構實驗系統
由于含間隙連桿機構是一個強非線性系統,系統建模非常復雜,很難建立比較準確的數學模型。因此,在建模時通過所測試數據,采用BP神經網絡離線對含間隙連桿機構建模。通過連桿機構實驗系統(The Experimental System of Linkage Mechanism)獲得測試實際數據,其工作原理為利用連桿機構作往復運動的滑塊(Slider Crank)推動光電脈沖編碼器(Photoelectric Pulse Encoder),通過同步脈沖發生器(Synchronous Pulse Generator)輸出與滑塊位移相當的脈沖信號,然后輸入到機械動態參數測試儀(Mechanical Dynam ic Parameter Tester),再經過微處理器進行數據處理,輸出測試數據。
通過試驗,測得連桿機構理想情況下與含間隙時滑塊位移對比數據如圖1所示。
由圖1可知,由于間隙的存在,使得系統很不穩定,連桿機構位移誤差如圖2所示,在2rad和4rad以及8rad左右的時候,誤差比較大,偏差大概在4mm左右,尤其在不到5rad時位移誤差達到了負向最大,達到4.5mm左右,對于這種不穩定的系統在系統運行中缺乏可靠性。所以,為了減少或者消除這種誤差給系統帶來的不穩定性,本文采用圖3和圖4所示的控制模型,對位移誤差進行消除。
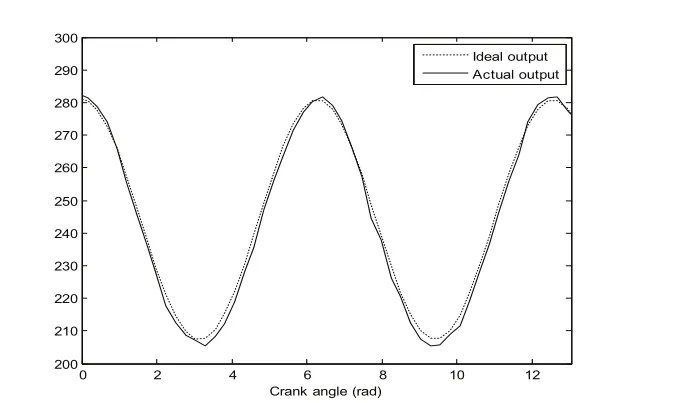
圖1 連桿機構位移示意圖
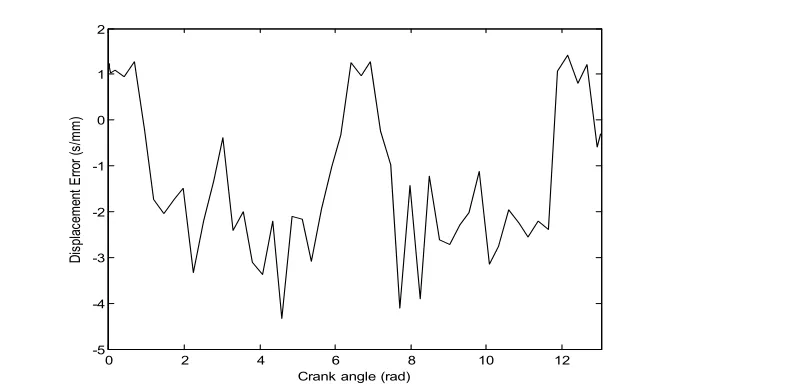
圖2 連桿機構位移誤差示意圖
1.2 含間隙連桿機構建模
采用神經網絡構造含間隙連桿機構的模型。其辨識結構采用串并聯的形式,P為系統被控對象,即連桿機構,P-1(NN)是學習被控對象的神經網絡模型。由被控對象P的輸入u(k)和輸出z(k)作為P-1(NN)神經網絡的輸入,通過網絡訓練不斷調整權值,不斷地減小P-1(NN)網絡模型輸出和被控對象P輸出z(k)的差值e(k),最終達到P-1(NN)對被控對象的模擬。
采用離散型非線性差分方程來描述被控對象P,如公式(1)所示。
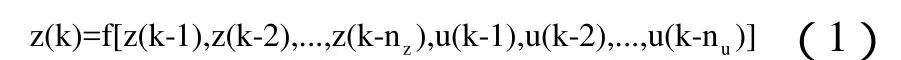
式中:f(·)是未知非線性函數;nz是輸出的階次,nu是輸入的階次。此式說明在k時刻的輸出,取決于過去nz個時刻的輸出值以及過去nu個時刻的輸入值。
在系統建模時,被控對象的采集樣本集由若干組歷史數據{u(k),z(k)}組成,對采集數據進行歸一化處理,使u(k)∈[0,1],z(k)由實測的位移信號映射到區間[0,1]。
下面采用BP神經網絡進行控制,選用三層網絡:有1個輸入節點、6個隱層節點、1個輸出節點,隱含層采用Tansig函數,輸出層采用Purelin函數作為它們的傳遞函數。其輸出可用公式(2)-(4)計算。
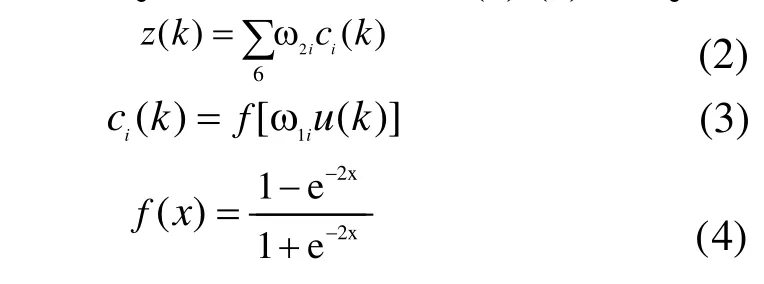
式中:z(k)和u(k)分別為網絡輸出、輸入;ci(k)為隱含層各節點輸出;1iω為輸入層到隱含層的連接權值;2iω為隱含層到輸出層的連接權值。
為了評價BP神經網絡的學習狀況,用被控對象輸出和網絡模型輸出的誤差平方和(取L2范數)為目標函數:
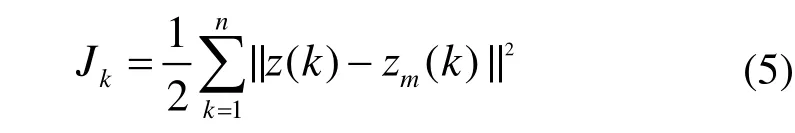
式中:n為樣本組數,zm(k)為被控對象輸出,學習目標是使Jk≤σ,σ為預先設定的一個很小的值。
在BP神經網絡中,誤差信號從后向前傳遞,在反向傳播的過程中,逐層修改連接權值。由(5)式中的Jk計算在誤差信號的反向傳播過程中各層連接權值的調整,使網絡的輸出接近期望的輸出。
1)輸入層M上任一節點與隱含層I上任一節點之間連接權值調整為
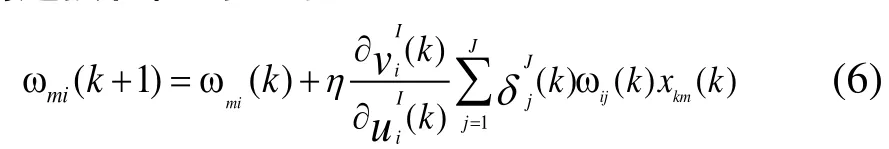
式中:η為學習因子,在本系統建模中取0.1。
2)隱含層I上任一節點與輸出層P上任一節點的連接權值調整為
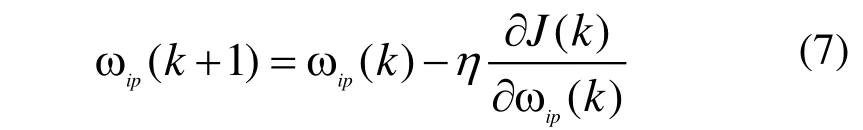
BP神經網絡各層間權值的初始值在實際建模中,是隨機給定的,采用BP算法訓練網絡,訓練200次左右即可使訓練目標誤差小于0.001。
1.3 含間隙連桿機構逆模型
從系統求逆理論和高等數學可知,系統正模型和逆模型的關系可被認為是映射和逆映射的關系。把被控對象的逆狀態NN-1模型與被控對象NN串聯,那么,NN-1輸入就等于被控對象NN的輸出,即
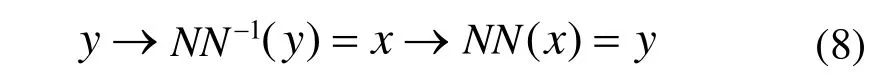
模型的具體建立過程與其正模型基本一致,只是將輸入和輸出調換即可,所不同的是逆模型中,BP神經網絡有4個隱層節點。
2 補償控制
含間隙系統是一個強非線性系統,系統及其外部環境具有很多未知和不確定的模糊性因素,采用經典控制理論和現代控制理論無法得到滿意的控制效果。神經網絡以生物神經網絡為模擬基礎,使人工智能更接近人腦的自組織和并行處理等功能,具有逼近任意非線性函數的能力,以及并行分布計算、自學習和容錯能力。模糊控制是以模糊邏輯為基礎,抓住人類思維中模糊性的特點,模仿人的思維方式,對復雜的非線性、時變系統實施控制,具有魯棒性強,以語言變量代替常規的數學變量等特點。下面分別采用神經網絡內模控制和參數自調整模糊控制對系統誤差進行控制。
2.1 神經網絡內模控制
采用神經網絡內模控制模型[11]來控制含間隙連桿機構的誤差。基于NN的內模控制結構如圖3所示。
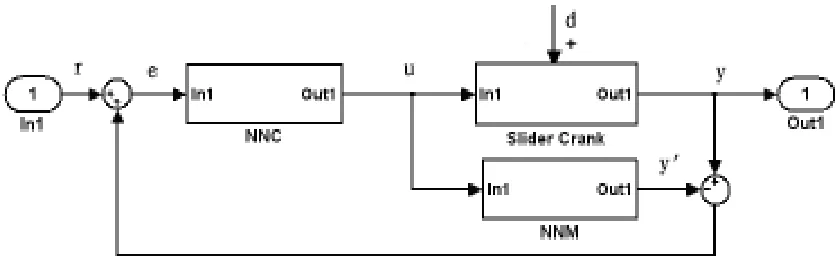
圖3 神經網絡內模控制
在NN內模控制結構中,采用神經網絡模型(NNM)來模擬系統的特性,用模型的逆模型即NN-1作為NNC,附加外部隨機干擾信號d到Slider Crank系統,將對象與模型的誤差 f = y - y '反饋到參考輸入r,構成閉環系統。如果神經網絡模型(NNM)能夠準確的表達對象Slider Crank的輸入輸出關系,反饋信號f=0,系統為開環(y = r),是直接逆控制。若由于模型不準確以及干擾等原因,y≠ y',則由于負反饋的作用,仍可使y接近r。
神經網絡內模控制系統誤差如圖5所示。分析比較圖2和圖3可以明顯看到,采用神經網絡內模控制,使系統誤差減小,并且誤差穩定在一定的區間范圍,最大位移誤差從4mm左右減小到2.7mm,使系統控制精度大大提高。因此,神經網絡內模控制具有很強的魯棒性,是一種較好的控制方案。
2.2 參數自調整模糊控制
采用參數自調整模糊控制來控制含間隙連桿機構的誤差。模糊控制器采用M am dani算法,輸入為滑塊位移的偏差E和偏差變化率EC,輸出為曲柄速度V,描述輸入/控制量的語言值模糊子集選取為:{NB,NS,ZO,PS,PB},其中:NB=負大;NS=負小;ZO=零;PS=正小;PB=正大。
對n維輸入狀態xl,x2,…,xn,根據模糊控制規則“Rm:if xl isand x2 is…and xn isthen Um is Bm”,那么,第i條規則模糊輸出隸屬度為:
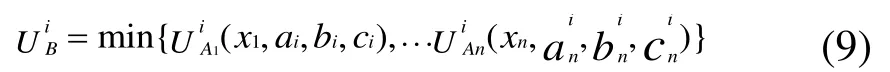
以重心法解模糊,則模糊系統的輸入、輸出關系為:
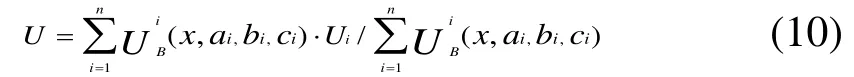
由上式可見,模糊控制器的輸出U由隸屬函數的參數ai、bi、ci和輸入狀態x1、x2、…、xn共同決定,因后者是由外部環境所決定,故模糊控制器的輸出主要取決于隸屬函數。
含間隙連桿機構的隸屬函數選用三角函數trim f,滑塊位移的隸屬函數取值范圍取-2~2;滑塊位移變化率的隸屬函數取值范圍取-100~100;曲柄速度的隸屬函數取值范圍取8.5~8.9。再根據給出的隸屬函數編出模糊規則,建立模糊控制器。
常規模糊控制器的量化因子 Ke、 Kec和比例因子 Ku是固定不變的,不能很好地滿足系統的靜態和動態性能要求,難以保證被控過程的全過程都處于最佳控制狀態。因此,采用參數自調整模糊控制[12]方式,根據誤差和誤差變化率的大小,控制器自動選取不同的參數值,在線調整 Ke、 Kec、Ku,以滿足系統的性能要求。參數自調整模糊控制系統結構如圖4所示,圖中的“Param eter Regulation System”模塊,通過“If-else”選擇語句編程來實現參數 Ke、 Kec、 Ku自調整。
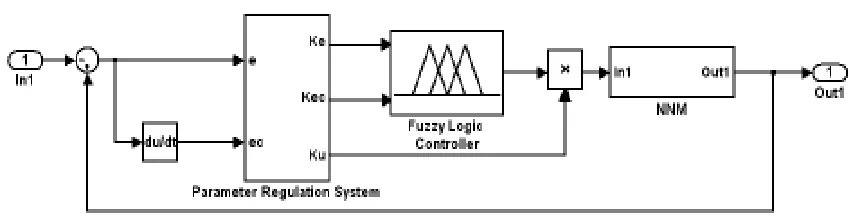
圖4 參數自調整FUZZY控制系統
參數自調整模糊控制系統誤差如圖5所示。仿真結果表明,采用參數自調整模糊控制,進一步提高了系統的穩定性和控制精度,最大位移誤差從2.7mm減小到1mm以下。
3 結論
本文提出了采用神經網絡對含間隙連桿機構建立模型和其逆模型的方法,并對含間隙連桿機構間隙產生的誤差進行了兩種非線性控制研究。通過圖2與圖5比較得知,采用神經網絡內模控制,系統最大誤差從4mm左右減小到2.7mm;采用參數自調整模糊控制,最大位移輸出誤差減小到1mm以下,控制精度有明顯的提高。實驗結果表明,采用神經網絡內模控制、參數自調整模糊控制來控制含間隙連桿機構系統誤差,控制效果明顯。
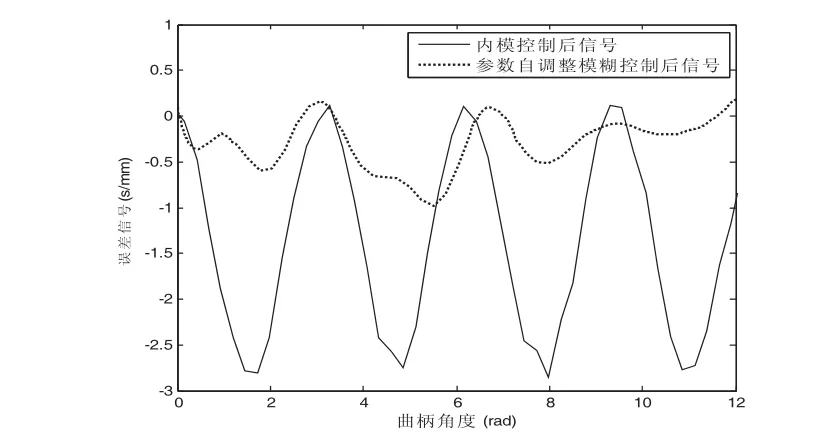
圖5 神經網絡內模控制和參數自調整模糊控制誤差對比圖
[1] Dubowsky S,Gardner T N.Dynamic interactions o f link elasticity and clearance connections in p lanarm echanical system s[J].Journal o f Engineering for Industry,1975,97B(2):652-661.J.Clerk Maxwell,A Treatise on Electricity and Magnetism,3rd ed.,Oxford:Clarendon,18 9(2):68–73.
[2] Earles SW E, Wu C L S. Motion analysis of a rigid - link mechanism w ith clearance at a bearing, using lagrangian mechanism and digital computation[R].Conference onMec hanisms,IME,London,England,1972:83—89.
[3] Seneviratne L D, Earles SW E.Chaotic Behaviour Exhibited During Contact Loss in a Clearance Joint of a Four-bar Mechanism [J]. Mechanism and Machine Theory,1992, 27(3):307—321.
[4] Mansour W M,Townsend M A.Im pact Spectra and Intensities for High-speed Mechanisms [J].Trans.ASME Journal of Engineering for Industry,1975,97B(2):347-353.
[5] Li Z,Li L,Bai S X. A New method of predicting the occurrence of contact loss between pairing elements in plannar linkages w ithclearance[J].Mech. Mach.Theory,1992,27(3):295-301.
[6] 王國慶,劉宏昭,何長安.含間隙連桿機構非線性行為研究[J].機械設計,2005,22(3):12-13.
[7] Tzou H S.Dynamic evaluation and passive control of design to tolerance between machine elements,In:Tipins V A,Patton E M.Computers in Engineering 1988,New York:ASME,1988.585-591.
[8] Ashwath N,Paul F W.Com puter control compensation for mechanical clearance in hyd rau lic robot joint servom echanism s,In : Paul F W,Youcef2 toum i K.Robo tic s:Theory and Appications,N ew York:ASME,1986.129-134.
[9] Feng Bin,Morita,Nobuyoshi,Torii,Takao.Optimization o f joint force on planar linkage,Transactions o f the Japan Society o f Mechanical Engineers,Part C,1995,61:2725-2729.
[10] 李哲.考慮運動副間隙和構件彈性的平面連桿機構動力學研究[D].北京:北京工業大學,1991.
[11] 叢爽.神經網絡、模糊系統及其在運動控制中的應用[M].合肥:中國科技大學出版社,2001.
[12] 孫增圻,等.智能控制理論與技術[M].北京:清華大學出版社,2003.

