基于超立方路徑規劃的發動機再制造物流作業調度策略

高 健，龍 偉，田大慶，李炎炎

（四川大學 制造科學與工程學院，成都 610065）

0 引言

航空發動機再制造不同于傳統的航空發動機生產制造，其具有多品種，小批量等特點，尤其對于發動機主件和附件的再制造，其工藝工序的多樣性程度和復雜程度十分突出，這與傳統的剛性離散制造系統依據輸入/輸出來作決策有著本質的區別。當我們把眾多型號發動機的傳統生產方式轉化為規模化可重構的制造模式時，這就要求其生產組織形態必須適應經常變化的作業過程。目前，面向系統的可重構研究主要集中在以機器為模塊進行制造系統的重構[1]。

自動導航車(Automated Guided Vehicles,AGV)是一種自動化的無人駕駛的智能化搬運設備,屬于移動式機器人系統,能夠沿預先設定的路徑行駛,是現代計算機集成制造系統中的關鍵設備之一[2]。可重構制造系統就是利用AGV的循跡特點進行生產組織形態的重組，從而使得航空發動機再制造車間能夠適應經常變化的加工流程。目前這方面研究集中在AGV本身技術以及AGV作業規劃調度方面。

對于復雜再制造系統，其車間作業調度路徑的拓撲結構可以有多種選擇，其算法主要解決的是AGV小車從起點到目標點的路徑問題[3]，主要有狀態空間法[4]、神經網絡法[5]、柵格法[6,7]、免疫網絡算法[8]、粒子群算法[9]和遺傳算法[10]等。

但是，現有的拓撲規劃理論和調度策略普遍存在著難以解決多目標，多約束，很少涉及實時調度，依賴輸入/輸出進行決策等問題：因此，研究探索能夠快速響應生產形態變化和過程決策傳導的作業規劃調度理論是航空發動機再制造系統實現可重構的重點和難點。

1 基于超立方路徑規劃的新方法

1.1 超立方的概念

本文提出的超立方路徑規劃思想，源于數學物理上的“超立方體”概念[11]，超立方體描述方法是尋找一個聚類的最小外接立方體，使其包含數據集中所有的數據點[12]。我們從超立方體中抽取一個胞粒作為基本立方體，如圖1（a）所示，由于它的八個角點可以通過多條路徑相連，于是可將每個角點都規為一個加工工位、倉儲貨架等。當需要并行協同加工工位或倉儲貨架之間的作業流程時，我們可按一定的規則來定義連接在立方體上的角點。

圖1 在物流作業路徑中引入超立方概念

設兩個相鄰角點的連接為一個鏈接語句，并以“面”為基本單元，如圖1（a）中 0-1-2-3 的上平面和 4-5-6-7 的下平面。如果把一個鏈接語句，定義成兩個角點連接的“鏈接閥”，則一個基面四個角點的兩兩互連，可用圖1（b）的鏈接展開圖來表示。同時，第一平面的每一個角點都可以與第二平面的任一角點相連且每一種鏈接方式都有唯一展開圖與之對應。如用圖1（a）所示的角點3和角點 4 之間的連線，將立方體上下兩基面連接起來，我們便可得到一種如圖2所示的立方體角點鏈接展開圖。

圖2 單胞粒上下基面角點的連接路徑

1.2 鏈接算法的簡單介紹

現規定：

設定一 設鏈接語句函數式為 link(x，y)，x為起始角點值，y為終止角點值，它們的三位二進制表達式為：

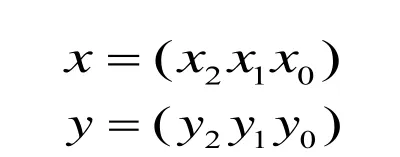
設定二 設 Box(i，j)為超立方角點鏈接閥，它的狀態對應于鏈接語句link(x，y)的“位”狀態值，并定義：

當 Box(i，j)＝0 時，則表示i與i直鏈，或j與j直鏈；

當 Box(i，j)＝1時，則表示i與j交鏈，或j與i交鏈；

于是，link(x，y) 的位狀態可表示為：

例如，當角點 0與角點1的鏈接，其 link(0,1)＝[10]，則有：

可見，Box(0,1)＝1，表示角點0與角點1交鏈；Box(0,1)＝0，表示角點0與角點1直鏈。

設定三 設鏈接語句的運算規則為二進制的“位加”運算，即兩個二進制同位相加后取其個位的值，并用運算符“”來表示。根據定義，我們對圖2中上虛框所表示的第一基面角點的鏈接算法推導如下：

1）相同角點的直鏈語句：

2）不同角點的直鏈語句：

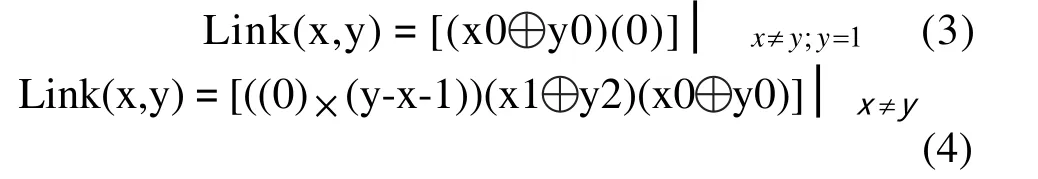
例如：

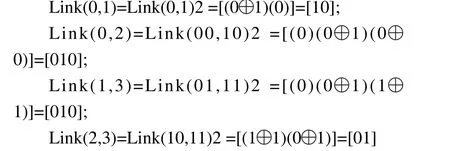
3）間隔角點的鏈接語句：

由于不同角點的直鏈語句具有可逆性，因而可以用它來生成間隔角點的鏈接狀態，即把相鄰角點的首尾狀態值連接后消去，可用“⊙”表示。通常，間隔角點的鏈接具有多條路徑可以選擇，如：

4）交叉角點的鏈接語句：

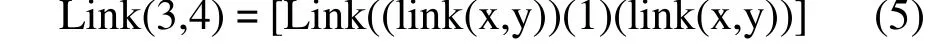
對于圖2中下虛框所表示的第二基面角點的鏈接算法，只需將角點值減去(k-1)×4 后（k 為立方體的基面數），套用上平面的鏈接算法，然后將上下兩個基面的鏈接值帶入交叉鏈接語句即可。其他基面也照此類推。

1.3 引入估價函數

由上述算法介紹得知，兩角點之間時常存在多條鏈接路徑，因此存在路徑最優問題，選擇的依據通常有時間因素，距離因素，擁堵因素以及直角拐點因素等[13]，為方便起見，本文只引入距離估價函數以取得最優解。引入笛卡爾坐標系，保存每個角點的坐標值。估價函數形式：

上述算法，我們把它定義為“基于超立方模型的路徑鏈接算法”。

2 調度流程

如圖3所示，根據車間實際情況設置節點布置位置，并提取節點笛卡爾坐標值，設置不連通路徑，當AGV小車接受任務時應先根據任務的起始和終止點求出兩節點分別所在基面，以便得出鏈接路徑中共有多少交叉角點鏈接。

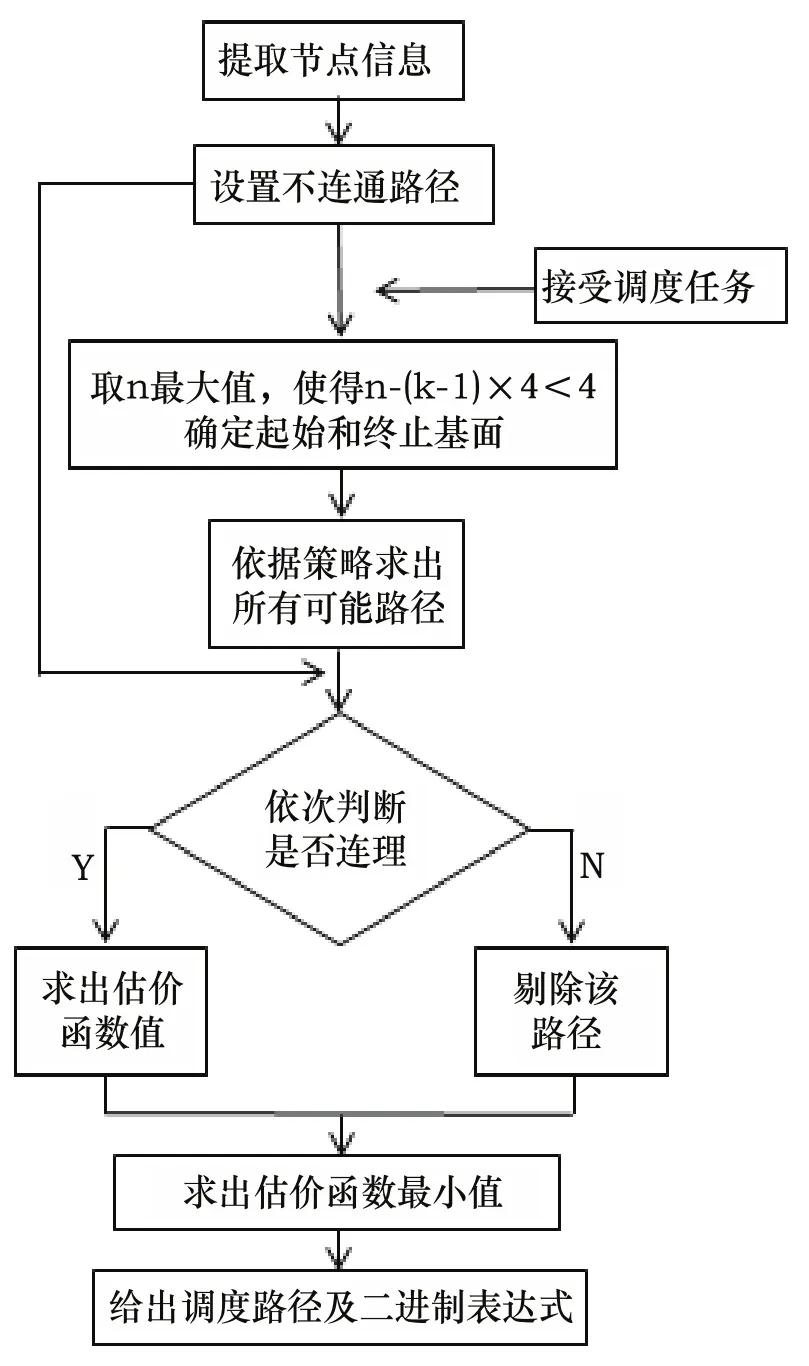
圖3 調度流程

根據調度算法求出的路徑不一定都符合車間的實際情況，此時就需要剔除原先設定的不連通路徑。每一條符合要求的路徑均由若干節點組成，每依次相鄰節點間均有一估價函數值，而這條路徑的估價函數值是所有節點函數值的總和，最優路徑就是依據最小估價函數值來選擇。

3 調度算法模型與物理形態的轉換

我們可進一步將圖2所示的鏈接規則，轉換為相應的制造物流作業路徑連接的物理形態，為方便可行，我們將工位 2 與工位 3 的位置互換，將工位 6 與工位 7 的位置互換，圖 4就是采用交鏈語句來連接上下兩個基面的多工位路徑鏈接的物理形態示意圖。

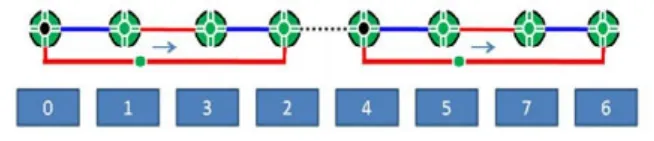
圖4 超立方路徑的物理結構

對于多基面問題，我們只需要在圖4的基礎上加以順延即可，如圖5所示。

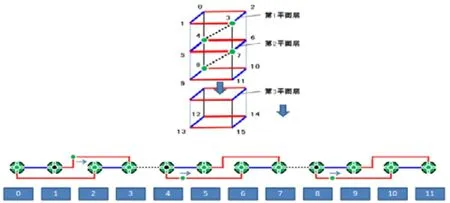
圖5 多重超立方路徑的物理結構

在此基礎上，根據航空發動機再制造車間特點，本文給出了車間布局的示意圖，如圖6所示。

圖6 航空發動機再制造車間布局示意圖

4 算例

例如某一航空發動機再制造車間布局如圖7所示。其中0-3節點為航空發動機主體再制造單元，4-11節點為物料配送中心入倉口，12-18節點為航空發動機控制器再制造區，現物流小車調度任務為從貨架3上取一零件送至工位11處。

具體處理方法如下：

1）提取每個角點坐標信息，如表1所示，根據車間實際擺放情況，設定第一基面和第二基面之間只有0和4以及2和6可通，在同一基面內各節點都可通；

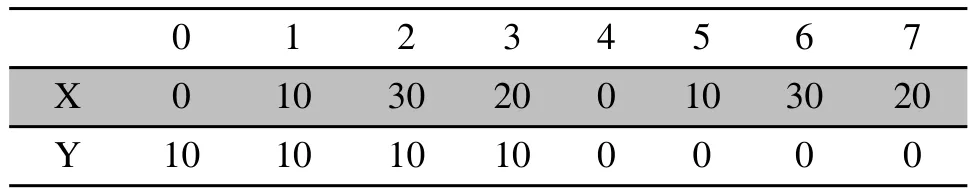
表1 各角點笛卡爾坐標

2）對于起始角點3，求的K=1，即在第一基面，終止角點4，求的K=2，即在第二基面；

3）起始角點和終止角點不在同一基面，且其中含有一個交叉角點鏈接；

4）剔除步驟1中設定的不連通路徑，根據超立方理論模型，共得出6種鏈接路徑，如表2所示；

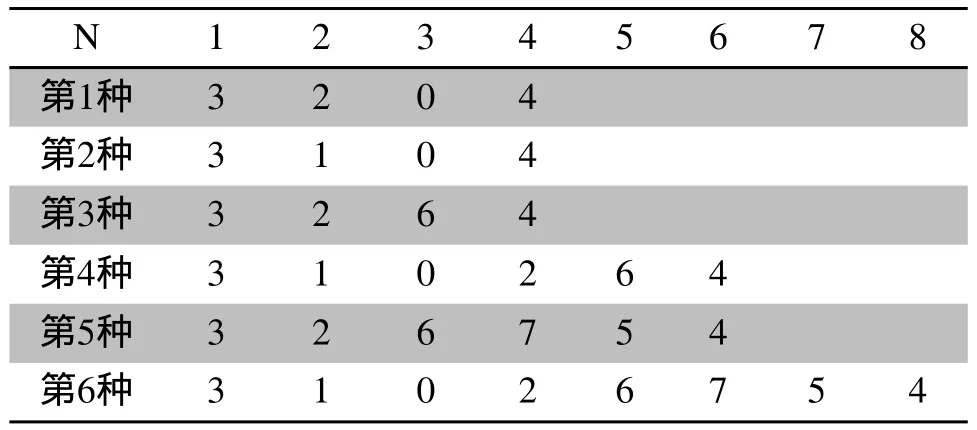
表2 枚舉鏈接路徑

5）利用估價函數，求的每種路徑的函數值如表3所示；

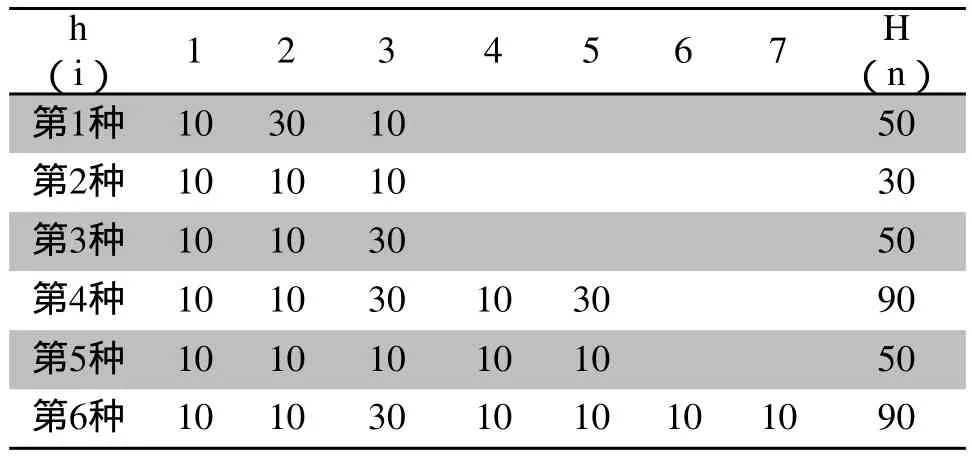
表3 估計函數值

6）由表3得最優路徑為第2種，其二進制表述為：

其中：

link(3,4)=link[link(3,0) (1)]

link(3,0)=link(3,1)⊙link(1,0)=[0101]

所以link(3,4)=[01011]。

5 結論

盡管人們在互聯網絡、神經網絡、集成電路、通信技術等領域，對超立方體拓撲結構及路徑理論進行了大量研究，但本質上大都側重在超立方體的全域“聚類點基元”的大規模并行處理的理論技術局面，需要進行復雜的數學運算處理。本文研究，通過“面基元”來構造與可重構制造物流模態相對應的“網格結構”，并提出了“超立方路徑的鏈接算法”，為航空發動機再制造車間的作業過程提供了實時調度，傳導敏化的新方法，本算法避免了全域搜索所帶來的計算量大的問題，利用人為設置路徑通斷，既進一步增強了系統的可重構性也強調了過程決策，但是更加普適，通用的超立方理論及其傳導模態還需要進一步研究。

[1] 王曉勇,臧鐵鋼,陳富林.制造系統可重構控制技術研究[J].制造業自動化,2007,11(29):23-27.

[2] 徐清.自動導引小車系統的設計與實現[D].蘇州:蘇州大學,2006.

[3] 孫奇.AGV系統路徑規劃技術研究[D].浙江,浙江大學,2012.

[4] 胡正興,李一民,詹躍東.自動導引小車局部智能避障的A*算法[J].昆明理工大學學報,2005,30(5):51.

[5] 肖本賢,齊東流,劉海霞,等.動態環境中基于模糊神經網絡的AGV路徑規劃[J].系統仿真學報,2006,18(9):2401.

[6] 鄧高峰,張雪萍,劉彥萍.一種障礙環境下機器人路徑規劃的蟻群粒子群算法[J].控制理論與應用,2009,26(s),879-883.

[7] 李天成,孫樹棟,高揚.基于扇形柵格地圖的移動機器人全局路徑規劃[J].機器人,2010,32(4),547-552.

[8] 方慶館,黃建中.基于環境地圖的AGV路徑規劃免疫網絡算法研究[J].起重運輸機械,2010,20(3):42-4.

[9] 邊培瑩,李德信,包寶軍,路燕.粒子群算法在生產物流調度中的應用研[J].計算機工程與應用,2010,46(17):220-223.

[10] ZHAN Y u-dong,LUO Y ing.The goods-f low ing system AGV technology of Yuxi cigarette factory and the developmental research of AGV nationalization technology[C]∥IEEE International Vehicle Electronics Conference. Piscataway:IEEE Press,1999:425-428.

[11] 林崔琴,超立方圖和超立方有向圖的同構因子分解[J].清華大學學報(自然科學版),1992,32(3):24-29.

[12] 劉英帆,崔江濤.基于聯合聚類的超立方體高維索引[J].計算機科學與探索,2012,06(00).

[13] 賀麗娜.AGV 系統運行路徑優化技術研究[D].南京,南京航空航天大學,2012.