雙通道角跟蹤設備的近場相位校準研究

習 靖

(中國電子科技集團公司第五十四研究所，河北石家莊 050081)

0 引言

目前航天測控系統中的自跟蹤通常采用差模跟蹤［1］體制，利用差模電場方向圖在天線軸線方向為零，在偏離軸線方向上具有極性非零值來實現跟蹤。在上述跟蹤系統中，跟蹤接收機和差通道的相位差必須控制在一定的范圍內才能保證跟蹤的穩定性，測控設備執行任務前需要對和差通道相位差進行標校與調整(以下簡稱校相)。隨著天線口徑的加大和工作頻段的提高，校相所需要的遠場［2］條件越來越難以滿足，導致設備在對塔校相后對塔跟蹤性能良好，對衛星跟蹤后系統定向靈敏度及交叉耦合系數變差，從而引起系統跟蹤不穩定的問題［3］。針對該問題研究了多模饋源、雙通道單脈沖跟蹤系統天線和、差口對源天線輻射場的近場響應［4］，得出由于天線感應電壓引入的附加相位差和標校距離的關系曲線，并給出了不同工作頻段的雙通道單脈沖跟蹤設備相位校準修正值。為解決設備近場標校問題提供相關技術參考。

1 自跟蹤原理及數學模型

航天測控系統的自跟蹤設備一般采用連續波信號體制，它利用多模饋源對飛行器輻射信號所激勵和模信號的單峰特性和激勵差模信號的雙峰特性來實現對飛行器目標的自動跟蹤［5－7］。

假定測控天線(跟蹤天線)電軸偏離飛行目標一個小角度θ，并且θ在跟蹤天線直角坐標平面內與天線方位軸的夾角為β。那么信標信號在饋源內激勵的和模與差模信號可以分別表示為:

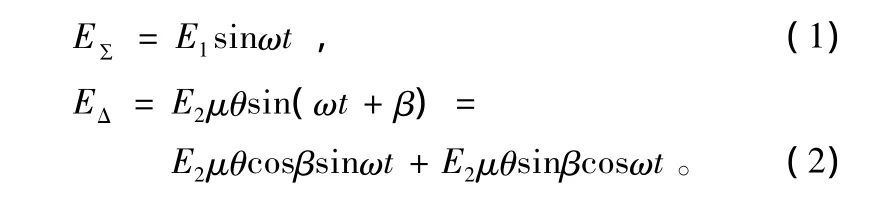
式中，μ為天線差斜率(設定為常數);ω為信標信號角頻率;t為時間變量;E1為和模信號幅度;E2為差模信號幅度。

顯然，式(2)中θcosβ和θsinβ就是天線電軸偏離目標θ角在天線直角座標系方位軸A和俯仰軸E上產生的角誤差信息。也就是說天線偏離目標所產生的差模信號EΔ中既包含了偏離目標的方位角度信息，又包含了偏離目標的俯仰角度信息。角誤差信號示意圖如圖1所示。

圖1 角誤差信號示意

天線多模饋源激勵的和模與差模信號EΣ和EΔ被分別饋入跟蹤接收機的和、差信道，進行放大、變頻和A/D變換;其中EΣ信號經過數字中頻接收機跟蹤濾波，產生2路正交的I、Q信號:

而另一路數字化后的差信號，被和信號進行幅度歸一化和相位歸一化處理后，表示為:

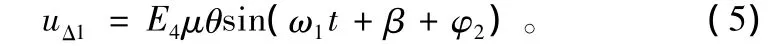
式中，ω1為ω變頻后的信號角頻率;E3為與E1相應的信號幅度;E4為與E2相應的信號幅度;φ1為和信道設備引起的信號相移;φ2為差信道設備引起的信號相移。

角誤差信號的解調過程可表示為:

2路解調信號分別經過低通濾波后，輸出方位、俯仰角誤差信號的HT表達式為:

式中，E5=1/2E3E4。

從式(8)和式(9)可以看出:ΔuA中含有 ΔuE的信號分量，ΔuE中含有ΔuA的信號分量。這2個信號分量稱交叉耦合信號。經過自跟蹤設備的標校后，使表達式中的φ1與φ2的差值為零時，就可以獲得真實的角誤差信號為:

將角誤差信號ΔuA和ΔuE饋入伺服設備，驅動天線朝著角誤差信號減少的方向運動，直至ΔuA、ΔuE為零，就實現了天線對目標的自跟蹤。

2 天線近場響應

2.1 接收天線對源天線的近場響應

在三維系統中，一般可以利用Robieux定理，通過計算復數傳輸系數來確定2個天線間的耦合關系，并依此研究一個天線對另外一個天線輻射場的響應［8］。但因為坐標系比較復雜，所以定量研究源天線口徑的尺寸對響應的影響是困難的。

天線和、差口對近場源天線的響應由天線近場輻射場以及源天線口徑場點乘決定。但是要進行詳細計算非常麻煩，可以對其進行進一步簡化:假設源天線為各向同性的點源天線(工程應用中，一般采用波瓣寬度遠遠大于跟蹤天線的波瓣寬度的寬波束天線作源天線，完全可以做這種假設)，向四周輻射均等，其口徑特性不對接收天線構成影響。

有了以上假設后，天線對源天線輻射場的近場響應實際上就是其近場方向圖。

2.2 卡塞格倫天線的近似處理

卡塞格倫天線在航天測控系統中應用廣泛，計算卡氏天線的輻射場可以分別計算饋源、副反射面和主反射面的輻射場，但這種方法計算過于復雜，計算量太大，同時不適合用口徑場積分法計算。所謂的等效方法是先將卡氏天線等效為普通的拋物面天線，然后計算其輻射特性。傳統的等效方法分為等效饋源法和等效拋物面法。

等效饋源法是將饋源與副反射面組合成一個虛饋源并放置在主面焦點上;等效拋物面法是用一個口徑與主面相同的拋物面代替主、副反射面，饋源不變，改變的是焦距。與等效饋源法相比，等效拋物面法不改變饋源輻射場，等效拋物面天線和實際反射面天線的口徑場分布相同，沒有增大計算的復雜程度，因此本文采用該種方法等效。

等效后，卡塞格倫天線的和、差方向圖可表示為［9］:

Es(u)為天線和方向圖;ED(u)為天線差方向圖;aR為被測天線的口徑半徑;aH為饋電喇叭的口徑半徑;F為卡氏天線的等效焦距。

3 雙通道角跟蹤設備近場校相分析

3.1 和差通道相差的測量方法

對于采用數字基帶技術的中頻接收機來說，測量相位差比較容易，一般測控設備中有2種測量方法［10］:相位法和幅度法。

3.1.1 相位法

在數字接收機中，采集差通道的I、Q支路數據x(k)、y(k)，做數學運算φ =arctan，可求得和差通道相差與目標空間相位之和β+Δφ，在校相時，可根據天線實際空間位置，算得Δφ。

3.1.2 幅度法

在測角天線控制單元中，采集方位、俯仰誤差電壓數據ΔuA、ΔuE，做數學運算φ =arctan可求得和差通道相差與目標空間相位之和β+Δφ。同樣，可根據天線實際空間相對于天線方位俯仰軸的位置，算得Δφ。

3.2 天線近場感應引入和差信道相位差仿真分析

近場標校的情況下，接收天線和、差方向圖的相對相位較遠場發生變化，導致接收天線饋源和、差口對源天線輻射場的近場響應的相對相位發生變化，主要表現在近場條件下和、差口對來波信號的感應電壓之間的相位差使和差通道的相位差發生變化。天線對源天線輻射場的近場響應導致天線和、差口對來波信號的感應電壓之間出現附加相位差。對卡塞格倫天線的近場方向圖進行分析和仿真，研究天線近場和差方向圖的相對相位，得出了天線近場和差方向圖的相對相位差與距離的關系。

圖2是S頻段12 m天線工作頻率為2250 MHz的和差口相對相位差與距離的仿真曲線，圖中R為信標天線與標校天線的距離，R0=2D2/λ為滿足遠場條件的距離。

理想情況下，和差相位差為0°或180°，實際工程中用到的校相公式都是在理想情況下推導的。工程中由于實際條件的限制在任務前對設備校相時，一般都是在近場條件下進行的系統校相時，基帶設備的移相值包含了由于天線感應電壓引入的附加相位差，而跟蹤衛星時，附加相位差很小，導致近場校相后跟蹤真實目標時精度變差。

圖2 天線和差口相對相位差與距離的關系

通過研究天線的近場方向圖可以計算出天線近場條件下和差口相對相位差與距離的關系，這樣就可以得出和差通道實際的相位調整值和設備測出的相位調整值之間的關系，即

式中，Δφ真為設備實際應調整的和差通道相位差;Δφ測為設備測量的和差通道相位差;Δφ近場為近場耦合導致的和差通道相位差。

3.3 驗證

實際工程中對上述修正進行了驗證。天線距標校塔距離為726 m，為遠場距離的1/3左右。對比結果如表1所示。

表1 實際工程與仿真比對結果

通過表1可以看出，實際結果與工程結果相符，實際工程中，可以按照本文的方法對校相結果進行修正。

4 結束語

航天測控系統工程中由于不能滿足遠場條件，導致設備在對塔校相后對塔跟蹤性能良好，對衛星跟蹤后系統定向靈敏度及交叉耦合系數變差，從而引起系統跟蹤不穩定的問題。本文針對該問題，通過理論和仿真的方法，分析了近場校相時導致和差相位相移值不準的原因，并給出了S頻段相位修正曲線。對實際工程中解決近場標校問題提供相關技術參考。 ■

［1］趙業福.無線電跟蹤測量［M］.北京:國防工業出版社，2003:10－20.

［2］毛乃宏，俱新德.天線測量手冊［M］.北京:國防工業出版社，1987:1－30.

［3］毛南平，從 波，段慶光，等.近場效應對一種C頻段統一測控雷達角度標校數據的影響分析［J］.電訊技術，2008(4):65－68.

［4］JULL J V.An Investigation of Near-Field Radiation Patterns Measured with Large Antennas［J］.IRE Transactions on Antennas and Propogation，1962，AP-10(4):363－367.

［5］石 榮，陳錫明，唐 海，等.差模跟蹤接收機和差通道相位標校與調整 ［J］.電子信息對抗技術，2006(1):6－9.

［6］袁 剛，江 濤.差模跟蹤技術的應用［J］.現代雷達，2004(1):49－52.

［7］柯樹人.圓波導多模自跟蹤系統的工作原理［J］.通信與測控，1992(2):1－11.

［8］MILLIGAN T A.Modern Antenna Design(Second Edition)［M］.America:John Wiley ＆ Sons Inc.，2005:380－447.

［9］柯樹人.自跟蹤天線和、差口對源天線輻射場的近場響應［J］.通信與測控，1990(3):1－10.

［10］成亞勇，李玉瑄.雙通道角跟蹤體制實時校相算法研究［J］.無線電工程，2009，39(5):32－33.