太赫茲準光傳輸面臨的挑戰

李春化 魏志強 王元源

(西安電子工程研究所 西安 710100)

0 引言

太赫茲(TeraHertz)，簡寫為THz，1 Tera=1012，太赫茲頻段是指0.1THz～10THz 的頻率范圍。由于受大氣中的分子吸收的影響，大氣分子對太赫茲波有很強的衰減。在頻率位于0.5THz 以上，大氣分子對太赫茲波的衰減高達700dB/km［1］，如此強的衰減使得太赫茲波在地球大氣層中幾乎無法傳播，只有在含水量較低的太空，才有可能進行傳播。除了大氣衰減外，太赫茲在波導中傳輸也受到很大的限制。雖然有報道表明，太赫茲波可以通過光子晶體波導、介質波導和金屬波導傳輸，但采用波導傳輸會引起實際使用上的困難，不適合遠距離傳輸，這里的遠距離通常指大于幾十個波長的距離范圍。以金屬波導為例，太赫茲頻率高，波導尺寸小(對于1mm 波長，波導尺寸為0.8mm×0.4mm)，很難進行精確加工，即使能夠加工，對加工精度的要求也很高。當在波導內安裝一個二極管時，為了保證波阻抗和二極管低阻抗匹配，還需要降低波導高度，使得波導尺寸更小。當波導尺寸減小時，波導損耗會進一步增大。研究表明，在THz 波段，波導損耗約為0.3.～0.5dB/λ［2］，這里λ 是電磁波的波長。

為了解決波導傳輸帶來的損耗問題，人們試圖尋求其它的傳輸方式。使用自由空間替代波導傳輸太赫茲波就是一個有前景的傳輸方法，這種自由空間傳輸太赫茲波的方法稱為準光技術［3-5］。準光技術是在近幾十年在毫米波、亞毫米波研究過程中發展起來的基礎理論，它是光束傳播理論在毫米波段的自然擴展，然而應用準光技術仍由許多需要探討的問題。

本文第二部分在回顧準光理論的基礎上，從透鏡設計原理出發，討論光束傳播和準光傳播在理論上和實際應用上的異同。在第三部分對準光透鏡設計中實際遇到的設計問題進行討論。在本文第四部分，對需要進一步研究的準光課題和傅里葉光學在準光系統中應用問題提出個人見解。作者希望通過對這些問題的思考，起到拋磚引玉的作用，也歡迎同行批評指正。

1 準光傳輸技術—自由空間傳輸

研究表明，當電磁波的頻率超過75GHz 時，波導傳輸損耗很大，使用自由空間作為傳輸介質代替波導傳輸太赫茲波成為一種有吸引力的傳輸方法［1］。這種類似光束傳輸的方式被稱為準光(quasi-optics)傳輸技術。在電磁波自由空間中傳輸時，電磁波將向自由空間的任何方向傳播，因此必須通過透鏡、反射鏡等各種器件限制或改變電磁波的傳輸范圍和傳輸方向［2］，且在自由空間中電磁波有多種極化方式，因此，準光技術需要研究各種透鏡、透鏡組合以及各種極化器的實現原理。這種使用透鏡、反射鏡等原理構成的傳輸系統，稱為波束波導系統［2］。準光傳輸不同于光的傳輸，需要建立適合于太赫茲波的透鏡設計方法和計算方法。

1.1 準光系統中的光線理論

使用透鏡傳輸光線已為大家所熟知，在長達上百年的發展歷史中，已經建立起來成熟的透鏡設計方法和透鏡系統的分析方法，比如光線光學就是將光的傳播看成一條光線而建立起來的幾何光學方法，而光學矩陣是建立在幾何光學基礎之上的一個簡單有效的光學分析方法。人們自然要問，能否使用光線光學來分析準光系統，如果能夠將光線光學直接移植到準光系統中，人們就不需要“重新發明一個輪子”。

為了回答這個問題，需要研究光線光學中的基本假設條件。在光線光學中，之所以能夠將光的傳輸看成光線，是因為透鏡的尺寸遠大于光的波長。舉例來說，可見光的波長λ～0.5μm，如果透鏡直徑D=25mm，D/λ=50000，光學透鏡的大小比波長大5萬倍，而且光線光學中要求波束橫截面至少比波長大2 個數量級，即100 倍。能夠將光的傳播看成光線的必要條件是D/λ 足夠大，光的衍射效應可以忽略。如果在太赫茲波系統中，也建立同樣的比例關系，將透鏡的尺寸按照與光波長類比的方式等比例放大到幾萬倍的話，那么可以將光線理論直接應用到太赫茲系統中。例如，如果THz 的波長為1mm，我們要求波束直徑大于100mm，而且透鏡尺寸為50000 ×1mm=50m。在實際中是不可能建造如此大的透鏡系統。在THz 波段，我們希望透鏡的尺寸只有幾倍的波長，而不是上萬倍。在這個限制條件下，THz 波段衍射效應無法忽略。因而，光線光學不能適應太赫茲系統，而必須尋求新的理論基礎。人們尋求透鏡尺寸只有幾個波長的光學設計方法，這個方法叫做準光設計方法。

下面以一個實際的透鏡天線的例子說明透鏡參數與波長的關系，文獻［7］設計了一個工作在35GHz 的透鏡天線，它的設計參數見表1。

表1 3GHz 透鏡天線設計參數

從表1 可以看出，透鏡的直徑Dλ是波長的66倍，而非上萬倍，焦點大小dλ是波長的0.48 倍，而非100 倍。正是由于這些參數與波長的比值遠小于光學波段相應參數與光波長的比值，才使得準光處理不同于光學處理。

1.2 高斯波束

光線光學不再適用太赫茲波，而高斯波束被認為是很適合用來描述太赫茲波的傳播。高斯波束是下面的Helmholtz 方程在近軸近似條件下的近似解［2］

其中，Ψ 是電磁場的分布;k=2π/λ 是波數;λ 為波長。其近似條件是場分布，Ψ 的大部分能量集中在傳播軸附近，且在z 軸的傳播方向上，Ψ 的幅度是慢變化過程。忽略Ψ 的z 方向二階導數，方程的解為:

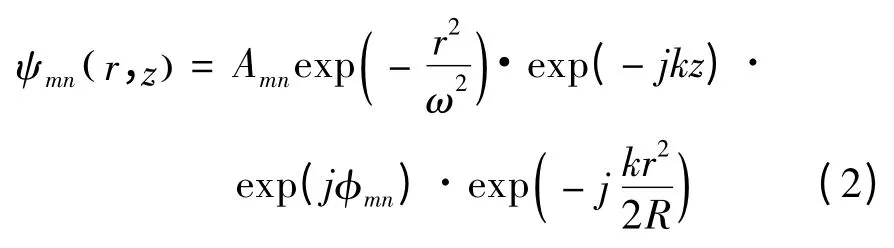
其中Amn是波束歸一化常數，可視為Amn=1;r=是距離波束軸的距離;z 是波束距離束腰的距離。高斯波束具有高次模，因此(2)式中ψmn(r，z)是mn 模的場分布，定義波束束腰位于z=0，束腰大小是ω，高斯波束的場分布的橫截面如圖1 所示，各個參數的意義也在圖1 中給出。

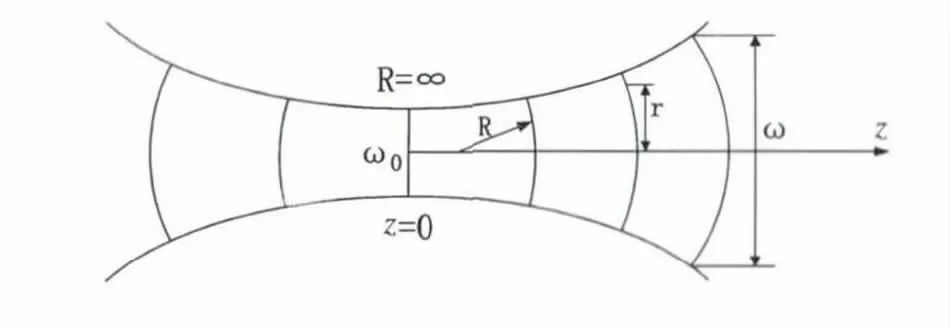
圖1 高斯波束截面和參數定義

(2)式中，等號右側各項物理意義分別是高斯輪廓、平面波相位、附加相位和球面波相位。第一個指數項表示高斯波束的幅度大小是高斯分布，在波束軸上強度最大，遠離波束軸，幅度按照高斯分布減小。第二項表示平面波傳播距離z 處，引起的相位滯后。第三項為高斯波束的附加相位項φmn，其大小與模數m，n 有關。第四項是球面波的相位，各參數之間的關系如下:

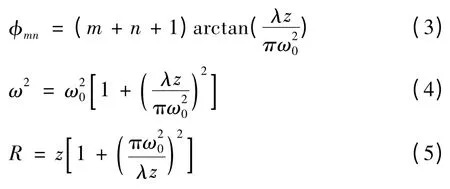
球面波的場分布，如式(6)所示。比較(2)和(6)兩式可發現，除了幅度因子外，高斯波束相對于球面波多了一個相位因子φmn，它是波面傳播距離z的函數，正是該附加相位因子使得高斯波束不同于球面波。

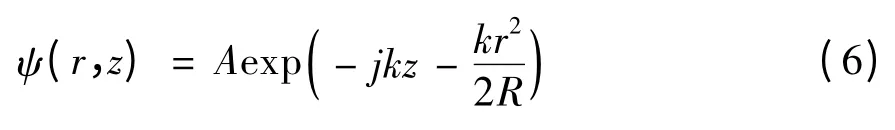
在光線光學中，假定能量沿波前的法向傳播，相位波前是球面的。在任何垂直波前的表面上，功率可以看成是從一個點源發出的發散波，或者向一個點源匯聚的匯聚波。而在式(2)中，波前的曲率半徑R與距離z 有關，雖然高斯波束可以看成是點源發射的球面波，但這個點源的位置不是固定在波束軸上，而是沿波束軸移動，因此高斯波束不是同心的球面波。由于這些差異，導致光學透鏡設計方法不同于高斯波束透鏡設計方法。

1.3 光學透鏡與準光透鏡的區別

為了了解它們的不同之處，考慮一個球面波波束入射到一個光學薄透鏡時的情景，如圖2 所示。我們可以從透鏡的焦點畫一系列的同心圓直達透鏡表面，根據Snell 定理和透鏡的聚焦特性來決定折射光線的方向，從而確定透鏡表面方程。

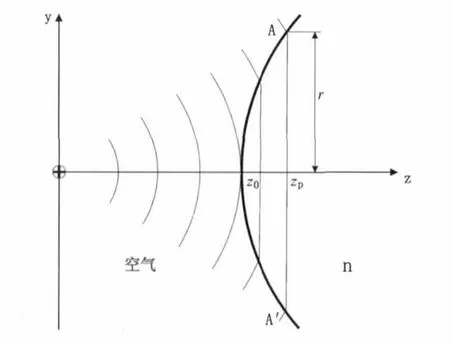
圖2 光學透鏡對球面波的聚焦

假設z 軸為波束軸，一個點源位于z=0 平面，透鏡垂直于波束軸放置于點源的右邊，透鏡的頂點位于z=z0平面。當波在z ＜z0范圍內傳播時，波在空氣介質中傳播，波前是球面波。當波進入透鏡時，由于透鏡的主要作用是對波前的曲率進行修正，使得在透鏡內部，波前按照平面波傳播。因此在z=zp平面，光軸上點的波束相位由兩部分組成，一部分是波在空氣中從z=0 傳播到z=z0時的相位-kz0，另一部分是波進入透鏡后，在介電常數為n 的介質中傳播時相位-kn(zp-z0)，這兩部分之和構成總的相位α1。

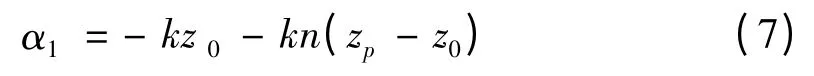
式中，n 是透鏡材料的介電常數。在遠離光軸r 處的A 點，波束在到達A 點之前按照球面波傳播，在A 點的波束相位為:

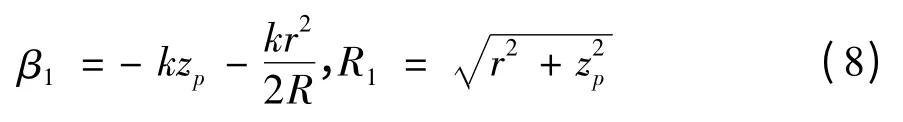
如果要求光束在透鏡內的波前是平面波，則上面兩式相等，將r 和zp聯系起來，透鏡表面將滿足方程:

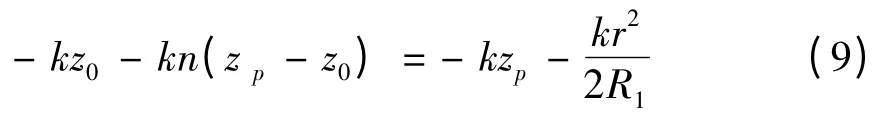
而對于高斯波束來說，建立如圖3 所示的坐標系統，假定波束束腰位于z=0 平面，波沿z 軸正向傳播。在z=zp平面，光軸上點的波束相位也由兩部分組成，一部分是波從z=0 傳播到z=z0高斯波束引起的相位-kz0+φmn(z0)，另一部分是波進入透鏡后的平面波相位-kn(zp-z0)，這兩部分構成總的光程，其相位α2為:

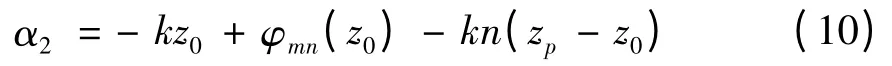
在距離光軸r 處的A 點，波束在達到A 點之前按照高斯束傳播，其相位β2為:

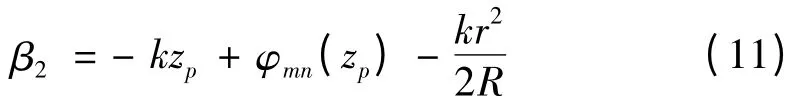
同樣為了滿足光束在透鏡內的波前是平面波的要求，要求在z=zp平面上，軸上的波前和軸外的波前是等相位的，因而令α2與β2相等，可得:

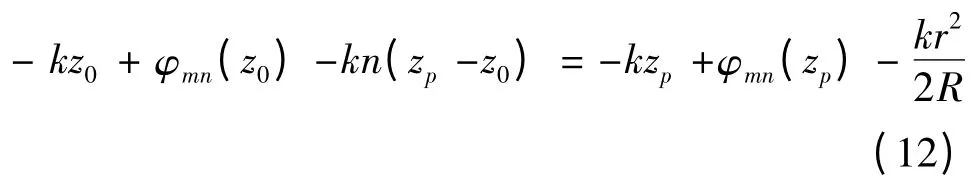
上式將透鏡參數r 和zp聯系起來，給出了傳輸高斯波束時，透鏡表面所必須滿足的方程。

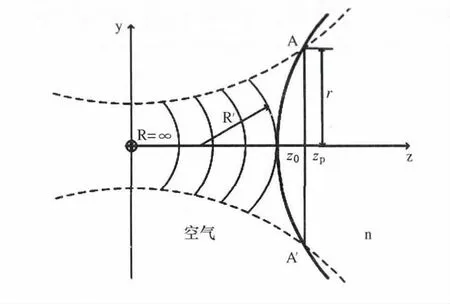
圖3 準光透鏡對高斯波束的聚焦

比較式(9)和式(12)可以看出，由于高斯波束特征，光學透鏡和準光透鏡所需要滿足的方程式不同的，不能直接應用光學透鏡設計方法來設計準光透鏡。由于高斯波束傳播時附加相位φmn(z)的存在，使得高斯波束不能按照光線來處理。雖然高斯波束的波前可以看成是球面波，但高斯球面波的球心不是在同一點，而是沿z 軸移動。基于這些特點，高斯波束不能看成是從同一點源發出的光線，也就不能把它看成光線。如果說光學是基于光線的理論，那么準光學就是基于高斯波束的理論，高斯波束是光線概念的延伸。

2 討論

基于高斯波束的波束波導理論是由激光束的準直理論發展而來，因為激光器的出射光束是高斯波束。將高斯波束理論用于毫米波傳輸產生了毫米波光學，將其應用于太赫茲波段是毫米波光學的直接推廣。雖然在毫米波段已經有成熟的透鏡天線投入使用［7］，但波束波導系統和透鏡天線設計仍然有許多問題，需要進一步研究。使用準光技術只是部分的解決了高斯波束傳輸問題，但隨之也帶來了新的問題，其中包括:透鏡天線的介質損耗和透鏡表面反射引起的傳輸效率的降低;由于透鏡在軸上和邊緣厚度的差異，當波穿過透鏡時，引起不同位置的損耗不同，進而導致場分布的失真。如果考慮波從透鏡表面的反射，問題可能變得更加復雜，比如當波從波束軸方向入射時，是正入射，而從邊緣方向入射時，是斜入射。入射角度的不同會帶來反射率的不同，這些因素都會降低波的傳輸效率，引起波前的失真，以及計算誤差。因此，在透鏡天線設計中，還必須考慮表面涂層，通過涂層的多級反射抵消反射能量，或者通過表面刻槽來抵消反射。為了避免反射以及透射引起的損耗，可以采用偏軸反射鏡［8］。在涉及到陣列應用時，可以按照圖4 所示的原理用一個大透鏡照射很多個天線，也可以用很多個小半球透鏡，每個半球透鏡照射一個天線［9］。

透鏡天線的另一個問題是帶寬問題。從前面的透鏡設計理論可以看出，透鏡天線的表面曲率與波長關系密切，為某一波段設計的透鏡天線并不適合于其它波段，即波束波導系統具有很窄的帶寬。如果需要使用波束波導系統傳輸寬帶信號，如在通信系統中經常需要進行寬帶傳輸，波束波導天線的窄帶寬可能在寬帶通信系統中的應用受到限制。為了擴展透鏡天線的帶寬，也需要通過表面刻槽等方式來提高帶寬［1］。

總之，隨著太赫茲技術的深入研究，以及太赫茲應用的逐漸普及，高斯波束理論，以及建立在波束波導系統基礎之上的透鏡設計方法會不斷的得到改進。對于科技工作者來說，需要探究的問題也將會層出不窮。

3 未來可能進一步研究的科學問題

3.1 太赫茲陣列技術

太赫茲波長短，器件尺寸小，常規工藝手段無法滿足精度要求，因此需要采用硅基MEMS 集成加工工藝。如果將半導體工藝和硅基MEMS 工藝結合起來，制作太赫茲器件陣列是一個自然的選擇。當使用陣列技術處理太赫茲問題時，一個不可回避的問題是如何利用陣列技術進行大功率合成和陣列接收機的應用，特別是在陣列技術中可能用到的功率分配技術，可能成為未來的研究熱點。單個功率器件的輸出功率小，如Impatt，Gunn 管。為了得到大功率，可采用空間合成技術，其設計原理如圖4 所示。太赫茲波通過準光系統進入功分器，將信號功率等分成多個通道，在每個陣列單元實現信號處理，陣列中每個電路具有低功率特性。功分器為每個電路提供小部分的輸入功率，功率合成器收集所有電路的輸出合成輸出信號。

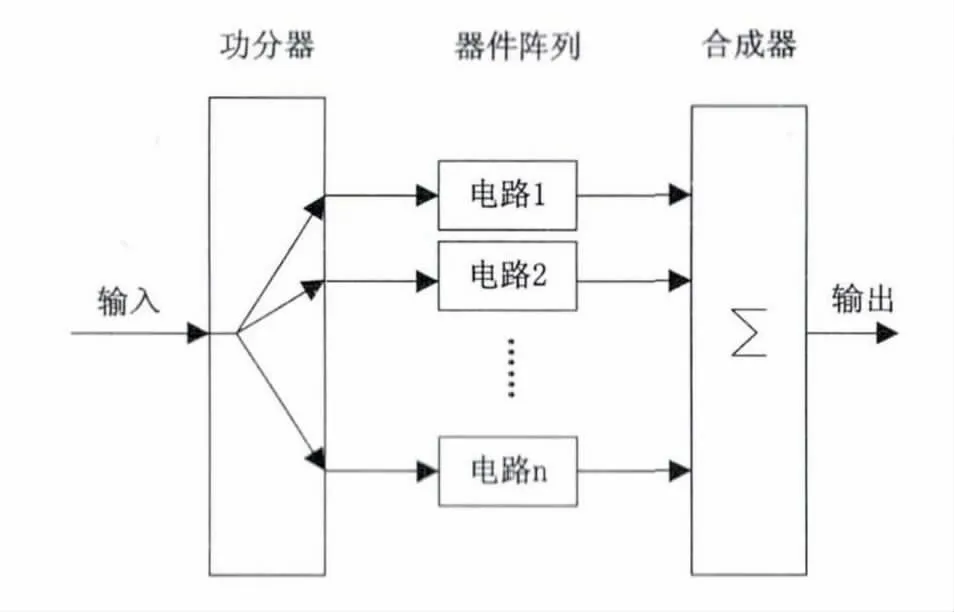
圖4 用準光陣列實現空間功率合成

根據上述結構和所使用的電路形式，可以實現下列功能:如果陣列單元是放大器，則電路實現功率合成;如果陣列單元是倍頻器，則電路實現高功率信號源;如果陣列單元是混頻器，則電路實現陣列接收。在上述結構中，功分器和合成器是一對互易器件，是準光陣列中最關鍵的器件。只有高效的實現功率分配和功率合成才能最大限度的發揮出陣列的優勢，這里“高效”是指以極低的損耗進行功分和合成。在高頻段(毫米波、太赫茲波段以上)，目前這種高效的功分器和合成器是缺失的，可實現的單元電路也是極少的，而這些地方正是科技工作者大有作為的領域。

對于陣列的基本要求是:陣列中的單元是等距離的，陣列是線性陣列或者平面陣列，每個單元類型的結構相同，接收相等的功率，而且每個單元最好是等幅和同相。對于輸出合成，也希望每個陣列單元是等幅同相，如果采用傳輸線技術實現功率分配和單元互聯，不僅損耗大，而且導致結構復雜。在陣列應用中，采用準光技術是較好的選擇。

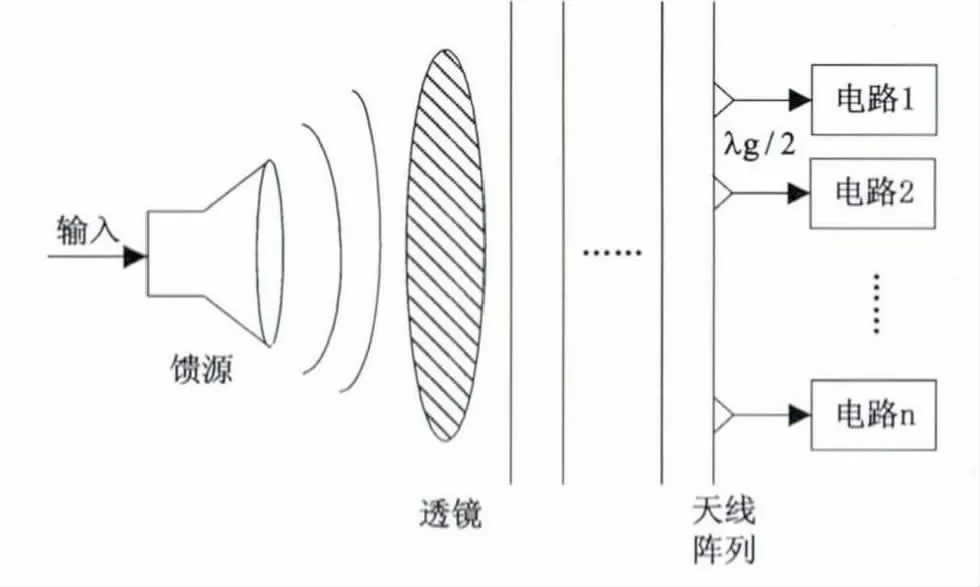
圖5 采用準光技術實現功率分配

準光功分器的原理框圖如圖5 所示。它通過波束饋電系統接收輸入功率，輸入波束通過饋源輻射，波束通過準光系統后，輸入波束的波前獲得了指定的相位分布。當波束離開準光系統時，波前變成了平面波，在天線陣列平面上形成均勻的相位分布。在天線陣列平面上，可對場分布進行空間采樣。假設單元之間的間距小于自由空間波長的一半，由傅里葉光學和采樣定理可知，入射波功率以最小的損耗耦合進陣列單元中，在均勻分布假設下，所有陣列單元接收相等的功率。該假設存在幾個問題:通常電路的物理尺寸高達幾個波長，不能滿足λg/2 間距要求;太赫茲器件和電路，特別是天線的物理尺寸不能做到最小化，限制了功分器在這些頻段上的應用;如何設計口徑尺寸為半個波長的天線且天線間距滿足半波長要求將是天線陣列應用的難題。

3.2 光學矩陣在太赫茲波段的應用問題

按照光線光學理論，一條入射光線產生唯一一條出射光線，一條光學光線通過一個光學系統的行為可以用光學系統的光線矩陣進行預測。例如，對平面P1 上的一條入射光線來說，可以用光線的斜率和它到光軸的距離來描述，如果光學系統的光線矩陣(ABCD 矩陣)已知，那么它的出射光線就是已知的，這是人們熟知的光線理論。當將光線理論用于高斯波束時，等價的說法是，如果入射光束的束腰是已知的，那么通過光線矩陣可以預測出射光線的束腰，這個結論對于光學系統，以及對于高斯光束是成立的，并且光學透鏡系統是按照光線理論設計的。

如圖6 所示，如果已知P1 平面是高斯波束，束腰已知，當它通過光學系統后，仍然是高斯波束，因此只要知道出射平面P2 上的束腰，P2 平面上的口徑分布就是已知的。在圖6 中，假設P1 平面上的口徑分布可以用高斯波束來近似，在經過一個純光學系統后，在平面P2 上的口徑分布也是高斯波束。為了得到P2 平面上的高斯波束參數，可以使用光學矩陣(ABCD 矩陣)來預測，假定光學系統中的透鏡是按照光線理論設計的。如果讓太赫茲波通過同一個光學系統，那么設想是否也能預測出P2 平面上的口徑分布也是高斯分布，或者說，能否按照準光系統理論設計透鏡，然后利用ABCD 矩陣來預測P2 平面上的口徑分布。

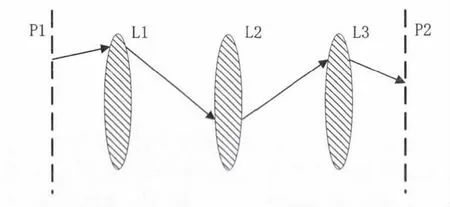
圖6 高斯波束通過光學系統的變化

當將光線理論用于THz 波段時，我們是否需要對上述理論進行修正。或者說，為了使得上述理論在太赫茲波段依然成立，透鏡系統需要按照光線理論來設計成光學透鏡，還是需要按照準光理論設計成準光透鏡。是否需要建立一種新的準光學矩陣理論。是否能夠將光線光學完全移植到太赫茲波段。上述問題將是使用準光理論解決THz 波傳輸應用而需要進一步研究的課題。

3.3 傅里葉光學

按照傅里葉光學方法，如果將一個物體放置在一個光學透鏡L 的前焦平面上，經過透鏡L 后，那么在它的后焦平面上的圖案是物體的傅里葉變換。透鏡L 起傅里葉變換的作用，相應地，L 稱為傅里葉變換透鏡。如果將上述傅里葉變換的思想應用于太赫茲波段，將一個高斯波束的束腰放置在透鏡L 的前焦平面上，經過透鏡后在它的后焦平面上是否會形成高斯波束。因為高斯波束的傅里葉變換仍是高斯波束，在傅里葉變換準光透鏡的后焦平面上也形成高斯波束，且束腰位置恰好位于后焦平面上。這種預測是否準確可靠，在傅里葉光學中，透鏡L 是按照光線理論設計的光學透鏡。如果上述問題能夠得到肯定的答案，那么在太赫茲波段，透鏡L 是光學透鏡，還是準光透鏡，還是其它類型的透鏡。

在傅里葉光學中，上述透鏡所起的作用是電磁波近場到遠場的變換，或者反過來，是遠場到近場的變換。對于電磁波遠場來說，可以認為電磁波在自由空間是TEM 波，即電場強度矢量與傳播方向垂直，在傳播方向z 上沒有電場分量，即?Ε(x，y，z)/?z=0。對于太赫茲波來說，高斯波束也有近場與遠場的概念，但高斯波束的近場與遠場不同于平面電磁波的近場和遠場，即高斯波束不是橫電磁波，那么如果將一個高斯波束的束腰放置在傅里葉變換透鏡L的前焦平面上，在它的后焦平面上是否得到高斯波束的遠場，或者其它類型的場，是否能滿足橫電磁波的假設條件，即在P2 平面上?Ε(x，y，z)/?z=0 成立。以上問題仍是準光理論應用于THz 波中需要深入研究的問題。

4 結束語

本文從太赫茲波的傳輸所面臨的挑戰出發，討論了用自由空間替代波導傳輸太赫茲波的問題。太赫茲波在金屬波導中傳輸損耗大，因此可選擇使用自由空間作為傳輸介質，以實現大寬帶的太赫茲波信號低損耗的傳輸。太赫茲波傳輸系統器件的尺寸小，往往只有幾倍的波長大小。需要使用高斯波束理論來設計透鏡系統。高斯波束不同于光線光學，高斯波束球面波的焦點是離散的分布在波束軸上，因此，在光路傳輸和透鏡設計中需要進行改進。

最后，針對太赫茲波傳輸在實際應用的局限性，本文探討了使用準光理論實現太赫茲波傳輸的技術和方法。限于作者在天線理論和光學知識等方面的不足，我們歡迎各行專家的指正和討論，以進一步推動我國太赫茲科學的發展及其實際應用。

［1］Michael J.Leeson，The application of Quasi-optical techniques to millimeter wave radar［D］.PhD Thesis，University of St Andrews，1993.

［2］陳鶴鳴，施偉華等，光子學——現代通信光電子學［M］.北京：電子工業出版社，2009.

［3］J.C.G.Lesurf，Millimetre-wave optics，Devices and Systems［M］.Adam Hilger，Bristol and New York，1990.

［4］竇文斌編著.毫米波準光理論與技術［M］.第二版，北京：高等教育出版社，2006.

［5］俞俊生，陳曉東編著.毫米波與亞毫米波準光技術［M］.北京：北京郵電出版社，2010.

［6］王元源，李春化，袁晶.毫米波/亞毫米波準光饋電系統設計［C］.第一屆全國太赫茲科學技術與應用學術交流會論文集(下冊)，中國北京：2012：363-373.

［7］Qiu Jinghui，Zhuang Zhong，Lu Kai，et al.，Design and measurement of Quasi-optics for millimeter wave imaging system［C］.International Workshop on Imaging Systems and Techniques，Sept.China，2009.

［8］D.Filipovic，G.Gauthier，S.Raman，and G.Rebeiz，Off-axis properties of silicon and quartz dielectric lens antennas ［J］.IEEE Trans.Antennas Propag.，1997，45：760-766.

［9］Tom Nitta，Masato Naruse，Yutaro Sekimoto，et al.Beam pattern measurements of millimeterwave kinetic inductance detector camera with direct machined silicon lens array［J］.IEEE Transaction on Terahertz Science and Technology，2013，3(1) ：56-62.