光學讀出紅外成像中面光源影響下的光學檢測靈敏度研究*

吳健雄 程騰張青川高杰 伍小平

(中國科學技術大學,中國科學院材料力學行為和設計重點實驗室,合肥 230027)

1 引言

紅外成像技術在軍事、醫學、氣象、公共安全等領域有廣泛的應用前景.近年來,隨著微機電系統(micro-electromechanical systems,MEMS)技術的發展,基于雙材料微懸臂梁熱機械效應的非制冷紅外成像技術逐漸受到重視.在紅外信號的檢出方法上,研究者先后提出了電容、壓電、光學等多種方案.相對于其他檢出方案,光學讀出原理不需要在焦平面陣列(focal plane array,FPA)中集成微讀出電路,因此,它對MEMS加工工藝要求低,制作難度小,是一種具有低成本、高性能潛力的解決方案.美國Berkeley大學的研究小組開展了基于光學干涉讀出方式的雙材料微懸臂梁FPA研究,并獲得了人體的熱圖像[1,2].Nikon公司在2001年和2002年陸續報道了檢測熱變形所致懸臂梁轉角的光學讀出系統[3,4],并得到了室溫下的人像.2005年,Redshift Systems公司報道了一種薄膜熱可調諧濾波片FPA,獲得了噪聲等效溫度差(noise equivalent temperature difference,NETD)小于1 K的人體熱像[5].2006年,美國Oak Ridge國家實驗室的研究小組設計了“青蛙”狀雙材料微梁FPA,利用小孔濾波成像光路,成功獲得NETD約為500 mK的人體紅外圖像[6].2009年,美國貝爾實驗室報道了他們基于像素間干涉原理的光學讀出系統[7].同年,美國Agiltron,Inc.公司也報道了他們在研發商業化的光學讀出熱型紅外檢測器方面的進展[8].

從2001年開始,本課題組開展了基于雙材料微懸臂梁陣列的光學讀出非制冷紅外成像技術研究,提出了在FPA譜平面上進行刀口濾波的光學讀出方法[9,10],以及回折腿間隔鍍金結構的微梁單元設計[11];同時,針對傳統的有基底FPA結構的不足,設計并實現了全新概念的無基底FPA[12].截至目前,課題組已先后制作了多批次、微梁單元長度分別為200,120,60,50,30μm的無基底FPA[12-16],實現了室溫物體的紅外成像,獲得的最高系統級NETD已達100 mK[16],接近現有商用非制冷紅外熱像儀的典型指標,并在此基礎上成功實現了系統集成,制作出了小型化樣機.

在光學檢測靈敏度的理論分析中,通常將實際使用的具有一定尺寸大小的發光二極管(LED)面光源簡化為理想點光源[10,17].這種近似簡化雖然便于研究者分析反光板的物理尺度特征(長度、彎曲曲率、粗糙度等)與光學檢測靈敏度之間的關系,但與實際不符.對此,本文通過將實際使用的LED面光源等效為發光均勻的圓形面光源,利用夫瑯禾費衍射理論,建立了圓形面光源調制下的光學檢測靈敏度模型(簡稱面光源模型),分析了圓形面光源的半徑、反光板長度與光學檢測靈敏度的關系,并給出了光源半徑和反光板長度的最優化準則.

2 光學讀出紅外成像技術的基本原理

本課題組提出的無基底FPA結構[18]如圖1所示,FPA上各微梁單元直接生長在一層單層膜的無基底支撐框架上.每個微梁單元由紅外反光板(吸收板)、雙材料變形梁、熱隔離梁三部分構成.紅外反光板一側為SiNx膜,用于吸收紅外輻射,另一側為Au膜,用于反射由LED面光源發射的讀出光.雙材料變形梁由SiNx和Au兩種材料構成,由于這兩種材料熱膨脹系數的巨大差異,溫度變化后將產生熱致彎曲變形,并使反光板發生偏轉,進而導致反光板的衍射譜移動,從而被光學讀出系統檢出[10].

本課題組提出的基于空間刀口濾波的光學讀出系統[18]如圖2所示:LED面光源位于準直透鏡前焦面,發出的光束經準直透鏡后變為與光軸平行的準直平行光,到達半透半反鏡,反射光入射到真空室內的FPA上,被FPA微梁單元反光板反射,經過傅里葉透鏡后在刀口平面形成衍射譜.當對紅外目標成像時,FPA吸收輻射導致微梁單元溫度升高,雙材料變形梁發生彎曲,使反光板偏轉角發生變化,其在刀口譜平面的衍射譜相應移動,通過刀口濾波器的光量也隨之改變,即將微梁單元反光板偏轉角變化轉變為CCD接收到的光強信號的變化.而反光板偏轉角變化大小取決于FPA吸收的紅外輻射量,因此熱物體不可見的紅外像最終轉變為CCD上可見的灰度圖像[19].

圖1 無基底FPA結構原理

圖2 紅外成像系統原理

為了便于分析,通常將LED面光源簡化為理想點光源,其在刀口譜平面的光強分布可表述為[10]

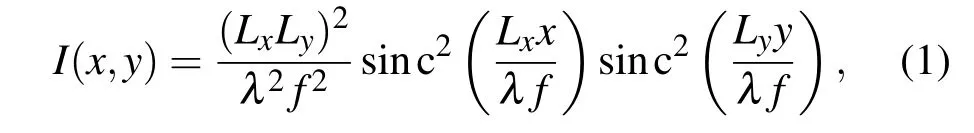
其中,Lx和Ly是無基底FPA微梁單元反光板(紅外吸收板)的寬度和長度(如圖1).λ為LED面光源發射的光波長,f為傅里葉變換透鏡的焦距.

根據光學檢測靈敏度的定義[10]:FPA像素反光板單位轉角(dθ)引起CCD接收到的光強變化(dI),即 dI/dθ.當不考慮反光板的彎曲變形和初始轉角等復雜因素,理想點光源的光學檢測靈敏度為[10]

由于實際使用的LED光源是具有一定尺寸的非相干均勻面光源,上述基于理想點光源假設的理論模型與實際不符.因此,本文通過將實際的LED面光源等效為發光均勻的圓形面光源,建立更加精確的光學檢測靈敏度模型分析,并進行了相關實驗驗證.

3 面光源影響下光學檢測靈敏度的理論研究

3.1 面光源影響下任意點的光強分布

為了便于分析,將圖2的光讀出光路示意圖等效為圖3所示的光路剖面圖.

圖3 等效光路圖 笛卡爾坐標系下FPA平面為MON,圓形LED光源半徑為r,準直透鏡L1和傅里葉變換透鏡L2的焦距均為 f,光源平面UO1V和刀口譜平面XO2Y分別是L1的前焦面和L2的后焦面,譜平面XO2Y上曲線a為理想點光源形成的衍射譜,曲線b為光源平面UO1V上(u,v)點形成的衍射譜,曲線c為LED面光源整體形成的衍射譜

由于實際使用的LED面光源為非相干均勻面光源,因此可將其等效為無數點光源的線性疊加,且這些點光源光強相等,呈圓形分布,半徑為r(圖3右上角所示),其中處于準直透鏡L1前焦點位置O1上的點光源即為(1),(2)式所述的理想點光源.同時,由于實際使用的LED面光源尺寸遠遠小于準直透鏡的焦距(r/f＜0.01),可以近似認為各點光源位于理想點光源(0,0)的微小鄰域內,因此,微小鄰域內任意位置(u,v)的點光源經過準直透鏡L1后仍可近似為平行光,其衍射譜的形狀、大小與理想點光源(0,0)的衍射譜相同,僅發生了整體性的微小平移(如圖3中刀口譜平面上曲線a和b).基于(1)式,容易得到點光源(u,v)在刀口平面所形成的光強分布為

由于刀口濾波器沿Y方向濾波,因此對(3)式沿X軸從-∞+∞積分,其中歸一化sinc函數積分公式為

利用(4)式可以得到通過刀口濾波器沿Y方向(濾波方向)的光強分布:

當FPA吸收紅外輻射,產生轉角為θ(逆時針方向為正)時,由光杠桿原理可知刀口平面的光譜整體向上移動2θf[16,17],此時刀口譜平面的光強分布為

3.2 面光源影響下的光學檢測靈敏度

根據(6)式,半徑為r的圓形均勻面光源在刀口譜平面所形成的光強分布可通過在圓形區域內積分得到:

對(7)式歸一化,可得:

(8)式表述了半徑為r的圓形均勻面光源在刀口譜平面上Y方向(濾波方向)的光強分布,即圖3中刀口譜平面上曲線c.

刀口濾波器濾波沿Y方向濾波,其濾波位置為y=y0,根據光學檢測靈敏度的定義,得到歸一化后最高光學檢測靈敏度(當不考慮反光板彎曲等因素時,刀口濾波位置y0位于衍射譜正中心[17]),簡稱為光學檢測靈敏度:

4 面光源影響下光學檢測靈敏度分析優化及實驗驗證

4.1 面光源在刀口譜平面光強分布

實驗使用的LED光源為單色綠光光源,波長范圍在490—560 nm之間,峰值約為500 nm,因此在下文分析時,將LED光源波長λ等效為500 nm.根據(8)式,得到當反光板長度一定(Ly分別為50,100,150,200μm)時,不同半徑大小(r=0—1 mm)的面光源在刀口譜平面的歸一化光強分布,如圖4所示.

可以看出,光源半徑r=0曲線(圖4中紅色曲線)在譜中心處的光強分布最集中,r=0.5 mm(圖4中黃色曲線)時次之,r=1 mm(圖4中綠色曲線)時光強最為分散.即光源半徑r越小,位于譜中心的光強越集中,濾波后光強的變化越大,根據光學檢測靈敏度的定義,此時得到的光學檢測靈敏度越高.

同時隨著反光板長度Ly增大(50,100,150,200μm分別對應圖4(a),(b),(c),(d),光源半徑r=0時的紅色曲線與r=1 mm時的綠色曲線的峰值差距增大,即減小光源半徑r帶來的光強集中分布程度增加,對光學檢測靈敏度的影響也相應增大.

4.2 光學檢測靈敏度分析及優化

根據(9)式,得到不同光源半徑尺寸(r=0—1.5 mm)和不同反光板長度(Ly=0—200μm)與光學檢測靈敏度之間變化關系,如圖5所示.

圖5(a)和(b)分別是光學檢測靈敏度Dmax隨FPA反光板長度Ly和光源半徑尺寸r變化曲面的兩個不同方向視圖,可以看出:

圖4 不同FPA反光板長度Ly下歸一化光強Inormalized與光源尺寸r的關系,其中λ=500 nm,f=100 mm (a)Ly=50μm;(b)Ly=100μm;(c)Ly=150μm;(d)Ly=200μm

圖5 面光源影響下光學檢測靈敏度Dmax與光源尺寸r和FPA反光板長度Ly的關系,其中λ=500 nm,f=100 mm(a)Ly方向視圖;(b)r方向視圖;(c)不同反光板長度Ly理論實驗對比;(d)不同光源半徑r理論實驗對比

1)當光源半徑r=0時,光學檢測靈敏度Dmax隨反光板長度Ly線性單調上升(即圖5(a)中r=0曲線),與理想點光源模型推導出的(2)式描述一致,即理想點光源模型是面光源模型下光源半徑r=0(光源半徑無窮小)的特例;

2) 當光源半徑r＞0時,光學檢測靈敏度Dmax隨反光板長度Ly非線性增加,且增速逐漸放緩,最終趨于某一極限值,例如,當r=0.5 mm時,極限值約為4(1/(?)),當r=1.0 mm時,極限值約為2(1/(?)).

3) 當反光板長度Ly一定時(圖5(b)),光學檢測靈敏度Dmax隨著面光源半徑r的減小而大幅提高,在r=0(理想點光源)時取得極值;并且反光板長度Ly越大,光源半徑r對光學靈敏度Dmax的影響越大.

根據面光源模型可知,當反光板長度一定時,LED光源半徑越小,光學檢測靈敏度越高,同時所需光強越大,即要求LED功率越大.因此,必須在光源功率和光學檢測靈敏度之間權衡,本文定義最優化的光源半徑roptimize為理想點光源(即光源半徑r=0時)的光學檢測靈敏度值90%所對應的面光源半徑.同理,當光源半徑一定時,FPA反光板長度越大,光學檢測靈敏度越高并逐漸趨近于某一極限值;同時微梁單元尺寸越大,紅外成像的空間分辨率越低.在空間分辨率和靈敏度之間權衡,將FPA反光板優化長度上限閾值Lupper-limit定義為此極限值的90%對應的反光板長.

4.3 不同FPA反光板長度的實驗驗證

針對面光源模型,利用反光板長度Ly分別為180,90,50μm的FPA進行了光學檢測靈敏度的驗證實驗,實驗參數為:r=0.5 mm,λ=500 nm,f=100 mm,結果如圖5(c)中藍色標點所示.為了便于對比分析,圖中還同時顯示了r=0(即理想點光源模型)的理論值(紅色曲線),r=0.5 mm的理論值(綠色曲線)的對比曲線.

可以看出,理想點光源模型(r=0時)理論值隨著反光板長度Ly增加而線性增加,與實驗值的變化趨勢有較大差異,特別是當反光板長度Ly＞50μm時,與實驗值相比相差甚遠.面光源模型光源半徑r=0.5 mm的理論值隨著Ly增加而逐漸趨于某一極限值,并且當Ly=50μm和Ly=90μm時均與實驗值符合得較好,但當Ly=180μm時與實驗值有一定差異,這是由于實驗誤差以及FPA反光板的初始彎曲較大而導致衍射譜的彌散[10,17],從而降低了光學檢測靈敏度.

根據面光源模型,如圖5(c)所示,當r=0.5 mm,λ=500 nm,f=100 mm時,FPA反光板優化設計長度上限閾值Lupper-limit約為60μm(即圖5(c)中r=0.5 mm曲線極限值的90%對應的反光板長).

4.4 不同光源半徑的實驗驗證

針對面光源模型,采用不同光源半徑(r=0.3—0.5 mm,間隔為0.1 mm)的LED面光源進行紅外成像實驗驗證,實驗參數為:Ly=50μm,λ=500 nm,f=100 mm,結果為圖5(d)中的藍色曲線,為了便于對比,圖5(d)中的紅色曲線為Ly=50μm時的理論值曲線.

實驗結果符合理論預期:當圓形面光源的半徑r為0.3 mm時候,靈敏度下降到理想點光源的90%;當半徑r到0.5 mm時候,靈敏度下降到理想點光源的80%;而當光源半徑尺寸r到了1.0 mm的時候,光學檢測靈敏度已經下降到理想點光源的55%.

根據面光源模型,當Ly=50μm,λ=500 nm,f=100 mm時,最優化光源尺寸為roptimize=0.3 mm(即圖5(d)中理想點光源的90%對應的面光源半徑).

5 結論

本文通過將LED面光源等效為圓形均勻面光源,利用夫瑯禾費衍射理論建立了面光源模型進行理論研究,并針對不同半徑面光源和不同反光板長度FPA進行了實驗驗證.理論分析和實驗結果表明:光學檢測靈敏度隨光源半徑的減小而提高,隨反光板長度的增加而逐漸趨近于某一極限值.在此基礎上,本文進一步提出了面光源影響下反光板長度的優化設計建議,當光源半徑r=0.5 mm時,FPA反光板優化設計長度上限閾值為60μm;同時定義了面光源影響下光源半徑的最優值,當Ly=50μm時該值為0.3 mm.按照目前采用圓形面光源半徑典型值為0.5 mm推論,隨著LED光源技術的提高,采用發光均勻性更好、持續穩定發光強度更高的LED光源能夠將光學讀出靈敏度提高10%—20%.

[1]ZhaoY,MaoM,HorowitzR,MajumdarA,VaresiJ,NortonP,Kitching J 2002 J.MEMS 11136

[2]Mao M,Perazzo T,Kwon O,Majumdar A,Varesi J,Norton P 1999 Proc.IEEE MEMS 100

[3]Ishizuya T,Suzuki J,Akagawa K,Kazama T 2001 J.I.Image Inform.Television Eng.55304

[4]Ishizuya T,Suzuki J,Akagawa K,Kazama T 2002 Proc.IEEE MEMS 578

[5]Wu M,Cook J,DeVito R,Li J,Ma E,Murano R,Nemchuk N,Tabasky M,Wagner M 2005 Proc.of SPIE 5783496

[6]Grbovic D,Lavrik N V,Datskos P G,Forrai D,Nelson E,Devitt J,Mclntyre B 2006 Appl.Phys.Lett.89073118-1

[7]Jones C D W,Bolle C A,Ryf R,Simon M E,Pardo F,Aksyuk V A,Lai W Y C,Bower J E,Miner J F,Klemens F P,Cirelli R A,Sorsch T W,Ferry E J,Fetter L A,Pai C S,Taylor J A,Vyas B,Watson G P,Stekas B,Baker M R,Papazian A R,Basavanhally N R,Mansfield W M,Kornblit A,Keller R C,Gates J V,Ramirez A P 2009 Sensors Actuators A 15547

[8]Erdtmann M,Zhang L,Jin G,Radhakrishnan S,Simelgor G,Salerno J 2009 Proc.SPIE 7298

[9]Pan L,Zhang Q C,Wu X P,Duan Z H,Chen D P,Wang W B,Guo Z Y 2004 Experiment.Mech.19403(in Chinese)[潘亮,張青川,伍小平,段志輝,陳大鵬,王瑋冰,郭哲穎2004實驗力學19403]

[10]Duan Z H,Zhang Q C,Wu X P,Pan L,Chen D P,Wang W B,Guo Z Y 2003 Chin.Phys.Lett.202130

[11]Miao Z Y,Zhang Q C,Chen D P,Wu X P,Li C B,Guo Z Y,Dong F L,Xiong Z M 2006 Acta Phys.Sin.553208(in Chinese)[繆正宇,張青川,陳大鵬,伍小平,李超波,郭哲穎,董鳳良,熊志銘2006物理學報553208]

[12]Miao Z Y,Zhang Q C,Chen D P,Guo Z Y,Dong F L,Xiong Z M,Wu X P,Li C B,Jiao B B 2007 Ultramicroscopy 107610

[13]Dong F L,Zhang Q C,Chen D P,Miao Z Y,Xiong Z M,Guo Z Y,Li C B,Jiao B B,Wu X P 2008 Ultramicroscopy 108579

[14]Dong F L,Zhang Q C,Chen D P,Miao Z Y,Xiong Z M,Guo Z Y,Li C B,Jiao B B,Wu X P 2007 Chin.Phys.Lett.243362

[15]Dong F L 2007 Ph.D.Dissertation(Hefei:University of Science and Technology of China)(in Chinese)[董鳳良2007博士學位論文(合肥:中國科學技術大學)]

[16]Zhang Q C,Miao Z Y,Guo Z Y,Dong F L,Xiong Z M,Wu X P,Chen D P,Li C B,Jiao B B 2007 Optoelectron.Lett.3119

[17]Shi H T,Zhang Q C,Qian J,Mao L,Cheng T,Gao J,Wu X P,Chen D P,Jiao B B 2009 Opt.Express 174367

[18]Cheng T,Zhang Q C,Jiao B B,Chen D P,Wu X P 2009 J.Opt.Soc.Am.A 262353

[19]Cheng T,Zhang Q C,Chen D P,Shi H T,Gao J,Qian J,Wu X P 2010 Chin.Phys.B 19010701