高斯-謝爾模光束在大氣湍流中傳輸的相干特性研究*
李成強1)2)? 張合勇1)王挺峰1)劉立生1)2)郭勁1)
1)(中國科學院長春光學精密機械與物理研究所,激光與物質相互作用國家重點實驗室,長春 130033)
2)(中國科學院大學,北京 100049)
1 引言
長久以來,激光相干特性和激光束的方向性被認為是直接關聯的.然而,在1970年前后,理論和實驗證明激光束方向性好并不意味著空間相干性高,這一發現引起了對部分相干光源的研究熱潮[1].在部分相干光源中,有一種比較特殊的光源被稱為高斯-謝爾源,因為該光源產生的光束遠場光場強度分布和完全相干高斯光束一樣[2].相干光在湍流介質中傳輸時,湍流會增加波前的隨機性,使相干光以部分相干光的形式存在[3].另外,激光器自身因素往往造成激光束以多模的形式存在,多模激光輻射以部分相干的高斯-謝爾模型(GSM)光束形式存在[4].因此,對部分相干光的研究具有一定的實際意義.鑒于激光的應用需求,有必要闡明部分相干光源在湍流介質中的傳輸特性.目前的研究工作側重于分析湍流介質對激光強度分布、空間相干性和偏振特性的影響[5-14].橫向相干長度(相關長度)是空間相干性的直接反映,因此,對相干長度變化的研究有助于理解激光傳輸時空間相干特性及偏振特性的變化.Wu和Boardman[15]分析了相干長度、光源尺度同量級的GSM光束的傳輸特性,研究結果表明,光束在真空中傳輸時,其橫向相干長度會緩慢增加,而在湍流中的傳輸會造成橫向相干長度的減小.Friberg和Sudol[9]討論了GSM光束在真空中傳輸時空間相干特性的變化,研究發現對于GSM光束,在真空中傳輸時橫向相干長度與光斑尺度比值恒定不變.為保證部分相干光源的部分相干性,通常相干長度比光源尺度具有更小數量級[16],且研究大氣湍流對相干長度的影響有必要排除光源擴展的影響.Friberg在討論相干長度的變化時,雖排除了光源擴展的影響,但文章只討論了光束的真空傳輸.出于應用需求考慮,有必要對湍流中部分相干光的傳輸做進一步分析.
本文以GSM光束為對象,根據廣義惠更斯-菲涅耳原理推導出該光束傳輸時的交叉譜密度函數表達式,并根據該表達式分析了GSM光束傳輸時橫向相干長度的變化情況,討論了光源參數和湍流介質對橫向相干長度變化所起的作用.在研究大氣湍流對相干長度的影響時,為排除光源擴展的影響,分析了GSM光束在湍流介質中傳輸時橫向相干長度與光斑尺度的比值,由此得出有助于部分相干光大氣傳輸理論分析和實驗的一些推論.
2 理論分析
將光場視為隨機場u(r,ω),該隨機場可以用平穩隨機過程理論進行分析,其交叉譜密度函數定義為[5]
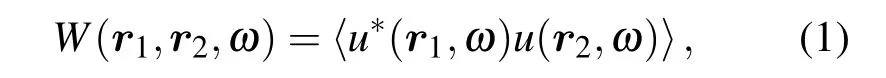
式中星號表示復共軛,尖括號表示系宗平均.對于給定的光源交叉譜密度W(0)(ρ1,ρ2;ω),根據廣義惠更斯-菲涅爾原理可以得到任意平面(z=const)上T1=(r1,z>0),T2=(r2,z>0)兩點處的交叉譜密度函數[5]:

上式中,〈···〉m記為湍流介質的統計平均,并對其做如下近似[17]:

其中M為

式中Φn(κ)為折射率波動的功率譜,本文選用Tatarski譜[5]:

其中l0,L0分別表示湍流內尺度和外尺度,為折射率結構常數.

現在考慮具有高斯型光強分布和相干性分布的高斯-謝爾源產生的隨機光場.光源面處交叉譜密度可表示為[18]上式中,參數I0及σ0,δ0分別為光源的光強、光斑尺度和相干長度.一般來說,為了保證光束具有部分相干特性,相干長度δ0的值要比光斑尺度σ0小得多,通常它們不在一個數量級上[16].
將(5)式及(3)式代入(2)式,可得

對上式進行冗長的積分運算,可得高斯-謝爾光束傳輸時交叉譜密度函數W(r1,r2,z;ω)的表達式:

上述表達式在交叉譜密度定義及湍流理論的基礎上,經過相應數學自主運算而獲得,其中相應參數如下:
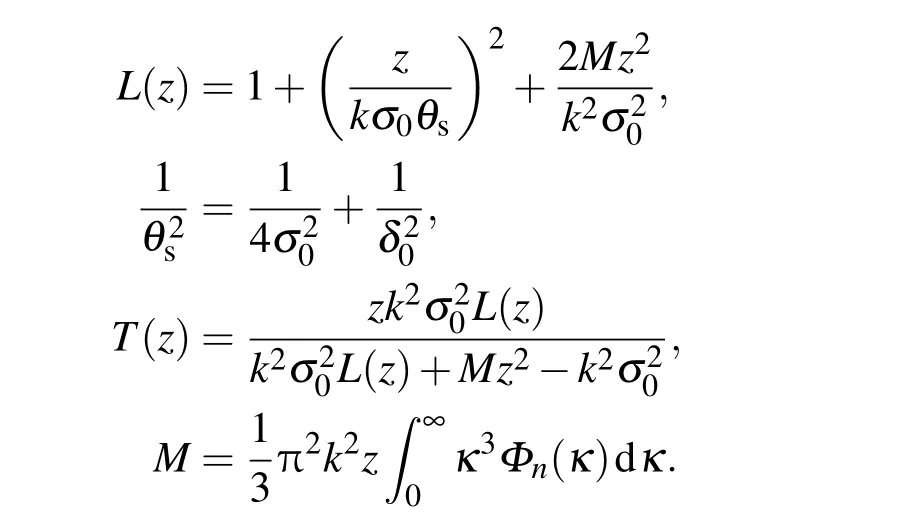
復相干度的表達式[19]:

將(7)式代入(8)式整理可得:


考慮復相干度的幅值,令

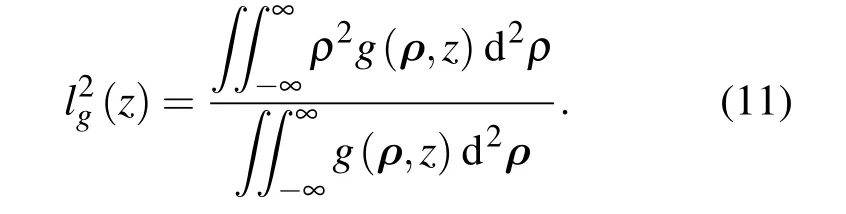

傳輸路徑上,平面z≥0處的光強度為
據此,可得

通過自主推導的交叉譜密度函數表達式,可得相干長度和光斑尺度的平方,計算得相干長度的平方為
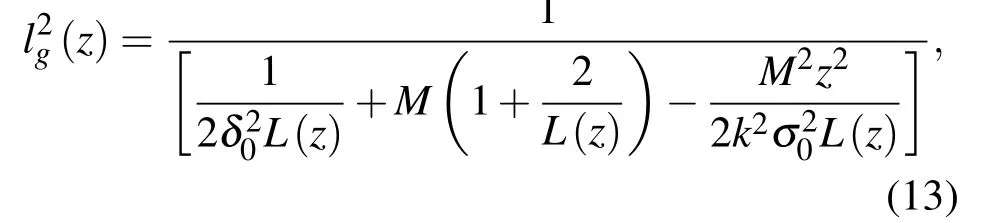
光斑尺度的平方為
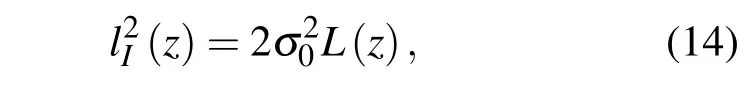
光束在真空中傳輸時,光斑尺度為

由上式可以看出,真空傳輸時光束擴展與σ0,δ0有關,光束擴展快慢主要由δ0決定.相干長度與光斑大小的比值α2[9]:
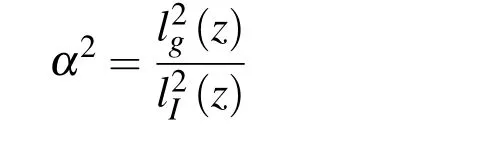

由(15)式可以看出,相干長度與光斑尺度的比值α與光源參數、湍流強度及傳輸距離有關,真空傳輸時,比值α為一確定值,這與Friberg研究GSM光束真空傳輸所得結果一致.但Friberg未對湍流中的光傳輸予以討論,本文將對這一傳輸問題進行分析.
3 數值計算結果與分析
通過表達式(13)可以看出,光源參數和湍流因素同時影響光傳輸時相干長度的變化.本文將對具有不同光源參數的光束在不同湍流條件下的傳輸進行數值計算,并給出理論分析.數值計算時參數的選取:湍流內尺度l0=5 mm,波數k=2π/λ=107.
圖1為光束在真空中傳輸時相干長度和光斑尺度的變化.圖1(a),(c)表明真空中傳輸時,對確定光源,相干長度和光斑大小隨傳輸距離線性增加;圖1(a),(b)反映了真空中光源參數對相干長度的影響,相干長度隨傳輸距離變化的快慢與光源大小有關,光源尺度σ0越大,相干長度增加越慢;圖1(c),(d)則反映了光源參數對光源擴展的影響,光源擴展的快慢主要由光源相干長度δ0決定,相干長度小的光源擴展快.
圖2為光束在湍流中傳輸時,相干長度和光斑尺度隨傳輸距離的變化.在湍流中,光源尺度及湍流強度對相干長度的影響較大,而光源相干性影響較小.由圖2(a),(e)可以看出,湍流中相干長度在傳輸距離較短時基本為線性增加,當傳輸距離較大時,相干長度隨著傳輸距離的增加而緩慢減小.對光束擴展的分析表明,湍流和光源相干性影響較大,而光源尺度對湍流中光束擴展影響較小.圖2(d),(f)表明光源相干性越差、湍流越強,傳輸過程中光束擴展越嚴重.通過以上分析可知,相干長度的變化受到光源參數和湍流強度的共同影響,其中光源參數的影響體現在光束擴展上.因此單純地分析相干長度的變化不足以反映光源參數和大氣湍流對光傳輸的影響.為排除光束擴展的影響,將利用相干長度和光斑尺度的比值進行分析.

圖1 真空中相干長度及光斑大小的變化(=0)(a)δ0=1 mm;(b)σ0=4 cm;(c)σ0=4 cm;(d)δ0=1 mm
圖3為光束在湍流中傳輸時相干長度與光斑尺度的比值隨傳輸距離的變化,結果表明:光束在湍流中傳輸時,對參數不同的光源,相干長度和光斑大小的比值均會減小;真空傳輸時,相干長度與光斑尺度比值為確定值,而當湍流存在時,相干長度與光斑尺度的比值同時受到光源參數和湍流強度的影響,該比值不再是一個確定的值;傳輸距離較小時,由于湍流影響小,此時與真空傳輸類似,比值α變化很小,當傳輸距離較大時,湍流影響明顯,比值α隨傳輸距離的增加而下降.圖3(a)中=10-14m-2/3,δ0=1 mm,通過改變比值β改變光源尺度大小,發現α的值在光傳輸一段距離后趨于一致;圖3(b)中=10-14m-2/3,σ0=4 cm,通過改變比值β改變光源相干長度大小,發現只有當光傳輸距離很遠時α的值才有可能趨于一致;圖3(c)中光斑尺度與相干長度比值不變,光傳輸一段距離后,相同位置處α的值會隨著光源尺度和相干長度的增加而增大.如果將傳輸過程中α的值發生較大變化的位置記為zc,通過圖3(d)可以發現,對確定的光源,zc的值會隨著湍流強度的增加而減小.
產生以上結果的主要物理原因是光束在湍流介質中傳輸時,光束波前會受到湍流影響,使波前隨機性增大,湍流越強,光束的波前受到的影響也將越明顯,波前隨機性將削弱原有波前相位的關聯性,而光波前相位的關聯性直接影響光束的相干性.因此,光束在湍流介質中傳輸時會因為湍流的作用而引起相干性下降.具有部分相干性的光束,其原有波前即具有一定的隨機性,但這種隨機性并不能減小湍流對光束現有波前的影響,因為湍流效應由湍流強度和傳輸距離共同決定,湍流引起的波前變化與光束原有波前相互獨立.光束在真空中傳輸時,自由衍射引起光束擴展,相干長度的變化受光束擴展影響而增加,這一點可以通過圖1看出.光束在大氣湍流中傳輸時相干屬性的變化由光源參數和湍流強度共同決定.當光束在湍流介質中傳輸距離較短時,湍流作用很小,以至于對光束引起的波前隨機性可以忽略.光源參數對光傳輸的影響占有主要地位,在這一距離內以自由衍射作用為主,光束擴展引起相干長度的增加,此時與自由空間傳輸類似,這一點可以由圖2(a),(e)看出.但隨著傳輸距離的增加,湍流效應增強并造成相干長度下降.
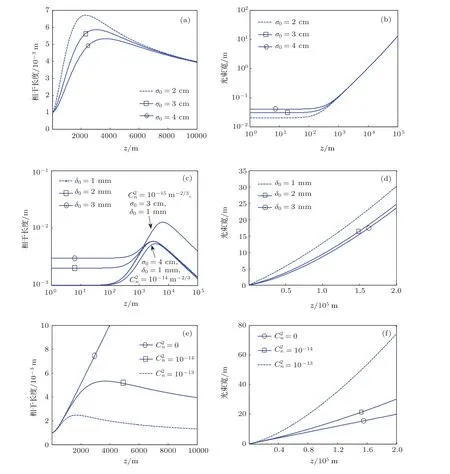
圖2 湍流中相干長度及光斑大小的變化 (a),(b)10-14m-2/3,δ0=1 mm;(c),(d)=10-14m-2/3,σ0=3 cm;(e),(f)δ0=1 mm,σ0=4 cm
4 結論
本文以部分相干的GSM光束為對象,根據廣義惠更斯-菲涅耳原理推導出GSM光束傳輸時交叉譜密度函數的解析表達式.基于該表達式數值分析了大氣湍流對相干長度的影響,并與真空中傳輸相干長度的變化做了對比,發現GSM光束在真空中傳輸時,影響相干長度變化的因素為光源參數,光束擴展造成相干長度增加,自由空間中光束擴展是光束自由衍射的結果;而在大氣湍流中傳輸時,相干長度的變化受光源參數和湍流的共同影響,結果表明,在傳輸距離較短時,光束傳輸特性與真空傳輸類似,相干長度因為光束擴展而增加,當傳輸距離較大時,湍流效應增強引起相干長度下降.因此,單純從相干長度方面分析大氣湍流帶來的影響不夠完備.為排除光源擴展的影響,本文利用相干長度與光斑尺寸的比值進行分析,發現對參數不同的光源,大氣湍流均會造成比值的下降,但比值下降的快慢與光源參數和湍流強度有關.上述結論不僅可以用于分析激光傳輸時的相干度問題,還可以用于普通的電磁光束傳輸領域.
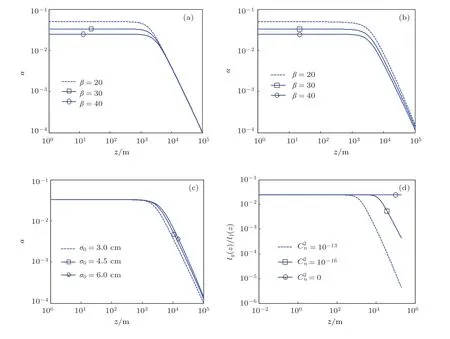
圖3 相干長度與光斑大小的比值(β=σ0/δ0)(a)=10-14,δ0=1 mm;(b)=10-14m-2/3,σ0=4 cm;(c)=10-14m-2/3,β=30;(d)σ0=4 cm,β=40
[1]Shirai T,Wolf E 2002 Opt.Commun.20425
[2]Deschamps J,Courjon D,Bulabois J 1983 J.Opt.Soc.Am.73256
[3]Jian W 1990 J.Mod.Opt.37671
[4]Gase R 1991 J.Mod.Opt.381107
[5]Andrews L C 2005 Laser Beam Propagation through Random Media(Washington:SPIE)p67,pp500–510
[6]Clifford S E,Gracheva M E,Ishimaru A 1978 Laser Beam Propagation in the Atmosphere(New York:Springer)pp129–168
[7]Andrews L C 2001 Laser Beam Scintillation with Applications(Washington:SPIE)pp1–60
[8]Collett E,Wolf E 1978 Opt.Lett.227
[9]Friberg A T,Sudol R J 1983 Opt.Acta:Int.J.Opt.301075
[10]Salem M,Korotkova O,Dogariu A,Wolf E 2004 Waves in Random Media 14513
[11]Korotkova O,Salem M,Wolf E 2004 Opt.Commun.233225
[12]Cheng K,Lü B D 2009 Acta Phys.Sin.58250(in Chinese)[程科,呂百達2009物理學報58250]
[13]Ji X L,Li X Q 2009 Acta Phys.Sin.584624(in Chinese)[季小玲,李曉慶2009物理學報584624]
[14]Lü S Y,Lü B D 2009 Chin.Phys.B 183883
[15]Wu J,Boardman A D 1991 J.Mod.Opt.381355
[16]Mandel L,Wolf E 1995 Optical Coherence and Quantum Optics(Cambridge:Cambridge University Press)p279
[17]Roychowdhury H,Ponomarenko S A,Wolf E 2005 J.Mod.Opt.521611
[18]Lü B D 2003 Laser Optics:Beam Characterization,Propagation and Transformation,Resonator Technology and Physics(Beijing:Higher Education Press)p203(in Chinese)[呂百達2003激光光學:光束描述,傳輸變換與光腔技術物理(北京:高等教育出版社)第203頁]
[19]Born M,Wolf E 2005 Principles of Optics(Cambridge:Cambridge University Press)p564
[20]Collett E,Wolf E 1980 Opt.Commun.3227
[21]Foley J T,Zubairy M S 1978 Opt.Commun.26297

