廣義信息集博弈Nash平衡的本質(zhì)連通區(qū)

孫修勇

（ 凱里學(xué)院 數(shù)學(xué)科學(xué)學(xué)院，貴州 凱里 556011 ）

1．引言

近年來，博弈論的研究及應(yīng)用非常活躍，一直是學(xué)界關(guān)注的焦點(diǎn)。從1994年諾貝爾經(jīng)濟(jì)學(xué)獎(jiǎng)授予三位博弈論專家至今，一共有六屆諾貝爾經(jīng)濟(jì)學(xué)獎(jiǎng)與博弈論的研究有關(guān)。一方面,博弈論在不斷地拓展其應(yīng)用領(lǐng)域,另一方，面博弈論的研究者們正致力于解決博弈理論本身不斷出現(xiàn)的嚴(yán)峻問題。

Nash平衡是非合作博弈理論的核心概念。每一局中人如何通過個(gè)人的理性預(yù)測(cè)到共同的平衡點(diǎn)，是實(shí)際問題中Nash平衡能否真正產(chǎn)生的關(guān)鍵。近年來，Nash平衡的多重性成為博弈論本身，及其應(yīng)用研究中最為棘手的問題。作為以解釋實(shí)際現(xiàn)象和解決現(xiàn)實(shí)問題為己任的重要理論，博弈論面臨的最大困惑是：平衡點(diǎn)不止一個(gè)，甚至有無窮多個(gè)。在實(shí)際問題中，不同的局中人如何通過個(gè)人的理性一致地預(yù)期到同一個(gè)平衡點(diǎn)？也就是說，平衡能否真正意義上實(shí)現(xiàn)？

多個(gè)Nash平衡帶來的這一重大缺陷，一直是博弈論研究者關(guān)注的焦點(diǎn)。從20世紀(jì)60年代開始，尋求改進(jìn)和精煉Nash平衡的機(jī)制和方法一直是博弈論研究最活躍的領(lǐng)域。這其中包括了1994 年Selten和 Harsanyi獲得諾貝爾獎(jiǎng)的成果---“子博弈精煉Nash平衡”、“顫抖的手的均衡”和“貝葉斯Nash平衡”等，也包括2007年度諾貝爾經(jīng)濟(jì)學(xué)獎(jiǎng)獲得者M(jìn)yerson提出的“恰當(dāng)平衡”，Kreps和Wilson提出的“序貫平衡”等精煉Nash平衡的概念。[1]2005年度諾貝爾經(jīng)濟(jì)學(xué)獎(jiǎng)獲得者Aumann和Schelling也曾分別提出過“強(qiáng)均衡”和“聚點(diǎn)均衡”的概念。

圍繞平衡的精煉，1986年Kohlberg與Mertens[2]建立的KM平衡概念（即策略穩(wěn)定集（Strategic Stable Set））是Nash平衡精煉的標(biāo)志性成果。KM平衡可以歸結(jié)為穩(wěn)定性的方法，即策略集擾動(dòng)（顫抖）意義下Nash平衡點(diǎn)集的極小本質(zhì)集。KM平衡之所以成為Nash平衡選擇和精煉的一個(gè)重要里程碑，是因?yàn)樗偨Y(jié)了眾多精煉Nash平衡的概念，并由此提出公理化的框架。令人遺憾的是，Kohlberg和Mertens提出的穩(wěn)定集無法完全滿足他們所給出的KM條件。之后，Mertens、Hillas等人曾經(jīng)圍繞穩(wěn)定集的概念作過一些修正和改進(jìn)[3-6]，甚至加上了拓?fù)渫瑐惖纫恍?shí)際意義不十分明朗的數(shù)學(xué)化條件。因?yàn)槠胶獾亩嘀匦允遣┺恼摬坏貌徽暤娜毕荩瑖@平衡的選擇和精煉，新的結(jié)果在不斷地涌現(xiàn)[7-15]，但多重 Nash平衡所帶來的問題始終未能得到很好的解決。

針對(duì)Nash平衡的多重性，尋求一種普遍認(rèn)可的機(jī)制，尤其是實(shí)際意義較為明朗的精煉機(jī)制（不完全是純數(shù)學(xué)意義的），是決定博弈理論能否更加合理地解釋實(shí)際問題的關(guān)鍵。本文將通過對(duì)廣義信息集的方法研究Nash平衡的本質(zhì)連通區(qū)問題。

2．預(yù)備知識(shí)

局中人的策略集：對(duì)于每一iN∈，非空集合iX為局中人i的策略集，記

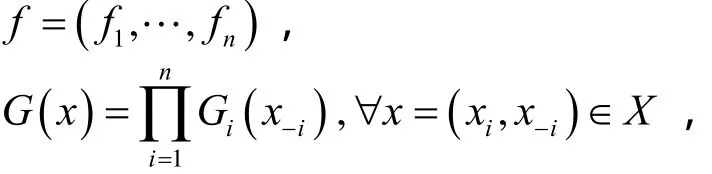
也可將此廣義博弈簡記為ΓG= N;X;G;f 。

則稱*x為廣義博弈GΓ的Nash平衡點(diǎn)。

3．廣義博弈Nash平衡的本質(zhì)連通區(qū)

（ⅰ）對(duì)于每一iN∈，iX為線性拓?fù)淇臻g中緊凸子集；

（ⅱ）對(duì)于每一iN∈，if在X上連續(xù)；

則廣義博弈GΓ存在Nash平衡點(diǎn)。

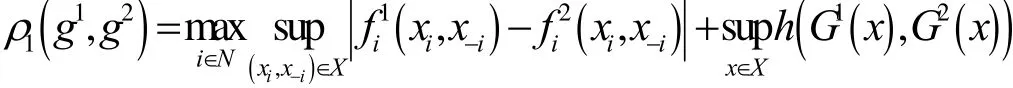
其中h為 K （X）上的Hausdorff度量，則ρ1為M1上的度量。

證明：由Φ關(guān)于一致度量的完備性及1ψ關(guān)于一致Hausdorff度量的完備性即可給出證明。

設(shè)廣義博弈

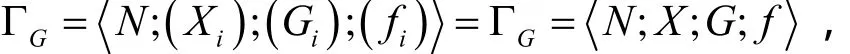
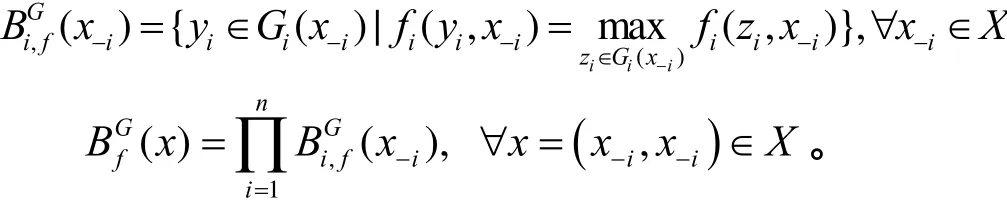
由上述定義，不難驗(yàn)證下面的引理。

引理 2*xX∈為廣義信息博弈的Nash平衡點(diǎn)當(dāng)且僅當(dāng) x*為最優(yōu)反應(yīng)映射的不動(dòng)點(diǎn)。

定理2 設(shè)廣義博弈

關(guān)于M的強(qiáng)本質(zhì)連通區(qū)，設(shè)為 c（f, IG,θ）。于是，對(duì)任意的0ε﹥，存在0δ﹥，使得對(duì)于所有滿足）的，有

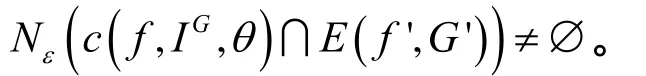
[1]D．Fudenberg，J．Tirole， Game Theory， MIT Press， 1998．

[2]E． Kohlberg and J. F. Mertens, On the strategic stability of equilibria，Econometrica，54 （1986），1003-1037．

[3]J．F．Mertens，Stable equilibria-A reformulation，Part I：Definition and Basic Properties, Mathematics of Operations Research，14（1989）， 575-625．

[4]J．F．Mertens，Stable Equilibria - A Reformulation，Part II：Discussion of the Definition and Further Results.Mathematics of Operations Research，16（1991），694-753．

[5]J．F，Mertens，Ordinality in non cooperative games，International Journal of Game Theory，32（2003），387-430．

[6]J．Hillas，On the definition of the strategic stability of equilibria，Econometrica，58（1990）， 1365-1390．

[7]J．Hillas，M．Jansen，J．Potters and D．Vermeulen，On the Relation Among Some Definitions of Strategic Stability，Mathematics of Operations Research，26：3（2002）．

[8]E．Van Damme，Strategic Equilibrium，in R. Aumann and S．Hart （eds．） HANDBOOK OF GAME THEORY，Vol．3，Chapter 41，Amsterdam：Elsevier，2002．

[9]S．Govindan and J．F．Mertens，An equivalent definition of stable equilibria，Intenational Journal of Game Theory，32（2003），339-357．

[10]S．Govindan and R．Wilson，Maximal Stable Sets of Two-Player Games，International Journal of Game Theory，30：4（2001），557-566．

[11]S．Govindan and R．Wilson， Axiomatic Justification of Stable Equilibria， Econometrica．

[12]S．Govindan and R．Wilson, Characterization of Hyperstability， Econometrica．

[13]J．Yu．Essential quilibria for n-person Noncooperative Games，Journal of Mathematical Economics，1999，31：361-372．

[14]Yu，S．W．Xiang，On essential component of the set of Nash equilibrium points，Nonlinear Analysis，1999，38：259-264．

[15]S．W．Xiang，Gui-dong Liu and Yong-hui Zhou．On the strongly essential components of Nash equilibria of infinite n-person games with quasiconcave payoffs，Nonlinear Analysis，2005，63：e2639- e2647．