多區域N體問題解析函數的近似計算
劉 超,章社生, 吳永紅 (武漢理工大學理學院,湖北 武漢 430063)
多區域N體問題解析函數的近似計算
劉 超,章社生, 吳永紅 (武漢理工大學理學院,湖北 武漢 430063)
研究了粒子相互作用的多區域N體問題解析函數的近似計算,利用多重積分和delta函數,求得徑向分布函數的解析表達式,推導出雙球域的分析解。計算結果表明,當粒子數為2000個時,計算誤差小于千分之一,且計算速度快。
粒子模擬;N體問題;徑向分布函數;多重積分;分析解;數值解
粒子模擬已經成為車路協同等科學領域的重要研究工具[1],它將復雜系統(生物大分子、星系、車路協同等)看成是大量經典物理可描述的單個個體(原子、星體等 )的集合,然后對所有這些個體特征數據進行分析。筆者專注于一種在粒子模擬數據分析中占有極其重要地位的雙體關聯函數查詢-空間距離直方圖(SDH)的研究[2],并且關注Barnes2Hut算法(BHA)和快速多極子方法( FMM)[3]。SDH是一種被稱為徑向分布函數(RDF)的連續統計分布函數的直接估計[4-5],與該系統的結構因子(structure factor)相關聯[6]。當研究區域為單連通時,文獻[7]求出了粒子相互作用徑向分布函數的解析表達式,該工作能推廣到互不相連的多區域N體問題。
1 多區域粒子徑向分布
徑向分布函數(RDF)[7]的定義為:
(1)
式中,Fh(r)是在粒子之間距離為r,厚度為h的球殼內粒子距離數量,稱為距離和函數。設粒子坐標為Xi,i=1,…,N,則距離和函數Fh(r)可表示為:
(2)
式中,r*=|Xi-Xj|為Xi與Xj之間的距離;當|r*-r|≤h/2時函數δh=1,當|r*-r|>h/2時函數δh=0。式(2)中除以2是為了消去重復累加。
用一個立方體Ω包含所有粒子。按粒子分布的稀疏情況,將立方體Ω劃分為N′個子區域Ωk(k=1,…,N′),則距離和函數Fh(r)可表示為:
(3)
式中,Fi,j為第i個區域中的粒子與第j個區域中的粒子之間的距離和函數;當j=i時表示第i個區域內部粒子之間的距離和函數,當j≠i時表示第i個區域中的粒子與第j個區域中的粒子之間的距離和函數。
2 雙球域分析解
考慮粒子分布在2個球域O和O′,球內分別有N和N′個粒子,對應粒子密度分別為ρ和ρ′(粒子數除球體積),兩球心距離為a,半徑分別為R和R′。取粒子距離和函數為:
Fh(r)=F11(r)+F12(r)+F22(r)
(4)
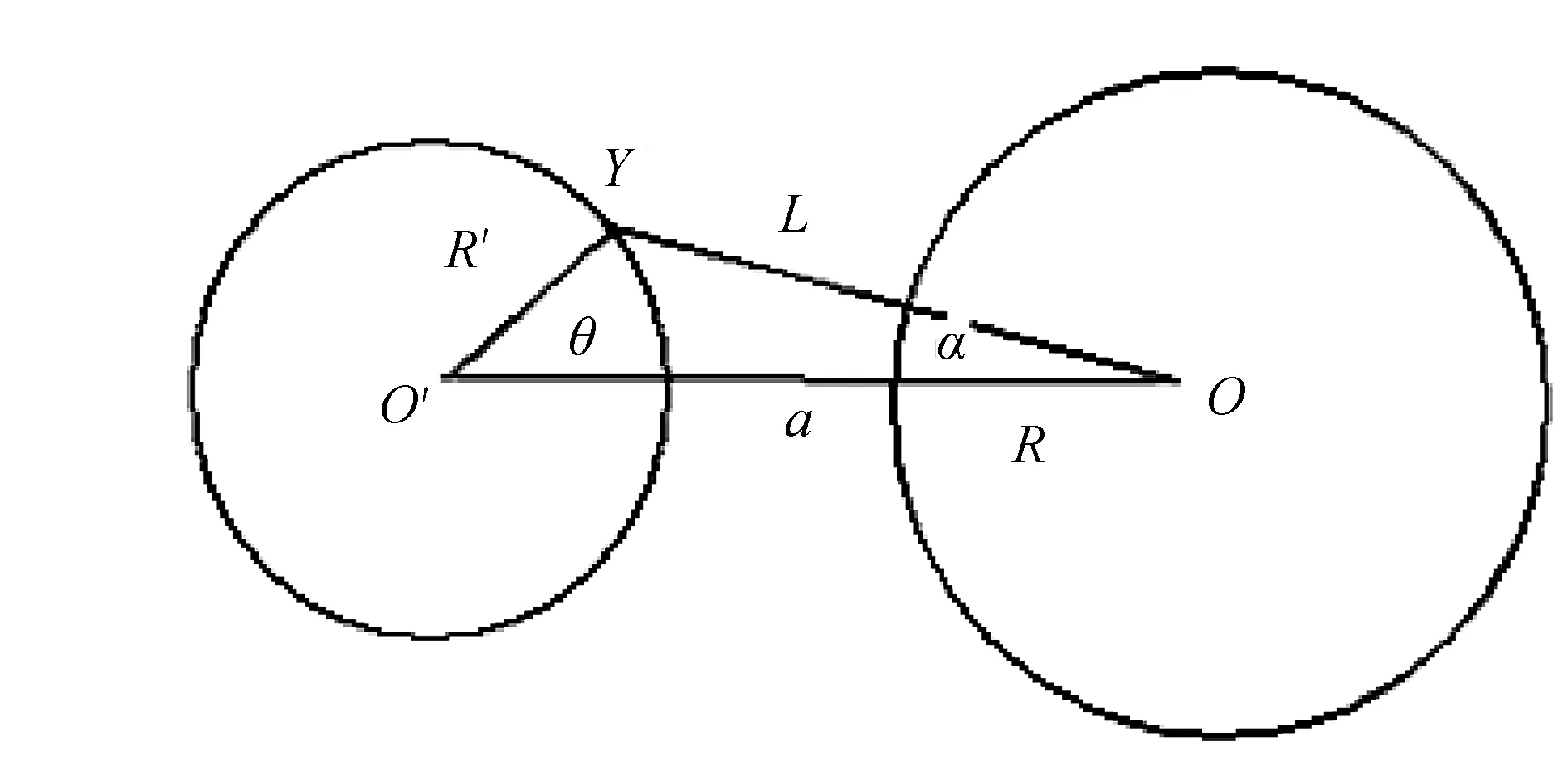
圖1 雙球域對數示意圖
式中,r=mh,h為步長,m=1,2,3,…;F11(r)為球O內部粒子產生的距離和函數;F22(r)為球O′內部粒子產生的距離和函數;F12(r)為球O中的粒與球O′中的粒子相互作用產生的距離和函數;F11(r)和F22(r)用文獻[7]中的公式計算。設點Y為球O′表面點,它到點O的距離為L(見圖1),則點Y與球O中粒子距離和函數為:

(5)
根據空間距離直方圖(SDH)的定義[2],將球域O劃分為M′個子區域dΩ,第i個子區域dΩi內的粒子數為n(i),子區域的中點坐標為Yi,第i個子區域中點和區域外點Y的距離為|Yi-Y|,用n(i)|Yi-Y|近似表示第i個子區域內所有粒子與在Y點粒子的距離的和。將下標i從1取到M′,然后求和, 再根據多維積分的定義,當dV非常小時,有:
Y(r)=0r
(6)
式(6)只與距離L和R有關,與粒子坐標Y無關。容易求得,球心在O點,半徑為L的球與球O′的中粒子相互距離為r的距離函數:
(7)
式中:
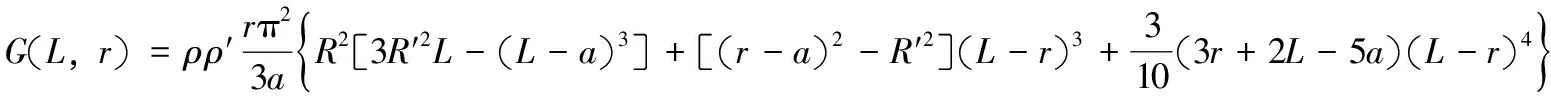
3 算例及誤差分析
例1設2球半徑R=R′=1,球心相距a=3, 每個球內隨機均勻分布M個粒子,研究粒子的分布。
例1中2球之間的距離大于球的半徑,它們能放置于半徑為2.5的大球中,但用半徑為2.5的大球的粒子徑向分布解析公式計算將帶來較大的誤差。下面筆者用雙球粒子徑向分布解析公式計算。
由于半徑R=1, 則有:
(8)
且:
此時,只有2種情況:①r≤a,(L1,L2)=(a-1,r+1); ②r>a;(L1,L2)=(r-1,a+1)。
取粒子數M=500,半徑R=R′=1,兩球心距離a=3,步長h=0.1;球中粒子點用隨機方法產生。對應的計算值繪于圖2。圖2中實線為理論值,星號為直接計算值(用2點之間距離公式計算)。圖2中有2個峰值,第1個峰在r=1附近,由球內粒子相互作用產生。第2個峰值在r=3, 它由球與球中的粒子相互作用產生。由圖2可知,當粒子僅為M=500時,理論解與直接法計算結果接近。進一步計算表明,當球中粒子數增加時,能減少理論計算誤差。
定義平均誤差為Er:
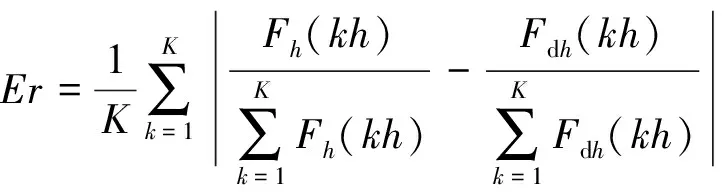
(9)
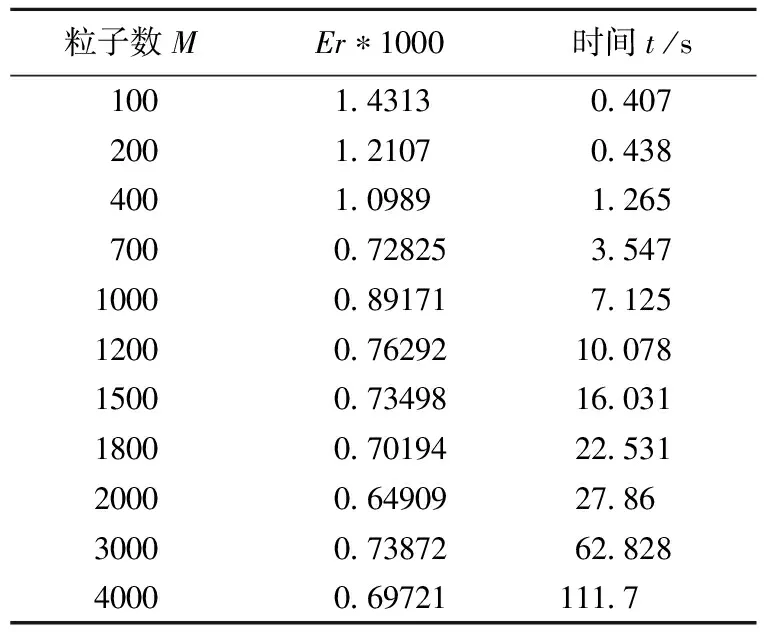
表1 平均誤差Er和直接法CPU計算時間t隨粒子數M的變化
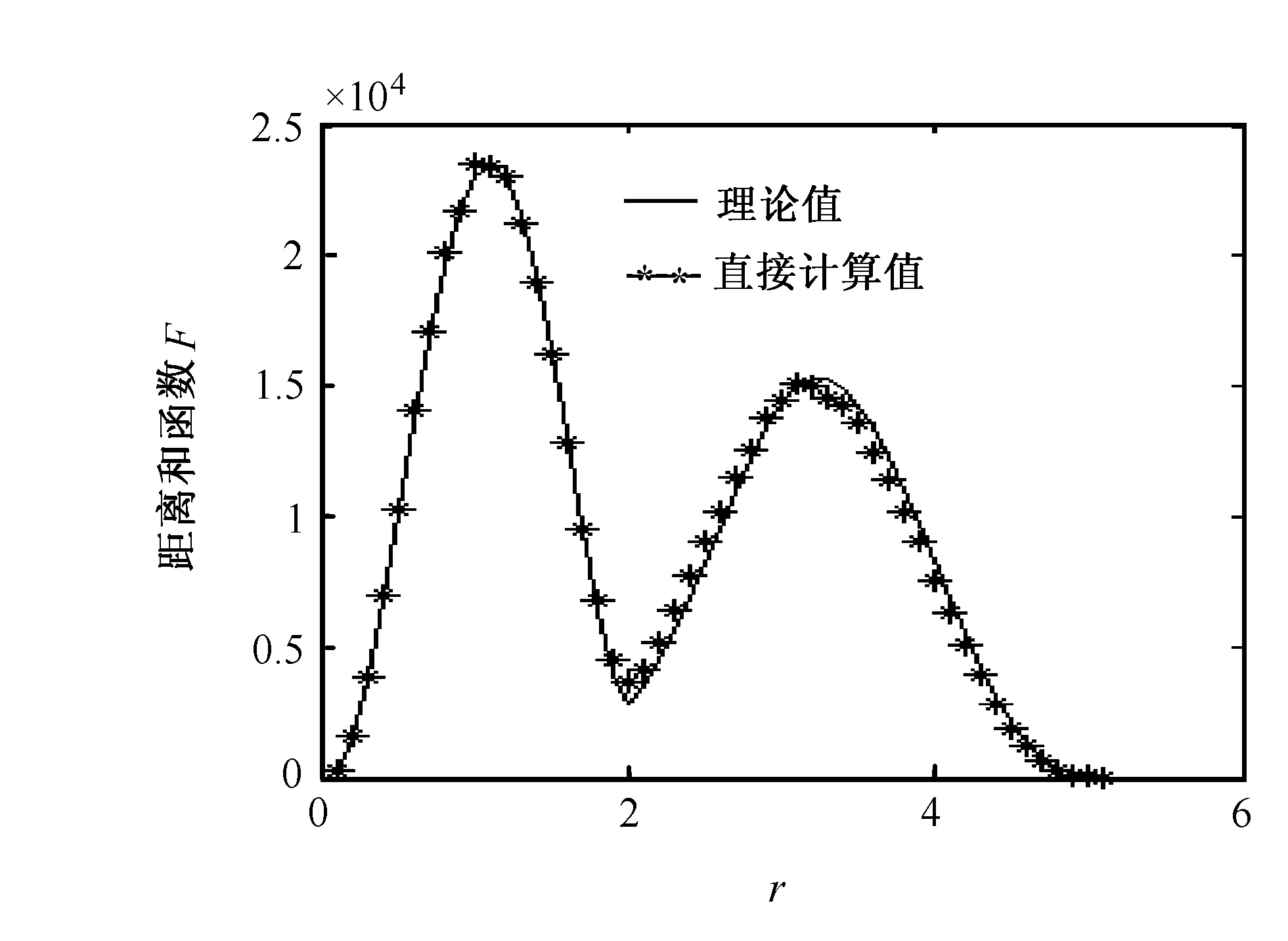
圖2 2球距離和函數隨r的變化
當R=1、R′=1、a=3、h=0.1時,平均誤差Er和CPU計算時間t如表1所示。表1中M為球內粒子數,計算平均誤差Er乘了1000,計算時間t為直接法的CPU計算時間。由表1可知,當粒子數M=100時,平均誤差小于2‰,粒子數增加后,平均誤差總體上減少,但發現有波動。原因是粒子坐標點是用隨機方法選取的,當粒子總數M改變后,粒子坐標都改變。由表1可知,隨著粒子數增加,CPU計算時間增加很快。
4 結 語
筆者推廣了已有的理論[7],構造了多區域解析計算模型,得到了近似計算徑向距離的積分表達式。在粒子密度為均勻分布的條件下,得到雙球域積分解。實例計算結果表明,積分解有很高的精確度,且計算速度快。
[1]胡旻,祝大軍,劉大剛,等.粒子模擬軟件吸收邊界的研究[J].強激光與粒子束,2006,18(8):1315-1318.
[2] Tu Yi-cheng, Chen Shao-ping, Sagar Pandit.Computing Distance Histograms Efficiently in Scientific Databases[A].In procedings of ICDE[C]. 2009:796-807.
[3]王武,馮仰德,遲學斌.樹結構在N體問題中的應用[J].計算應用研究,2008,125(1):42-44.
[4] Bamdad M, Alavi S, Najafi B,et al.A new expression for radial distribution function and infinite shear modulus of Lennard Jones fluids [J].Chem Phys, 2006, 325:554-562.
[5]陳念貽,徐馳,李通化.LiF-KCl熔鹽溶液的Monte Carlo法計算機模擬研究-I:徑向分布函數和熱力學性質[J].中國科學(B輯),1987(1): 21-26.
[6] Filipponi A. The radial distribution function probed by X-ray absorption spectroscopy[J].J Phys Condens Matter, 1994,6:8415-8427.
[7] 陳紹平,章社生.N體問題解析函數近似計算[J].數值計算與計算機應用,2011 (2):143-147.
2012-11-16
國家自然科學基金項目(61240048);武漢理工大學ITS開放基金(ERCTSF2013A001)。
劉超(1990-),男,碩士生,現主要從事應用數學方面的研究工作。
吳永紅(1976-),男,博士,講師,現主要從事應用數學方面的教學與研究工作;E-mail:sheshengz@qq.com。
O242.2
A
1673-1409(2013)04-0004-03
[編輯] 洪云飛

