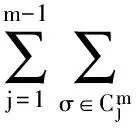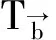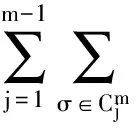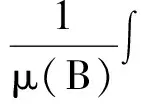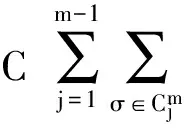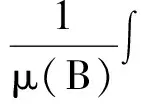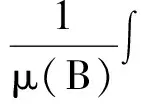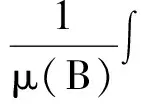多線性交換子的Sharp估計
周檬,許現暉,石建國
(1.河北軟件職業技術學院 信息工程系,河北 保定 071000;2.河北軟件職業技術學院 學生處,河北 保定 071000)
多線性交換子的Sharp估計
周檬1,許現暉1,石建國2
(1.河北軟件職業技術學院 信息工程系,河北 保定 071000;2.河北軟件職業技術學院 學生處,河北 保定 071000)
通過奇異積分算子的有界性,利用函數空間的分解和一些基本不等式證明了奇異積分算子構成的多線性交換子在齊型空間的Sharp函數不等式.
多線性交換子;奇異積分算子;齊型空間;BMO空間;Sharp不等式
隨著奇異積分算子的發展,與其構成的交換子也得到了很好的研究[1-4],令b∈BMO(Rn),T為Caldero′n-Zygmund算子.由b和T生成的交換子[b,T]定義為
[b,T]f(x)=b(x)Tf(x)-T(bf)(x).
Coifman等[5]證明了一個經典結論即交換子[b,T]是Lp(Rn)有界的,當1 首先,介紹一些記號和定義[2,5-6].給定一個集合X,一個函數d:X×X→R+叫做X上的擬距離.如果滿足以下條件: Ⅰ)對X中的x和y,d(x,y)≥0和d(x,y)=0當且僅當x=y. Ⅱ)對X中的x和y,d(x,y)=d(y,x). Ⅲ)存在一個常數l≥1使得d(x,y)≤l(d(x,z)+d(z,y)), (1) 對X中的每一個x,y和z均成立. 令μ為X的子集σ-代數上的正測度,集合X包含半徑為r的球B(x,r)={y:d(x,y) 0<μ(B(x,2r))≤Aμ(B(x,r))<∞, (2) 對所有x∈X和r>0均成立. 上述結構(X,d,μ)叫做齊型空間,其中d和μ如上所述.在式(1)和式(2)中的常數l,A叫做空間常數. b屬于BMO(X),如果b#屬于L∞(X)并且定義‖b‖BMO=‖b#‖L∞.因為‖b-b2kB‖BMO≤Ck‖b‖BMO. 本文主要研究的多線性交換子如下. 定義假設bj(j=1,2,…,m)是X上的固定的局部可積函數,令T為奇異積分算子,即 其中K是在X×X/{(x,y):x=y}的局部可積函數且滿足下列條件: 當d(x,y)≥2d(y,y′),且δ∈(0,1]. 引理1[6]令1 引理2 令1 (b1(x)-(b1)2B)…(bm(x)-(bm)2B)T(f)(x)+(-1)mT((b1-(b1)2B)… |b1(x)-(b1)2B)…(bm(x)-(bm)2B)T(f)(x)|+ |T((b1-(b1)2B)…(bm-(bm)2B)f2)(x)-T((b1-(b1)2B)…(bm-(bm)2B)f2)(x0)|= I1(x)+I2(x)+I3(x)+I4(x). 對于I1(x),根據H?lder不等式,1/p1+1/p2+…+1/pm+1/t=1,其中1 對于I2(x),根據Minkowski不等式和H?lder不等式,有 對于I3(x),選取1 對于I4(x),取1 證畢. [1]ALVAREZJ,BABGYR,KURTZD,etal.Weightedestimatesforcommutatorsoflinearoperators[J].StudiaMath, 1993(104):195-209. [2]PEREZC.Endpointestimateforcommutatorsofsingularintegraloperators[J].FuncAnal, 1995, 128: 163-185. [3]PEREZC,PRADOLINIG.Sharpweightedendpointestimatesforcommutatorsofsingularintegraloperators[J],MichiganMath, 2001, 49:23-37. [4]石建國,周檬,楊景發,等.多線性奇異積分算子構成的交換子在Hardy空間的有界性[J].河北大學學報:自然科學版,2011,31(2):126-129. SHIJianguo,ZHOUMeng,YANGJingfa,etal.BoundednessformultilinearcommutatorofsingularintegralinHardyonspacesofHomogeneoustype[J].JournalofHebeiUniversity:NaturalScienceEdition, 2011, 31(2):126-129. [5]PEREZC,TRUJILLO-GONZALEZR.Sharpweightedestimtesformultilinearcommutators[J].JLondonMathSoc, 2002,65:672-692. [6]COIFMANR,ROCHBERGR,WEISSG.FactorizationtheoremsforHardyspacesinseveralvariables[J].AnnofMath, 1976, 103:611-635. [7]ABERNARDISA,HARTZSTEINS,PRADOLINIG.Weightedinequalitiesforcommutatorsoffractionalintegralsonspacesofhomogeneoustype[J].JMathAnalAppl, 2006, 322:825-846. Sharpestimateformultilinearcommutator ZHOUMeng1,XUXianhui1,SHIJianguo2 (1.Information Engineering, Hebei Software Institute, Baoding 071000, China; 2.Student Affairs Office, Hebei Software Institute, Baoding 071000, China) The sharp function inequality for the multilinear commutator related to the singular integral operator on the space of homogeneous type by means of the boundedness of singular operator was proved.The main tools of the proof were decomposition of function spaces and some general inequalities. multilinear commutator; singular integral; space of homogeneous type; BMO space; Sharp inequality 10.3969/j.issn.1000-1565.2013.01.003 2011-12-25 河北省科學技術研究與發展計劃項目(11227167) 周檬(1980-),女,河北保定人,河北軟件職業技術學院講師,主要從事積分算子方向的研究. E-mail:zm_000@126.com O174.3 A 1000-1565(2013)01-0010-04 MSC2010: 42B20; 42B25 (責任編輯王蘭英)1 預備知識
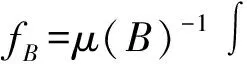
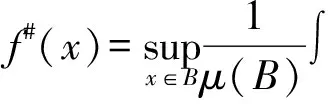
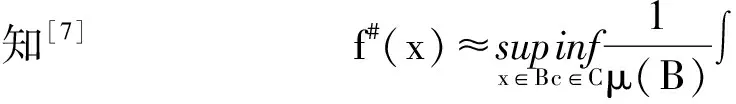
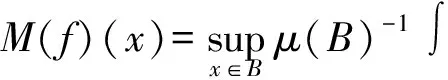
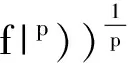

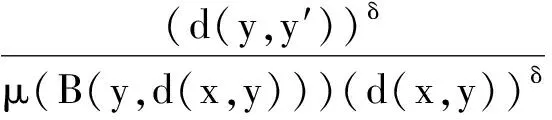
2 主要定理證明