行星齒輪傳動中滾子軸承的壽命計算模型

譚 昕

（江漢大學 機電與建筑工程學院，湖北 武漢430056）

滾子軸承在風力發電機增速箱（以下簡稱增速箱）中大量使用，同時也是增速箱中故障率最高的零部件。據統計，風力發電系統故障70%來源于軸承失效，尤其是行星架前端、后端軸承的故障率約占軸承失效的90%［1］，其主要失效形式是點蝕和膠合。因此，有效、快速預測增速箱中軸承的使用壽命是一個重要的課題。

本文首先運用Lundberg－Palmgren方法建立滾子軸承的準動力學方程，計算滾動體的滑動率及內、外圈滾道的載荷分布；然后，建立增速箱系統的多體動力學模型，通過對動態行為的分析計算軸承的預期壽命及相關參數，并將兩種計算結果進行了對比。

1 軸承準動力學方程的建模與計算

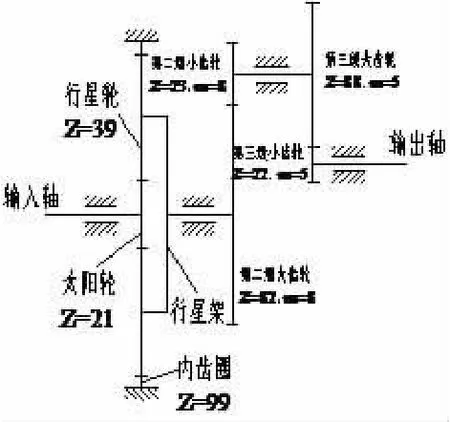
圖1 增速箱的傳動原理簡圖

圖1是某型1.5兆瓦風力發電機增速箱傳動鏈簡圖。本文的研究對象是該齒輪箱中行星架上風端（即前端）軸承的壽命。增速箱的主要傳動參數如表1所示。

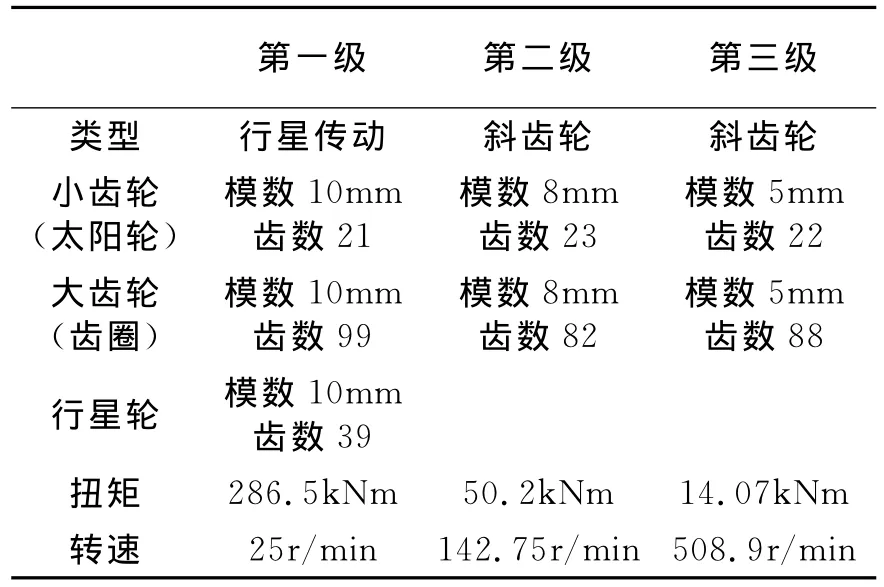
____________表1 增速箱主要傳動參數

假設軸承受到葉輪的軸向力為Fa，軸承的徑向載荷用Fr表示，圍繞軸向的傾覆力矩用Mr表示，則軸承滾動體所承受的最大載荷為：

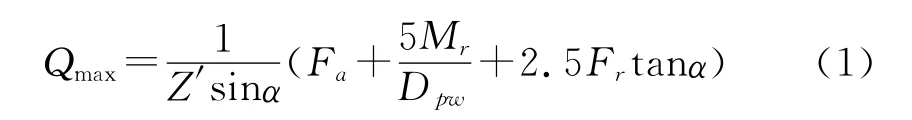
式（1）中：Qmax為所有滾動體中的最大載荷，Dpw為滾動體所在的節圓直徑，α為軸承內、外圈之間的軸向偏轉角；Z′為在某個方向上承受軸向力的滾動體數目。

根據 Lundberg－Palmgren理論［2］，軸承滾動體所受載荷的分布情況計算流程如下：

1）首先計算軸承滾動體在軸向外載荷和內、外圈傾覆力矩聯合作用下所承受的復合載荷；

2）計算軸承滾動體在徑向載荷單獨作用下所承受的載荷；

3）將上述兩個計算結果進行聯立求解，獲得其矢量和即為整個滾動體的載荷分布。

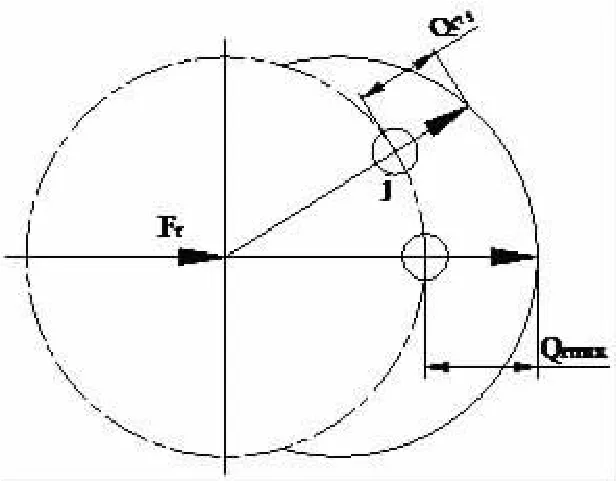
圖2 軸承滾動體的接觸載荷計算模型

如圖2所示，根據彈性接觸力學理論［3］，在傾覆力矩和軸向載荷復合作用下第j個滾動體的接觸載荷為：

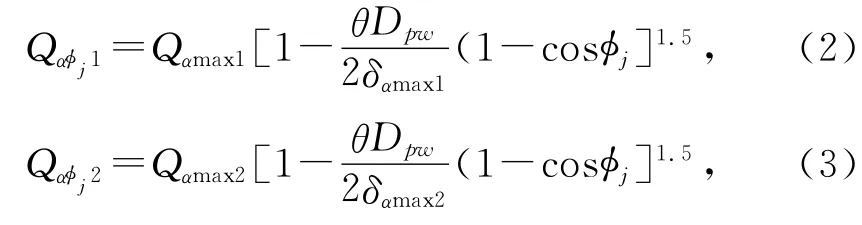
式中：Qαmax1、Qαmax2為滾動體在軸向承受的最大載荷；φj為滾動體位置角；θ 為軸承傾斜角；δαmax1、δαmax2為滾動體的最大軸向變形；j＝1，2，…，Z′；若軸向力作用方向為正，Qαmax1、Qαφj1和δαmax1為正；Qαmax2、Qαφj2和δαmax2為正。

當Fα＝0，Mr＝0時，Qrmax＝Qmax，則滾動體的徑向載荷分布可由下式計算：

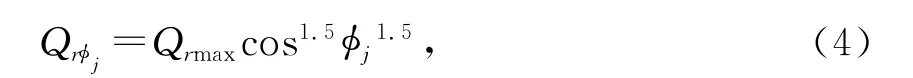
上式中：Qrmax為滾動體所承受的最大徑向載荷；Qrφj為第j個滾動體所受到的徑向載荷。

本文根據Lundberg－Palmgren理論及其計算步驟在Matlab環境下編程，以行星架前端軸承為例進行計算。行星架前端軸承采用SKF 230／530CA／W33雙排調心圓柱滾子軸承，軸承材料為G20Cr2Ni4，彈性模量為206GPa，泊松比0.3，許用接觸應力650MPa，受力計算結果如表2所示。

表2 行星架前端軸承受力計算結果

軸承的12個滾動體位載荷分布如圖3所示。

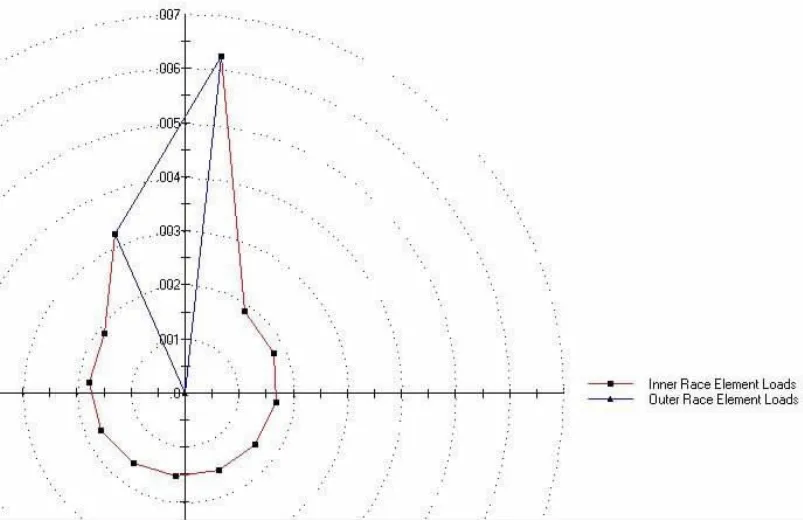
圖3 軸承滾動體載荷分布

從圖3可以看出，軸承的第一和第十二滾動體位載荷最大，分別達到1.46GPa和1.17GPa，這只是名義載荷，而實際載荷譜的峰值可以達到名義載荷的3倍以上，并且反轉的最大載荷值也可以達到名義載荷的2倍以上。在實際載荷遠大于名義載荷的情況下，軸承內外圈滾道出現應力集中的概率會大幅提高，這種現象尤其容易出現在第一級行星架上。因為第一級行星架采用雙壁式中空結構，其結構剛度較差，同時承受的扭矩載荷較大，因此本身容易出現偏心的情況，從而導致軸承產生位錯，加劇應力集中的發生。圖4是同一滾動體在不同滾動體位的載荷分布。

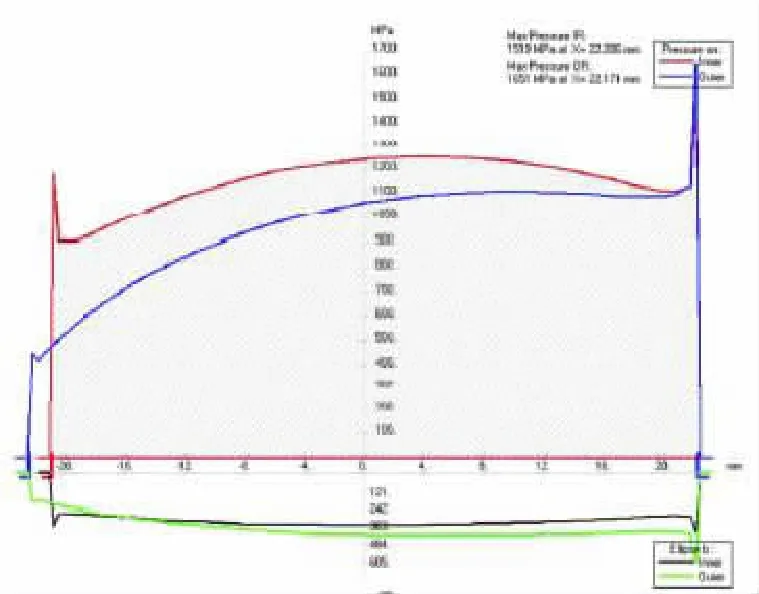
圖4 滾動體在不同位置時的載荷分布

從圖4可以看出，滾動體在第一和第十二滾動體的位置上存在較大的應力集中現象，其應力幅值較一般位置滾動體為大，且變化劇烈。

表3 軸承的計算壽命及當量動載荷

表3所示為軸承的計算壽命、當量動載荷及計算時間。從表3可以看出，軸承的參考壽命為14595小時，約為1.66年。通常風力發電機系統的設計壽命為15年，3年一次大修，因此該軸承沒有達到設計要求。

2 增速箱的虛擬建模與軸承壽命動態仿真計算

為了驗證準動力學方程的計算結果，本文在RomaxWind環境下建立整個增速箱系統的虛擬模型，通過動態仿真來計算軸承的預期壽命。RomaxWind是英國RomaxTech公司出品的一個基于多體動力學的大型數值仿真軟件，其中帶有大量軸承校核函數。

在RomaxWind環境中，可視為剛體的零部件，如軸、齒輪等，可以直接調用相應模塊進行建模；而柔性體零部件，如齒圈、軸承、齒輪箱等，則需要在有限元軟件（如Ansys）中建模并劃分網格后，以IGES文件格式導入RomaxWind。增速箱的虛擬建模結果如圖5所示［4］。

圖5 增速箱的虛擬模型

在RomaxWind環境下對增速箱整機進行動態仿真，然后調用軸承分析函數對軸承滾動體載荷分布進行分析。虛擬模型中選用的軸承仍然是行星架前端軸承，其類型同樣為SKF 230／530CA／W33雙排調心圓柱滾子軸承，技術參數與上文相同。滾動體載荷分布如圖6所示。

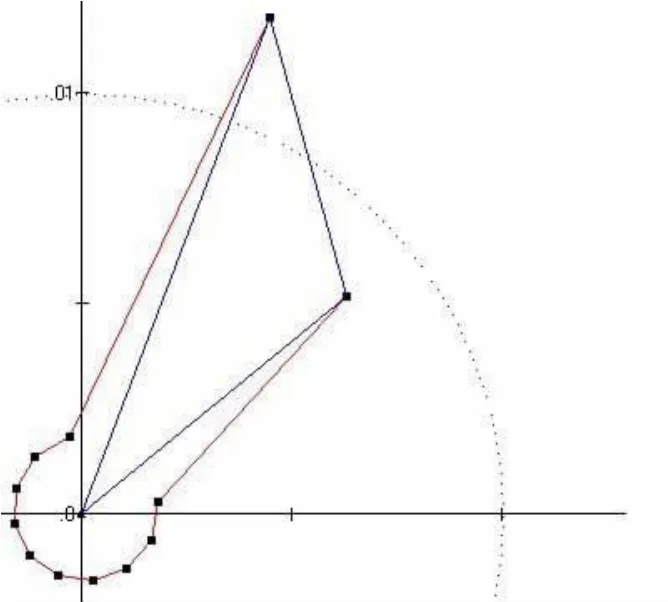
圖6 軸承滾動體載荷分布

從圖6中可以看出，第一和第十二滾動體位載荷仍然最大，分別為1.52GPa和1.13GPa。與圖3相比，不同之處在于第一滾動體位的載荷大于第十二滾動體位。RomaxWind軟件同時提供出軸承內外圈滾道的載荷分布，分別如圖7和圖8所示。

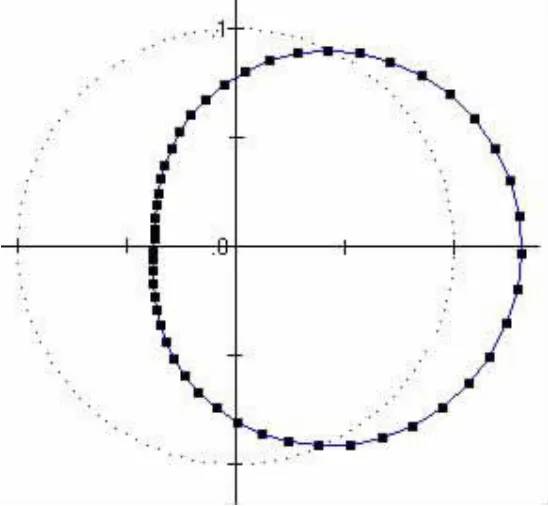
圖7 內圈滾道載荷分布情況

圖7所示為軸承內、外圈之間產生0.15°傾斜時，軸承內圈滾道上載荷分布情況。軸承內、外圈之間的傾斜會導致各滾動體與內、外滾道之間的接觸力與切向拖曳力沿軸向非均勻分布，從而導致滾動體承受沿z軸的傾斜力矩，使滾動體兩端與滾道擋邊間產生接觸力，這種接觸力在外載荷的作用線上為最大，從圖7中可以看出，第二十五滾動體位承受的接觸力為4.3kN。產生這個載荷的主要原因就是風機葉輪在風力偏轉載荷的作用下，軸承內外圈產生較大傾斜，導致接觸力的變大［5］。

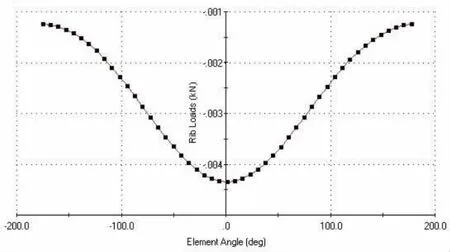
圖8 外圈滾道載荷分布情況

圖8為外圈滾道上載荷分布情況。由于外載荷的下降和主軸轉速的上升，滾子保持架的打滑度會有所上升，產生這一現象的原因是因為軸承內圈對滾動體產生的拖曳力矩下降；另一方面，較大的滾動體產生的離心力又會使軸承外圈對滾動體產生的阻力矩增大；滾動體在剛剛脫離承載區時具有最小打滑度，而滾動體在進入承載區附件后會有最大打滑度。這是因為非承載滾動體只受到外滾道產生的阻力矩。由于滾動體和內、外圈滾道之間必然存在潤滑油膜，所以所有滾子都有打滑現象，仍然需要通過提高軸承滾道及滾子的形狀精度和表面精度來改善潤滑效果。

表4 軸承的計算壽命及當量動載荷

對比表3和表4對應項的數值可知，對于兩種計算模型而言，軸承計算壽命前者比后者小約4%，而軸承當量動載荷前者比后者大5.31%。這說明兩種計算模型的計算結果是吻合的，但軸承準動力學方程所用的計算時間比RomaxWind軟件的時間要少30.66%。

3 結論

本文分別運用軸承準動力學方程模型（集中質量模型）和多體動力學模型（有限元模型）對某型兆瓦級風機齒輪增速箱行星架前端軸承進行了壽命預測和當量動載荷計算，并分析了軸承上載荷分布規律及其對軸承壽命的影響，記錄了計算時間。計算結果表明：

1）風力發電機葉輪的偏轉對行星架前端軸承的壽命有較大影響，是導致軸承燒蝕、膠合失效的主要原因；

2）兩種計算模型獲得了相近的計算結果，偏差不超過6%，但軸承準動力學方程方法具有更快的計算速度，適合大計算量的場合。

［1］王素霞.國內外風力發電的情況及發展趨勢［J］.電力技術經濟，2007，19（1）：29－31.

［2］Kahraman A，Kharazi A A，Umrani M.A deformable body dynamic analysis of planetary gears with thin rims［J］.Journal of Sound and Vibration，2003，262：752－768.

［3］吳林豐，方寧.高速向心滾子軸承準動力學分析［J］.南京航空航天大學學報，1993，25（3）：330－340.

［4］徐亮，楊文濤.RomaxDesigner建模與分析實例［M］.北京：化學工業出版社，2008.

［5］楊威啟.高速輕載圓柱滾子軸承分析［J］.軸承，1999（10）：3－6.