周期信號和關聯噪聲作用下非對稱雙穩(wěn)系統的統計特性研究

王國威，程慶華，徐大海 (長江大學物理科學與技術學院，湖北 荊州 434023

王淑平 (鎮(zhèn)賚第四中學，吉林 鎮(zhèn)賚 137300)

周期信號和關聯噪聲作用下非對稱雙穩(wěn)系統的統計特性研究

王國威，程慶華，徐大海 (長江大學物理科學與技術學院，湖北 荊州 434023

王淑平 (鎮(zhèn)賚第四中學，吉林 鎮(zhèn)賚 137300)

研究了關聯噪聲和周期信號共同驅動下非對稱雙穩(wěn)系統的穩(wěn)態(tài)性質和各階矩。根據劉維方程、諾維科夫原理等方法，得到了系統相應的福克-普朗克方程，并計算了相應的穩(wěn)態(tài)概率分布函數Pst(x)的表達式。定義R=D/Q(其中,D是乘性噪聲強度，Q是加性噪聲強度)，分3種情況(R=1,R>1,R<1)討論了周期信號振幅A和頻率Ω對系統定態(tài)性質和各階矩的影響。結果表明：①當R=1時，Pst(x)隨態(tài)變量x變化的三維圖呈現1條等高的雙峰曲線，且態(tài)變量的各階矩均處于3種情況所對應的3條曲線的最上方；②當R>1時，Pst(x)隨態(tài)變量x變化的三維圖呈現1條左低右高的不對稱雙峰曲線，且態(tài)變量的各階矩均處于3種情況所對應的3條曲線的最下方；③當R<1時，Pst(x)隨態(tài)變量x變化的三維圖呈現1條左低右高的不對稱雙峰曲線，且態(tài)變量的各階矩均處于3種情況所對應的3條曲線的中間位置上。

非對稱雙穩(wěn)系統；穩(wěn)態(tài)；矩；關聯噪聲；郎之萬方程

近年來噪聲對雙穩(wěn)系統的穩(wěn)態(tài)和瞬態(tài)性質的影響一直是人們關注的一個熱點。研究發(fā)現[1]，在某種特定情況下，外部噪聲(乘性噪聲)和內部噪聲(加性噪聲)可能來自同一個噪聲源，并且他們之間彼此關聯。關聯噪聲對非線性系統的動力學研究帶來了很大的影響，并且被應用于很多領域,如生物系統、激光系統、雙穩(wěn)系統等。在關于關聯噪聲和周期信號共同驅動下的雙穩(wěn)系統的穩(wěn)態(tài)性質方面的文獻中，研究對象一般是對稱的雙穩(wěn)系統[2-6]，而對非對稱的雙穩(wěn)系統研究較少，且沒有考慮周期信號的作用。為此，筆者對周期信號對關聯噪聲作用下非對稱雙穩(wěn)系統的定態(tài)性質和矩的影響進行了研究。

1 穩(wěn)態(tài)概率密度函數

關聯噪聲和周期信號共同驅動的非對稱雙穩(wěn)系統[7]，可由以下一維無量綱郎之萬方程給出[8]:

(1)

式中，x為態(tài)變量；t為時間；r為系統非對稱參數；A為周期信號振幅；Ω為信號頻率；ξ(t)和η(t)是具有零均值和非零自相關時間的白噪聲，其統計性質如下[9]:

〈ξ(t)〉=〈η(t)〉=0 〈ξ(t)ξ(t′)〉=2Dδ(t-t′)

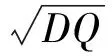
(2)

式中，D和Q分別為乘性噪聲強度和加性噪聲強度；λ為ξ(t)和η(t)之間的關聯系數。

根據文獻[10]，作如下代換：

f(x)=-r+x-x3+AcosΩtg1(x)=xg2(x)=1

(3)

則式(1)可變形為:

(4)

由劉維方程[11]得:

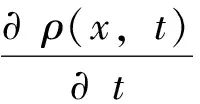
(5)

對式(5)作系綜平均，且由P(x,t)=〈δ(x(t)-x)〉，可得:

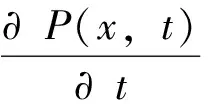
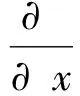
(6)

根據諾維科夫原理[12]:

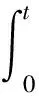
(7)

對式(6)進行整理，得:

(8)

對式(8)進行整理，得:

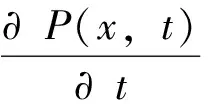
(9)

(10)

(11)

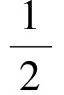
在定態(tài)條件下，式(9)的穩(wěn)態(tài)解為:

(12)

對式(12)積分得穩(wěn)態(tài)概率分布函數:

(13)

態(tài)變量x的各階矩和標準化方差分別為：

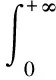
(14)

其中，態(tài)變量x的均值表示式(14)中n=1時的矩。

2 乘性噪聲強度D和加性噪聲強度Q的比率對定態(tài)性質和各階矩的影響

定義R=D/Q，即乘性噪聲強度D和加性噪聲強度Q的比率。根據周期信號和關聯噪聲共同驅動下的非對稱雙穩(wěn)系統的穩(wěn)態(tài)概率分布函數、各階矩和標準化方差的表達式，討論3種情況下(R=1,R<1,R>1)乘性噪聲強度和加性噪聲強度的比率R對系統的定態(tài)性質、各階矩和標準化方差的影響。

2.1R對穩(wěn)態(tài)概率密度分布的影響

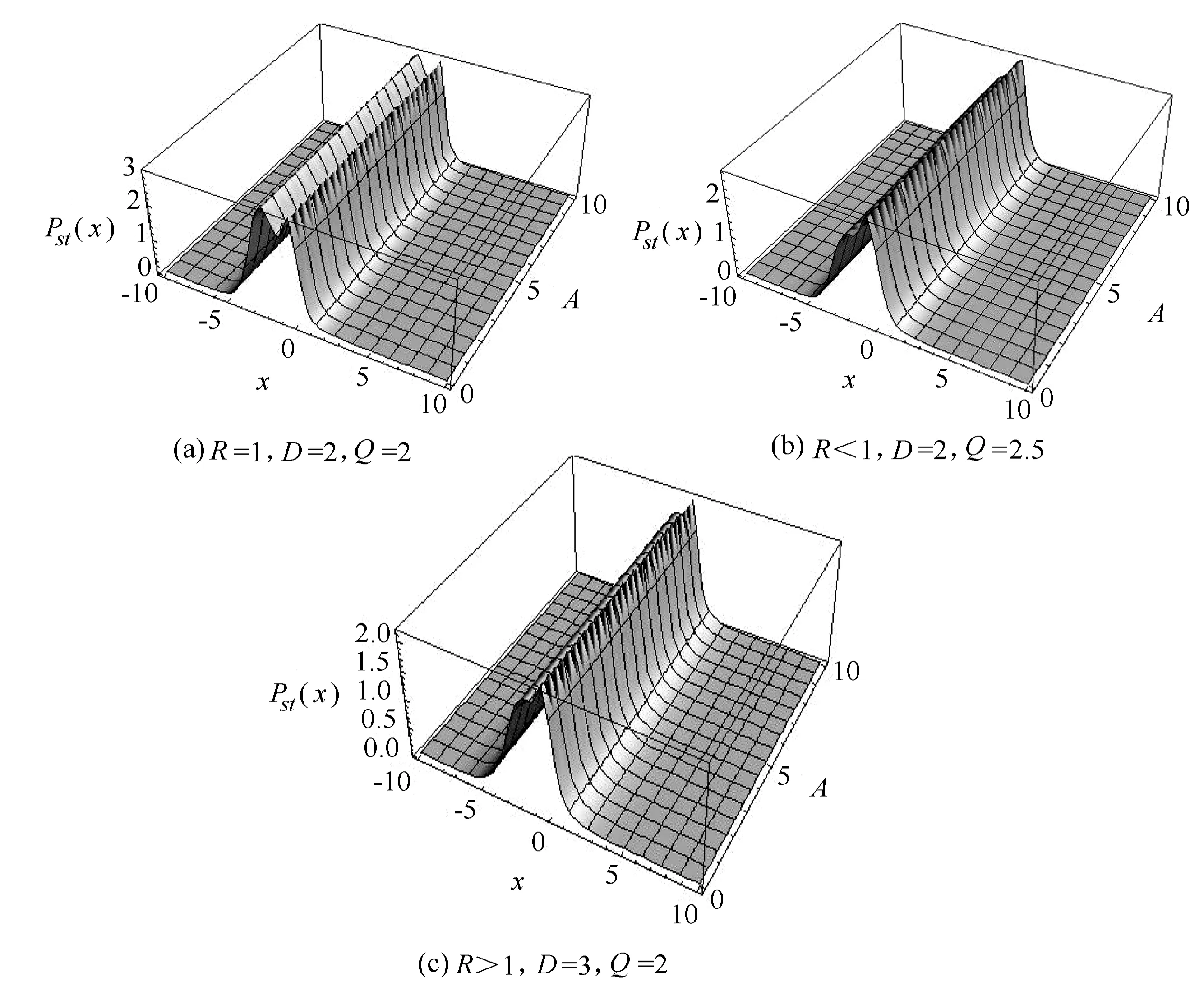
r=7.4;λ=0.6;A=0.5;Ω=1,t=0.01

圖1所示為穩(wěn)態(tài)概率分布函數Pst(x)隨態(tài)變量x和周期信號振幅A在R=1、R>1和R<1時的變化圖。從圖1(a)可以看出，當R=1時，Pst(x)在沿著態(tài)變量x變大的方向上，出現了2個峰值，且左右2個峰值高度基本一致，但左邊的峰比右邊的峰要寬。隨著周期信號振幅A的增加，2峰出現不同的變化，即左邊的峰值高度基本無變化，而右邊的峰值高度出現明顯的波動。從圖1(b)和圖1(c)可以看出，在R<1和R>1的情況下，左邊的峰值高度均變小，2峰均不等高，這和R=1時明顯不同。但是隨著周期信號振幅A的增加，2峰峰值高度均會出現波動。

r=-10;λ=0.6;Ω=10,t=0.01 r=-10,λ=0.6,A=100,t=0.01

r=10;λ=0.6;Ω=100,t=0.01 r=10,λ=0.6,A=100,t=0.01

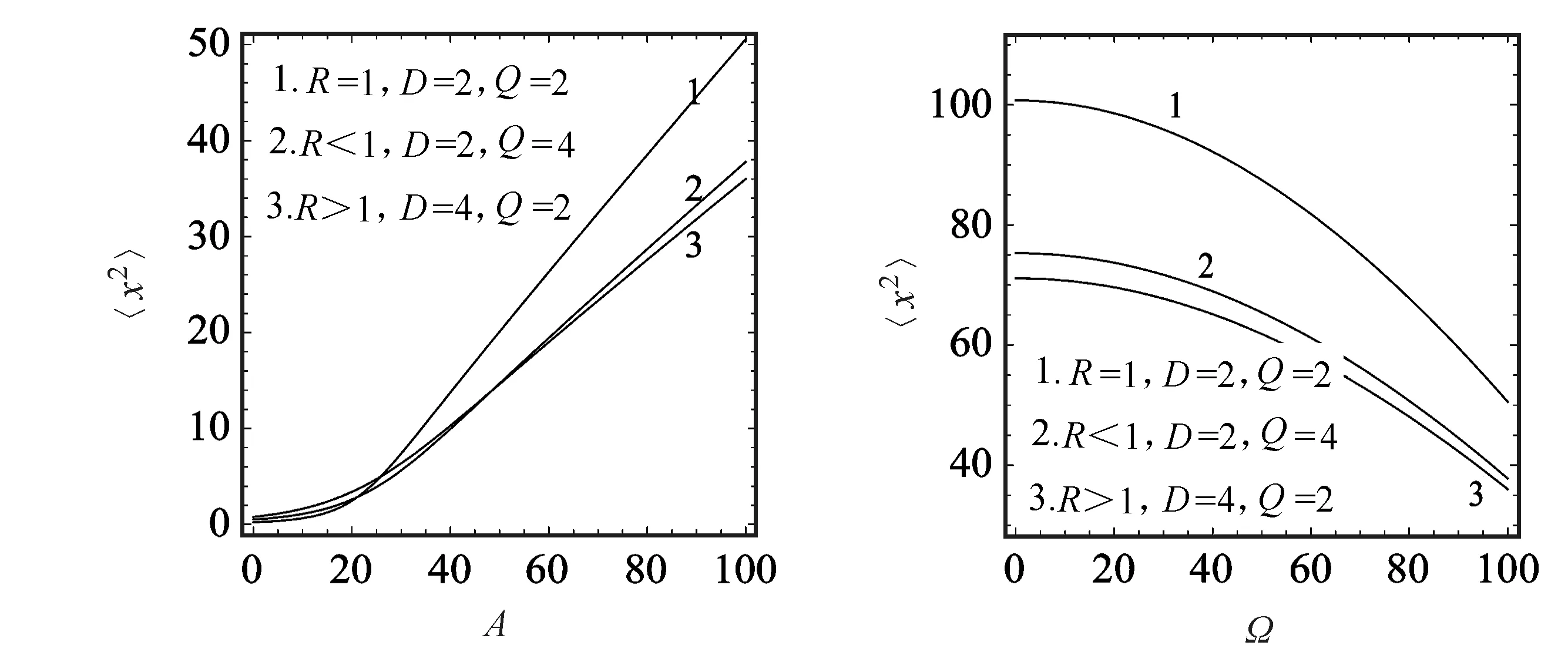
2.2R對一階矩〈x〉的影響

圖2所示為一階矩〈x〉(態(tài)變量均值)作為周期信號振幅A的函數在R=1、R>1和R<1時的變化曲線圖。從圖2可以看出，一階矩〈x〉是周期信號振幅A的單調增函數，且在R=1時，對于輸入系統的某一確定的振幅，其均值大于R<1和R>1時系統的態(tài)變量均值。圖3給出了一階矩〈x〉作為周期信號頻率Ω的函數的變化曲線，從圖3可以看出，一階矩〈x〉隨著周期信號頻率Ω增加而單調減小，而且當周期信號頻率Ω取值較小時，〈x〉隨Ω的增加而減小的趨勢較緩。當Ω的取值大于20時，一階矩〈x〉隨著Ω增加而減小的較快。而且，當R=1時，一階矩〈x〉曲線整體位于R<1和R>1時〈x〉曲線的上方。

2.3R對二階矩〈x2〉的影響

圖4所示為態(tài)變量二階矩〈x2〉隨周期信號振幅A變化曲線圖。從圖4可以看出，當輸入系統信號振幅較小時，增加A的取值對二階矩〈x2〉的影響不明顯，但是當A的取值大于25時，隨著A的增加，二階矩〈x2〉明顯變大，而且在R=1時〈x2〉隨著A的增加而變大的趨勢要比R>1和R<1時要快。圖5所示為二階矩作為周期信號頻率Ω的函數隨R變化曲線圖。從圖5中可以看出，〈x2〉是Ω的單調減函數，且R=1時，二階矩〈x2〉曲線整體位于R>1和R<1時〈x2〉曲線的上方。

r=10;λ=0.6;Ω=100,t=0.01 r=10,λ=0.6,A=100,t=0.01

r=10;λ=0.6;Ω=100,t=0.01 r=10,λ=0.6,A=100,t=0.01

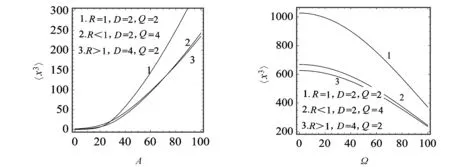
2.4R對三階矩〈x3〉的影響

圖6所示為三階矩〈x3〉作為周期信號振幅A的函數隨R變化曲線圖。從圖6可以看出，〈x3〉是A的單調增函數。當A小于20時，隨著A的增加，三階矩〈x3〉增加趨勢較緩；但是當A大于20時，三階矩〈x3〉則隨著A的增加而迅速增加，而且當R=1時〈x3〉隨著A的增加而增加的趨勢要比R>1和R<1時要快。圖7所示為三階矩〈x3〉作為輸入周期信號頻率Ω的函數隨R變化曲線圖。從圖7可以看出，三階矩〈x3〉是Ω的單調減函數，且當Ω的取值小于20時，〈x3〉隨Ω的增加而緩慢減小；當Ω的取值大于20時， 〈x3〉隨Ω的增加而迅速減小；而且當R=1時，其〈x3〉曲線整體位于R>1和R<1時〈x3〉曲線的上方。

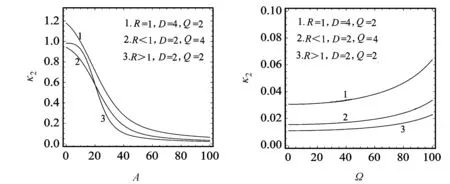
2.5R對態(tài)變量的標準化方差κ2的影響

以輸入周期信號振幅A和頻率Ω為變量，態(tài)變量x的標準化方差κ2在R=1、R>1和R<1時的變化曲線圖如圖8和圖9所示。從圖8可以看出，在R>1和R<1時，隨著輸入周期信號振幅A增加，κ2迅速減小至趨于0附近；但是當R=1時，隨著A增加，κ2先緩慢減小，然后迅速減小，最后緩慢減小至趨于0。從圖9可以看出，κ2隨著周期信號頻率Ω增加在R=1、R>1和R<1時的變化趨勢基本一致：當Ω較小時，隨著Ω增加，κ2基本無變化；當Ω的取值大于60時，κ2則隨著Ω的增加而變大。另外，當R>1時，κ2曲線整體高于R<1和R=1時的κ2曲線。

3 結 語

通過理論計算，得到了關聯噪聲和周期信號驅動下非對稱雙穩(wěn)系統的近似福克-普朗克方程，并在定態(tài)條件下推導了相應的穩(wěn)態(tài)概率分布函數和各階矩的表達式。在定義乘性噪聲強度和加性噪聲強度比率 的情況下，對計算結果進行了數值分析，討論了 對系統的統計性質的影響,對繼續(xù)研究系統的平均首次通過時間、信噪比等具有一定理論指導意義。

[1]Jia Y, Li J R. Stochastic system with colored correlation between white noise and colored noise[J].Physica A,1998,252:417-427.

[2] 寧麗娟，徐偉，楊曉麗.色關聯噪聲驅動的非對稱雙穩(wěn)系統中平均首次穿越時間的研究[J].物理學報, 2007, 56 (1)：25-29.

[3] 周丙常，徐偉.關聯噪聲驅動的非對稱雙穩(wěn)系統的隨機共振[J].物理學報, 2008, 57 (4)：2035-2040.

[4] Wang C J, Dai Z C, Mei D C. Asymmetric effects on escape rates of bistable system [J].Commun Theor Phys,2011,56(6):1041-1044.

[5] 靳艷飛，徐偉，李偉，等. 色關聯的色噪聲驅動的雙穩(wěn)杜芬模型的穩(wěn)態(tài)分析[J].動力學與控制學報，2005,3(2):60-65.

[6] 王兵，吳秀清，邵繼紅.雙色噪聲驅動非對稱雙穩(wěn)系統平均第一穿越時間研究[J].物理學報，2009, 58(3):1391-1395.

[7] 張靜靜，靳艷飛. 非高斯噪聲驅動下非對稱雙穩(wěn)系統的平均首次穿越時間與隨機共振研究[J].物理學報, 2011, 60 (12): 120501-5.

[8] 周丙常，徐偉，張曉燕. 2種不同類型噪聲驅動下的非對稱雙穩(wěn)系統的隨機共振[J].應用力學學報, 2009, 26(1):27-30.

[9] 胡崗. 隨機力與非線性系統[M].上海：上海科技教育出版社，1994.

[10] Liang G Y, Cao L, Wu D J. Approximate Fokker-Planck equation of system driven by multiplicative colored noises with colored cross-correlation[J].Physica A,2004,335:371-384.

[11] Jia Y, Zheng X P, Hu X M, et al. Effects of colored noise on stochastic resonance in a bistable system subject to multiplicative and additive noise[J]. Physical Review E, 2001, 63: 031107.

[12] Luo X Q, Wu D, Zhu S Q. Stochastic resonance in a time-delayed bistable system with colored coupling between noise terms[J].International Journal of Modern Physics B, 2012，26(30):1250149.

O431.2

A

1673-1409(2013)28-0018-04

[編輯] 李啟棟