基于激勵解耦法的汽車動力總成懸置系統優化設計

張興川

Zhang Xingchuan（安徽省汽車產品質量監督站，安徽 合肥 230051）

0 引 言

隨著道路條件的改善和汽車設計的輕量化，發動機成為汽車中的最大振源，動力總成懸置系統作為發動機和車身之間的隔振系統，其性能設計優劣直接影響整車的NVH性能[1]。以往對動力總成懸置系統進行研究時，大多是假設動力總成直接連接到地面上，只考慮動力總成 6自由度模型，未考慮整車其他部分，如副車架、車身、懸架以及車輪等其他彈性基礎對其性能的影響[2-3]。實際上，動力總成懸置系統處于整車復雜的多自由度系統中，與其他子系統存在著耦合作用[4-5]。

文中在對動力總成懸置系統進行優化設計時考慮了底盤系統的影響，根據解耦應該與某一特定的激勵有關的理論，以某國產轎車為例，運用改進的遺傳算法，通過使能量解耦度在轉矩軸方向和垂直方向最大化來尋找懸置系統的最優參數。

1 動力總成與底盤系統耦合模型

懸置系統的研究并不是一個獨立過程，需要考慮到與其他系統的耦合。文中考慮到動力總成和底盤之間的相互作用，建立動力總成和底盤系統的耦合振動模型，如圖1所示。

將動力總成和底盤分別看作6自由度的剛體，位移分別為沿x、y、z軸的平動和繞x、y、z軸的轉動；每個車輪只考慮1個垂直方向的自由度（za1，za2，za3，za4），因此整個耦合系統共有 16個自由度。根據兩系統的耦合作用，不考慮施加到底盤上的激勵，可建立動力總成和底盤系統的耦合運動方程

其中，M為質量矩陣；C為阻尼矩陣；K為剛度矩陣（下標1代表動力總成，2代表底盤）；F1為作用在發動機上的激勵；K12，K21分別為動力總成和底盤系統間相互耦合作用的剛度矩陣；C12，C21分別為動力總成和底盤系統間相互耦合作用的阻尼矩陣。

2 動力總成懸置系統參數優化設計

2.1 目標函數的建立

解耦應該與某一特定的激勵有關，一方面，發動機燃燒的爆發力會引起曲軸扭振，尤其在發動機怠速時，扭振激勵的頻率與懸置的頻率接近，因此這種模態下的解耦是必要的；另一方面，氣缸方向上的內部力以及相關運動也是發動機的主要激勵之一，因此對其垂直方向的解耦性也有較高要求，其他振型的固有頻率控制在一定范圍內即可。因此，建立目標函數如下：

其中，Tθy，Tz分別為系統在轉矩軸和垂直方向上的能量解耦度[5]。

2.2 設計變量

懸置的位置、各向剛度和安裝角度等的改變均會引起目標函數值的變化。由于所設計懸置的安裝方式為平置式，故取懸置位置和各向剛度為設計變量。

2.3 約束條件

1）動力總成各階固有頻率通常可確定在 6～17 Hz之間，以避開其他總成的固有頻率。

2）動力總成繞曲軸方向轉動的固有頻率應小于發動機怠速時激勵頻率的1/2。

3）對于普通橡膠懸置，因為材料與工藝原因，壓剪剛度比值（壓剪比）L應在3～8之間。

4）為了增加支承的使用壽命，需要保證動力總成的最大位移量不得超過10 mm，懸置側向變形不得超過2 mm。

綜上所述，得到動力總成懸置優化設計的數學模型

2.4 優化方法

在算法上選擇表現優異的非支配排序的遺傳算法[6]（NSGA-II），并對其進行進一步的改進，采用改進后的算法求得懸置參數組合的最優解。改進后的算法流程，如圖2所示。運行時的參數為：最大代數為100，種群規模為100，采用十進制編碼，雜交概率為0.8，變異概率為0.07。

3 計算實例

3.1 優化前后解耦效果的比較

以某4缸發動機三點橡膠懸置系統（后懸置為上下體）為研究對象。其怠速轉速為750 r/min，動力總成質量m=214.77 kg，轉動慣量{Ix Iy Iz Ixy Iyz Izx} = {14.326.612.76 -1.42-0.081.65}（kgm2），各懸置點的坐標和剛度如表1所示。

分別計算優化前后的動力總成懸置系統的固有頻率和能量解耦度，如表2和表3所示。可知，相比原系統，優化后系統的各方向解耦度有了很大提高，解耦度均達到 90%以上，其中垂直方向和繞轉矩軸方向分別達到94.0%和96.8%。并且各方向的頻率分布合理，垂直方向頻率為9.74 Hz，避開了前橋與車身的垂直固有頻率。繞曲軸方向頻率為 11.5 Hz，小于發動機怠速時激勵頻率的，可以達到很好的隔振效果。

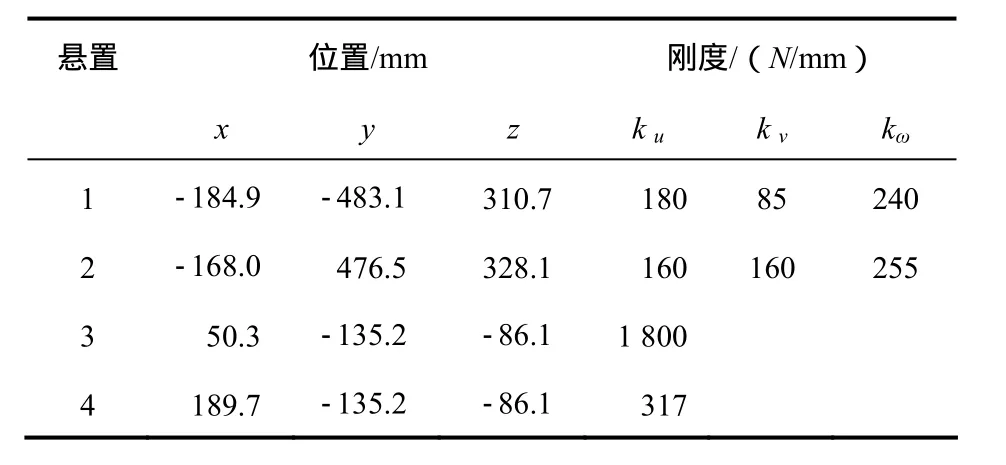
表1 動力總成各懸置參數

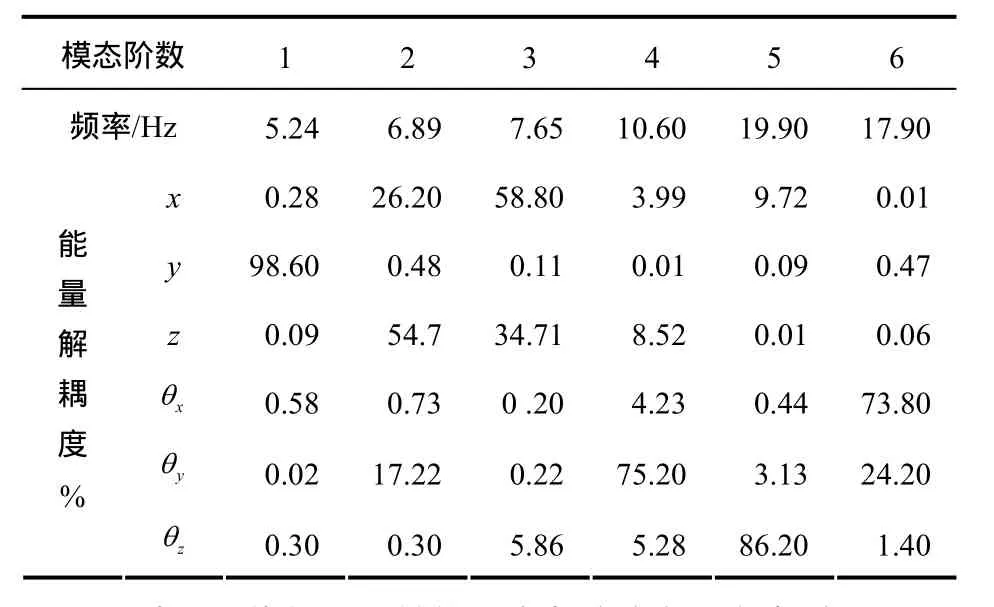
表2 優化前系統的固有頻率和能量解耦度

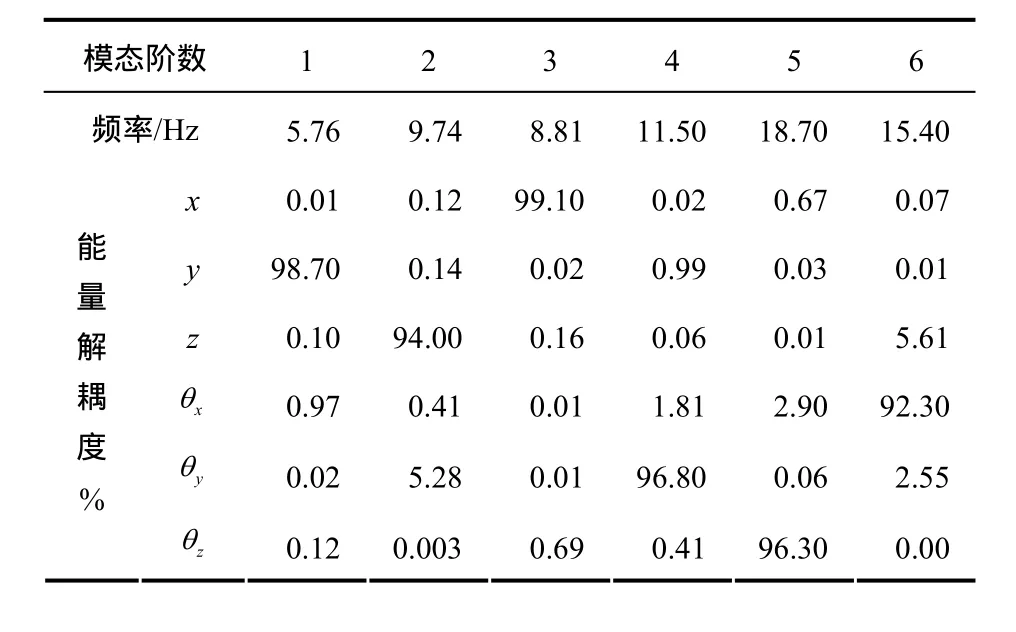
表3 優化后系統的固有頻率和能量解耦度

3.2 整車仿真驗證

懸置系統優化的最終目標是減小車身上關鍵點的振動，考察優化后的懸置系統在整車背景下的隔振效果才最有意義。采用有限元法和多體動力學方法建立整車剛柔耦合模型，并利用輪胎路面工具箱建立輪胎和路面模型，如圖 3所示。通過計算各工況發動機激勵作用下優化前后整車上關鍵點的振動響應，以此預測優化后懸置系統在整車上的隔振效果。

在整車上，取駕駛員座椅下地板A點、副駕駛座椅下地板B點、左側B柱座椅下地板C點、方向盤上的D點等作為振動關鍵點。由于篇幅限制，僅以不同工況時，轉向盤的振動情況為例進行懸置系統優化效果的評價。行駛工況為B級路面，分別計算Ⅲ擋工況下以 80 km/h的車速行駛時，和Ⅴ擋工況下以60 km/h的車速行駛時，懸置優化前后轉向盤中心的垂向振動情況，優化前后的振動加速度曲線分別如圖4和圖5所示。可知，優化后的系統中，轉向盤垂向的振動加速度比優化前有了明顯降低。由此可以看出，采取的優化方案是可行的。

4 結束語

針對懸置系統與其他系統存在耦合作用的問題，建立了動力總成懸置系統與底盤系統的耦合模型。并根據解耦應該與某一特定的激勵有關的理論，結合發動機的主要激勵，以在轉矩軸方向和垂直方向的能量解耦度最大為目標，應用改進的非支配排序遺傳算法對各懸置的位置和剛度進行優化，并將優化前后系統的固有頻率和能量解耦度進行了對比。建立了整車模型，分析了整車中懸置優化前后轉向盤中心的振動情況，結果表明優化后的懸置系統降低了整車的振動，提高了隔振性能，為動力總成懸置系統在整車中的設計提供了參考。

[1]Yu Y.H，Nagi G Naganathan，Rao V. Dukkipati. A literature review of automotive vehicle engine mounting systems [J]. Mechanism and Machine Theory，2001，36（1）：123-142.

[2]Jeong T，Singh R. Analytical Methods of Decoupling the Automotive Torque Roll Axis. Journal of Sound and Vibration，2000，234（1）：85-114.

[3]閻紅玉，徐石安. 發動機—懸置系統的能量法解耦及優化設計[J]. 汽車工程，1993（6）：321-328.

[4]胡金芳，陳無畏.基于彈性支撐的汽車動力總成懸置系統解耦研究[J]. 中國機械工程，2012，23（23）：2879-2885.

[5]Courteille E，Léotoing L，Mortier F，et al. New analytical method to evaluate the powerplant and chassis coupling in the improvement vehicle NVH [J]. European Journal of Mechanics A/Solids，2005，24（6）：929-943.

[6]高媛. 非支配排序遺傳算法（NSGA）的研究與應用[D]. 浙江大學，2006.