基于物理光學假設的導體表面電流密度誤差分析

姬金祖 馬云鵬 黃沛霖 張中建

(北京航空航天大學 航空科學與工程學院，北京100191)

隨著科學技術的發展，隱身技術越來越成為現代戰爭中的一項重要軍事技術［1-3］.在隱身作戰平臺方案論證、概念設計階段，往往通過數值計算得到目標的雷達散射截面(RCS，Radar Cross Section)，以便能夠把握武器平臺整體隱身性能［4-6］，因此快速預估大型目標 RCS非常重要.物理光學法(PO，Physical Optics)是一種重要的RCS快速預估方法［7-9］，其中關鍵的步驟就是通過PO假設得到金屬散射體的表面電流密度.PO法計算表面電流密度基于無限大切平面假設，而且表面電流只存在照明面，陰影面的表面電流為0.根據物理光學假設，僅由入射方向、極化和表面法向就可以計算金屬表面電流密度［10］.

本文對二維情形下基于PO假設的表面電流密度與精確解或矩量法(MoM，Method of Moments)的結果進行對比，研究不同散射體構型、入射波頻率、極化的PO表面電流密度的誤差.極化方面，考慮橫磁波(TM，Transverse Magnetic)和橫電波(TE，Transverse Electric)兩種極化.TM波沿縱向只有電場分量，故電流沿著柱體母線，而TE波沿縱向只有磁場分量，故電流垂直于柱體母線.由PO表面電流計算公式，TM波表面電流隨入射角發生變化，入射角越小，表面電流越大，垂直入射時表面電流最大.而由于TE波磁場強度H總沿著圓柱軸線方向，與表面法向垂直，故照明面表面電流幅度總為磁場強度的2倍［11］.此外，物理光學的表面電流與頻率無關，而實際情況中表面電流的分布與頻率有一定關系［12］.

本文采用導體圓柱、方柱和三角柱這3種構型研究PO法的表面電流密度誤差.這3種構型分別代表了光滑外形、帶有直角棱邊的外形以及帶有銳角棱邊的外形.導體圓柱用精確解作為對比，導體方柱和三角柱沒有精確解，用二維MoM計算結果進行對比.

1 導體圓柱表面電流

導體圓柱邊界面與柱坐標系重合，可由分離變量法結合齊次邊界條件計算得到金屬圓柱表面電流密度分布的精確結果［10］.設圓柱半徑為a，入射電磁波波數為k，電磁波從x軸正向入射，如圖1所示.

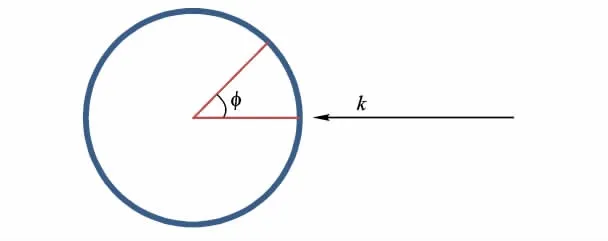
圖1 金屬圓柱電磁波入射方向示意圖

根據分離變量法和TM波、TE波滿足的第一類及第二類齊次邊界條件，可計算得到表面電流沿圓柱分布情況.為分析方便，假設入射平面電磁波H的幅度為1 A/m，計算得TM波和TE波表面電流密度［13］分別為

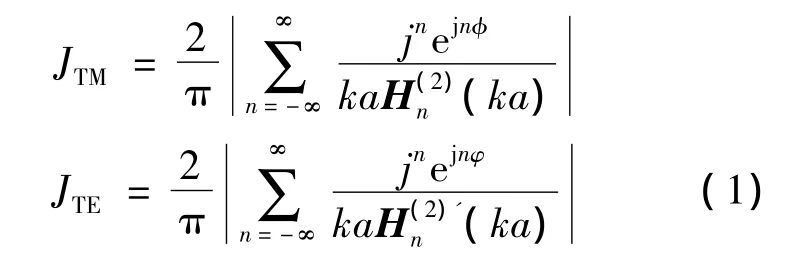
照明面PO表面電流密度計算公式［14］如下:

式中，Js表示表面電流密度;n表示表面法向;Hi表示入射磁場，PO表面電流密度不隨ka變化.計算ka分別為10π，20π和40π時表面電流密度的精確解，并與PO表面電流進行對比.沿金屬圓柱表面均勻選取360個采樣點，用方位角φ表示，單位為(°).TM和TE表面電流密度計算結果對比如圖2、圖3所示.

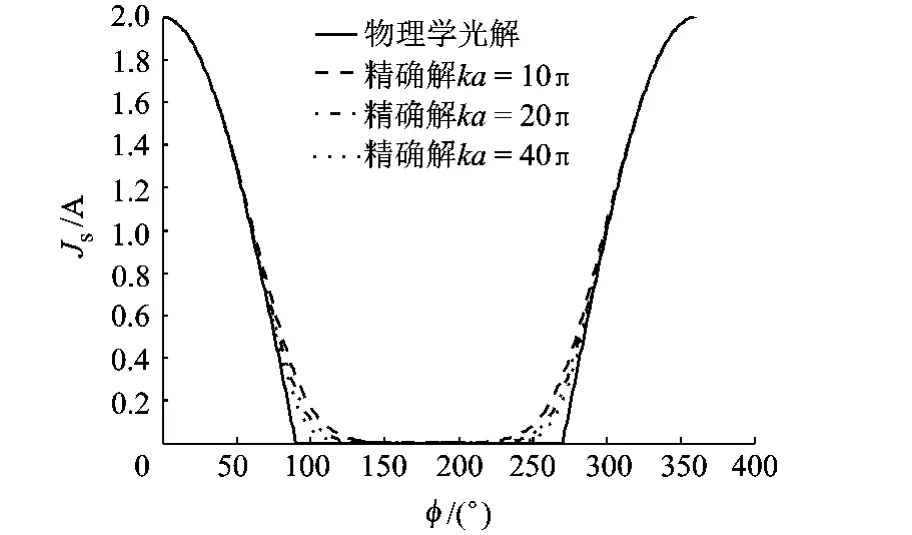
圖2 TM波圓柱表面電流密度

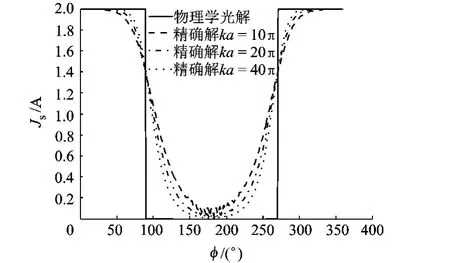
圖3 TE波圓柱表面電流密度

由圖2、圖3可見，TM情形PO表面電流密度與精確解比較一致，而TE情形PO表面電流的誤差較大.兩種極化下，ka越大，PO表面電流與精確解越接近，說明頻率越高，物理光學近似越精確.

用360個采樣點上PO表面電流與精確解之差的均方根來衡量誤差大小，得到均方根誤差隨ka變化的曲線，如圖4所示.

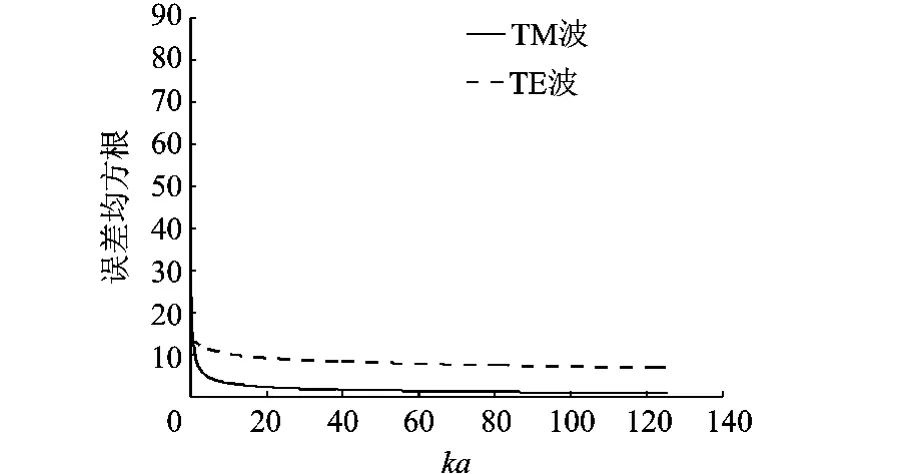
圖4 PO法誤差均方根隨ka的變化

由圖4可見，ka較小時，PO法表面電流誤差很大.隨著ka的增加，PO法表面電流計算結果誤差逐漸減小.但是當ka較大時，誤差隨ka增大而減小的速度變得極其緩慢.比較極化的影響，TM波均方根誤差比TE波小約一個數量級，可見PO表面電流密度在TM極化下精度更高.

2 金屬方柱表面電流

2.1 正入射情形

金屬方柱沒有精確解，本文將PO法表面電流密度與MoM法計算結果進行對比.金屬方柱邊長為2 m，電磁波入射示意圖如圖5所示.

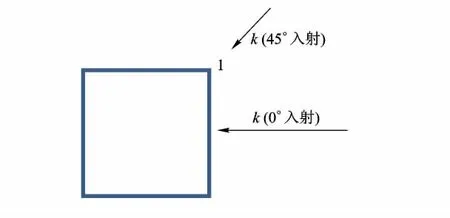
圖5 金屬方柱電磁波入射示意圖

計算入射波長分別為0.5 m和0.2 m時的表面電流密度.MoM法計算中，線元長度設定為波長的1/10，則兩種波長下未知元長度分別為0.05 m和0.02 m，將正方形的邊分別劃分成了160個和400個線元.右上角未知元的編號為1，編號沿逆時針方向增加.MoM法計算表面電流所用基函數為脈沖函數，采用點配法檢驗.

正入射情形，電磁波垂直照射到照明面，在照明面PO法表面電流密度為2 A/m，側面和陰影面都為0.TM和TE情形下電流密度及與MoM法計算結果對比如圖6所示，圖中N表示表面電流元的編號.

由圖6a可見，編號120～160的未知元是電磁波直接照射到的邊，表面電流較大.TM波情形下，PO法表面電流密度較MoM略大，誤差約為0.2 A/m.在電磁波直射的兩個頂點，MoM表面電流密度出現突變，產生峰值，但PO法無法體現這種突變，這是由于TM情形表面電流沿著金屬柱的縱向，故在棱邊能夠產生較強的電流.

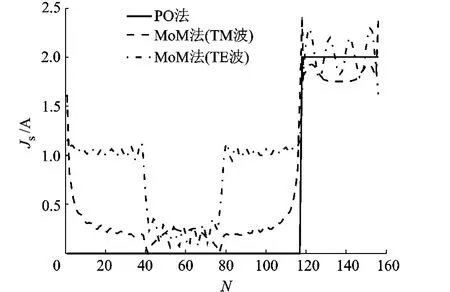
a 波長0.5 m

圖6 0°入射方柱表面電流密度對比

TE情形下，MoM表面電流呈現諧振特性，諧振周期與頻率有關.由于電流沿金屬柱周向，故電流在棱邊傳播受阻，不會產生像TM波一樣的尖峰.金屬方柱邊長為4個波長，而照明面的諧振峰也恰好是4個.TE情形下的諧振峰在PO法假設中無法體現，這也形成了PO的誤差來源.

在電磁波掠入射的邊上(未知元編號1～40和80～120)，PO表面電流為0，但MoM表面電流非零，而且TM和TE還有較大的差別，TM波表面電流密度較小，約為0.2 A/m，而TE波表面電流密度則在1 A/m左右小幅振蕩.比較而言，PO法計算TM波掠入射時的電流較準確，而計算TE波誤差較大.在陰影面(未知元編號40～80)誤差較小，PO法表面電流密度為0，MoM表面電流密度在兩個極化下都與此接近，約為0.2 A/m.

比較圖6a和圖6b兩種入射波長下表面電流的分布，基本特征相似，但有如下細微區別:①波長0.2 m較0.5 m的表面電流密度沿邊長振蕩較快，振蕩幅度較低;②TM情形下，入射波長0.2 m的照明面和陰影面PO誤差較入射波0.5m要大.

2.2 斜入射情形

下面研究入射電磁波沿45°方位角入射到金屬方柱的情形，電磁波照射示意圖如圖5所示.

由于電磁波斜入射到兩條邊上，故TM和TE情形下的PO表面電流密度不同.入射波長0.5 m和0.2 m的表面電流密度分布如圖7所示.

由圖7a可見，編號1～40和120～160的未知元為照明面，其余的未知元為陰影面.TM情形的PO和MoM表面電流密度相差較小，表明TM極化下PO估算的表面電流密度誤差較小.TE情形照明面MoM表面電流密度有較強振蕩，但PO表面電流密度恒為2 A/m.陰影面TE極化MoM表面電流密度為0.5 A/m左右，但PO表面電流密度恒為0，這種情形下，TM極化PO表面電流密度較準確.

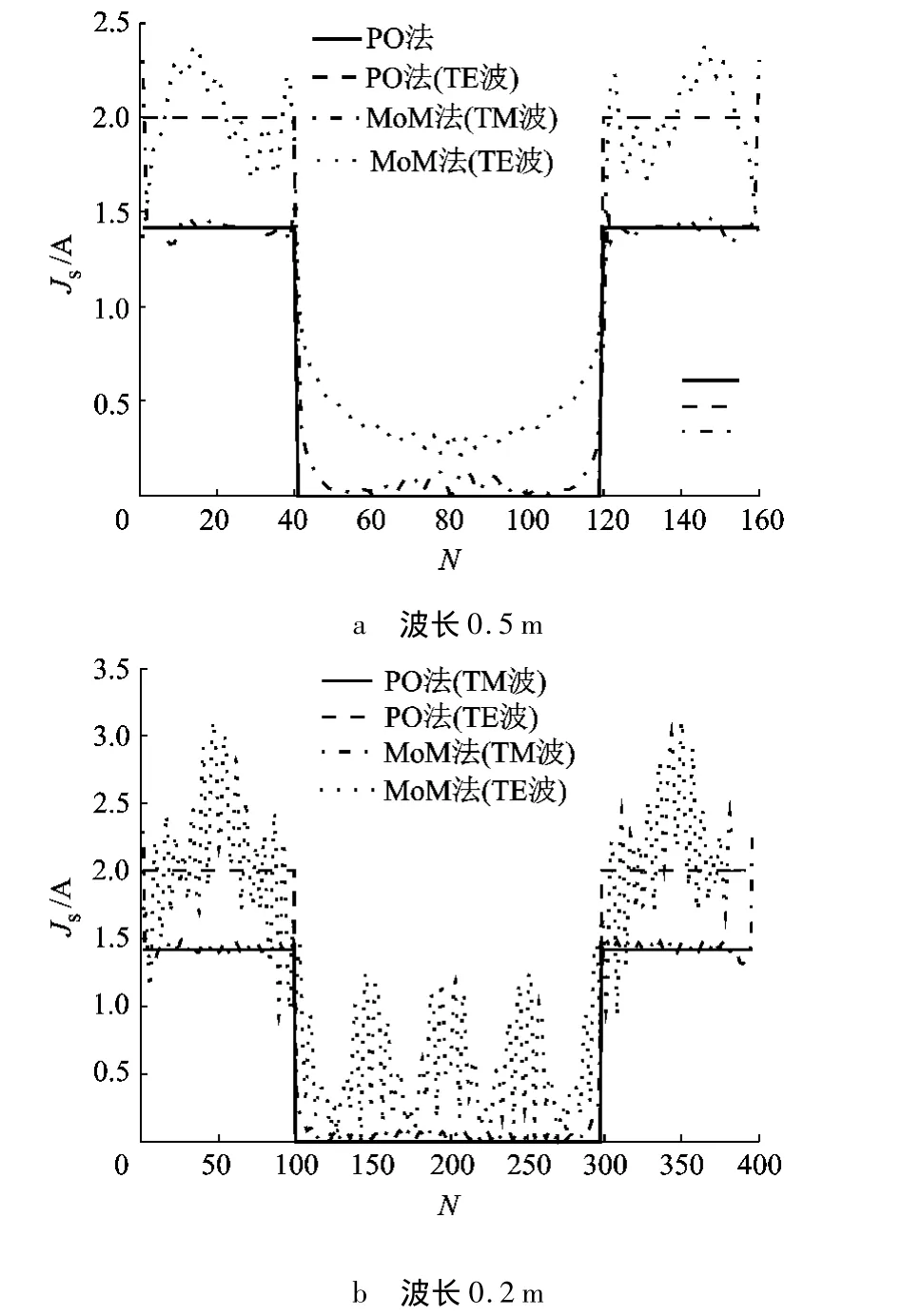
圖7 45°入射方柱表面電流密度對比

由圖7b可見，TM情形PO和MoM計算所得的表面電流密度基本一致.TE情形照明面MoM表面電流密度較入射波長0.5 m振蕩更加劇烈，在陰影面產生了較大振蕩，使PO表面電流密度估算誤差更大.

綜上所述，對金屬方柱，TM波情形PO表面電流估算較為準確，而TE波情形PO表面電流估算誤差較大.隨入射波長見小，誤差加大.

3 金屬三角柱的表面電流

金屬三角柱截面為等腰三角形，高為1 m，底邊長為4 m.設入射波從右側照射到左側，如圖8所示.

圖8 金屬三角柱電磁波入射方位示意圖

設入射波長為0.5 m，將各邊按波長的1/10劃分為線元，共剖分成了167個未知量.用MoM法計算表面電流密度并與PO法結果進行對比.線元編號從左下角頂點開始，逆時針方向增加，如圖8所示.PO和MoM表面電流密度對比如圖9所示.

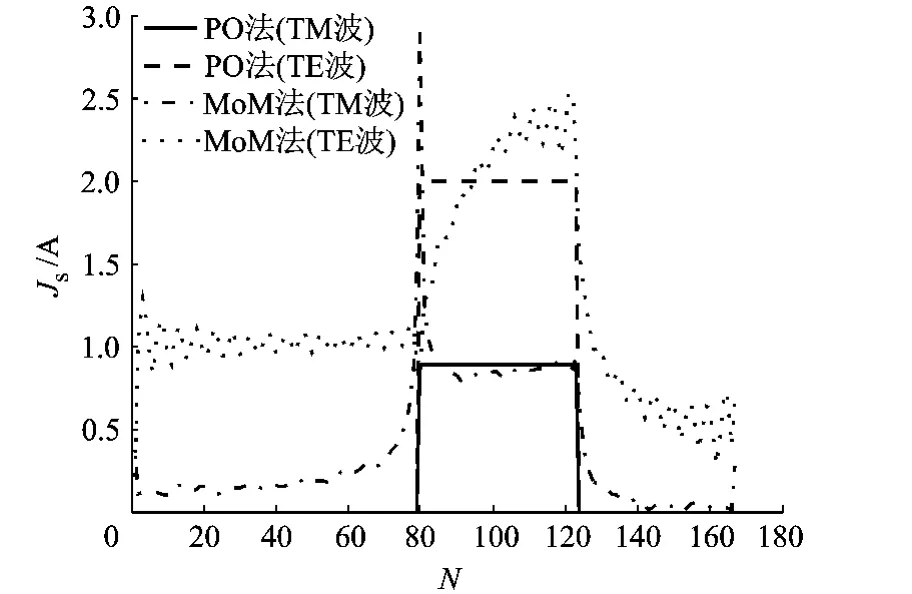
圖9 0°入射三角柱表面電流密度對比

由圖9可見，電磁波0°入射時，只有右側一個面為照明面，對應線元編號為80～123.對TM波，PO和MoM表面電流密度基本一致，誤差主要體現在底邊以及頂點(未知元編號80).MoM法計算得到該頂點電流密度接近3 A/m，但PO法結果還不到1 A/m.在底邊，電磁波呈掠入射狀態，PO表面電流為0，MoM法表面電流密度約為0.25 A/m.

TE波PO表面電流密度為2 A/m，其余面為0.MoM計算結果說明照明面電流密度分布不均勻，基本變化趨勢是從底邊頂點到上邊頂點電流密度逐漸變大，各頂點處也沒有奇異性.在三角形底邊(未知元編號1～80)，MoM表面電流密度在1 A/m上下諧振，這與電磁波掠入射到金屬方柱側面非常類似.左側邊上(未知元編號124～167)MoM表面電流密度約在0.5～1.0 A/m之間.

電磁波從30°方位角入射示意圖如圖8所示.表面電流計算結果對比如圖10所示.

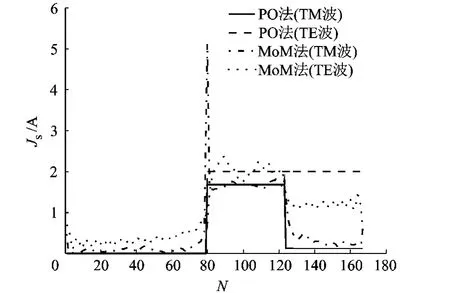
圖10 30°入射三角柱表面電流密度對比

由圖10可見，入射角30°時，三角形的兩個腰都被照射到.TM波情形下，PO和MoM表面電流密度基本比較吻合，但在編號80的未知元處MoM表面電流產生一個尖峰，高達5A/m，這個尖峰在PO表面電流曲線中無法體現.TE情形，在右側邊上(未知元編號80～123)PO和MoM表面電流密度比較吻合，但在左側邊上，電磁波接近掠入射，PO表面電流為2 A/m，而MoM表面電流接近在1 A/m上下振蕩.

4 結論

根據以上PO表面電流密度及其與精確解、MoM對比分析和討論，有以下主要結論:

1)對于光滑表面，如金屬圓柱，TM波表面電流計算結果較為準確，但在TE波情形下誤差較大.PO表面電流分布的誤差隨頻率增加而減少，但變化趨勢隨極化而不同，TM波比TE波的均方誤差更大.

2)對于棱邊的表面，如金屬方柱和金屬三角柱，TM波表面電流密度在棱邊處誤差較大，難以反映棱邊的電流尖峰.在其他地方，PO法估算的表面電流密度比較準確.

3)TE波情形，電磁波掠入射時，表面電流密度恰好約等于入射磁場強度，有小幅振蕩，而PO表面電流密度為0，而且也不能反映振蕩特性.

4)總體而言，TE波PO表面電流密度誤差較大，這是因為TE波照射到目標表面可以很容易形成爬行波，在散射體陰影面形成電流，而TM波的難以形成爬行波，陰影面電流較弱.

References)

［1］姬金祖，劉戰合.基于面元分組的電磁遮擋算法及其優化［J］.北京航空航天大學學報，2009，35(4):453-456 Ji Jinzu，Liu Zhanhe.Electromagnetic occultation algorithm based on facets grouping and optimization ［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35(4):453-456(in Chinese)

［2］ Mohajer M，Safavi-Naeini S，Chaudhuri S K.Surface current source reconstruction for given radiated electromagnetic fields［J］.IEEE Transactions on Antennas and Propagation，2010，58(2):432-439

［3］何國瑜，盧才成，洪家才，等.電磁散射的計算和測量［M］.北京:北京航空航天大學出版社，2006:196-204 He Guoyu，Lu Caicheng，Hong Jiacai，et al.Calculation and measurement of electromagnetic scattering［M］.Beijing:Beihang University Press，2006:196-204(in Chinese)

［4］關瑩，龔書喜，徐云學，等.適用于裁剪NURBS曲面RCS預估的改進的物理光學法［J］.西安電子科技大學學報，2010，37(5):893-898 Guan Ying，Gong Shuxi，Xu Yunxue，et al.Improved PO technique for the RCS computation of targets modeled with trimmed NURBS surfaces ［J］.Journal of Xidian University，2010，37(5):893-898(in Chinese)

［5］陳博韜，雷振亞，謝擁軍，等.基于改進物理光學法的電大目標雙站 RCS的預估［J］.電波科學學報，2010，25(5):960-965 Chen Botao，Lei Zhenya，Xie Yongjun，et al.Bistatic RCS prediction with improved PO method for electrically large targets［J］.Chinese Journal of Radio Science，2010，25(5):960-965(in Chinese)

［6］關瑩，龔書喜，張帥，等.時域物理光學法分析均勻介質目標的瞬態散射［J］.電波科學學報，2011，26(3):515-520 Guan Ying，Gong Shuxi，Zhang Shuai，et al.Transient scattering analysis of electrically large homogeneous dielectric targets by using TDPO method ［J］.Chinese Journal of Radio Science，2011，26(3):515-520(in Chinese)

［7］ Li Jianbing，Wang Xuesong，Qu Longhai.Calculation of physical optics integrals over NURBS surface using a delaminating quadrature method［J］.IEEE Transactions on Antennas and Propagation，2012，60(5):2388-2397

［8］ Jackson J A.Analytic physical optics solution for bistatic 3D scattering from a dihedral corner reflector［J］.IEEE Transactions on Antennas and Propagation，2012，60(3):1486-1495

［9］ Letrou C，Boag A.Generalized multilevel physical optics(MLPO)for comprehensive analysis of reflector antennas［J］.IEEE Transactions on Antennas and Propagation，2012，60(2):1182-1186

［10］ Liu Ziliang，Wang Chaofu.Efficient iterative method of moments physical optics hybrid technique for electrically large objects［J］.IEEE Transactions on Antennas and Propagation，2012，60(7):3520-3525

［11］ Zhang Jun，Yu Wenming，Zhou Xiaoyang，et al.Efficient evaluation of the physical optics integrals for conducting surfaces using the uniform stationary phase method［J］.IEEE Transactions on Antennas and Propagation，2012，60(5):2398-2408

［12］ Huang K，He Z L，Zhang H W，et al.Efficient analysis of antenna around electrically large platform with improved non-uniform rational b-spline hybrid method of moments and physical-optics method［J］.IET Microwaves Antennas and Propagation，2011，5(2):136-141

［13］ Tasic M S，Kolundzija B M.Efficient analysis of large scatterers by physical optics driven method of moments［J］.IEEE Transactions on Antennas and Propagation，2011，59(8):2905-2915

［14］ Umul Y Z.Physical optics scattering of waves by a half-plane with different face impedances［J］.IEEE Antennas and Wireless Propagation Letters，2011，10:21-24