基于強度折減有限元法的邊坡穩定性影響因素敏感性研究

史俊濤，孔思麗，任 琪

（貴州大學土木建筑工程學院，貴州 貴陽，550025）

邊坡穩定性分析是巖土工程及基礎工程領域最重要的研究課題之一。對邊坡穩定性的影響主要有地形地貌、巖土體結構特征以及結構面力學指標、地下水、地震、巖土風化和坡頂超載等因素［1］。這些邊坡穩定性因素的影響程度均較為復雜，其中有些因素具有確定性，但大部分因素卻具有隨機性、可變性、模糊性等不確定性的特點。因此，面對眾多不確定因素，在工程勘察設計中應重點關注其影響較為顯著的因素。傳統的單因素敏感度分析法是設定一個標準值，在保持其他因素不變的條件下，改變其中一個因素，利用基準值－因素變化關系曲線來直觀分析各因素的敏感性大小。盡管上述分析方法較直觀清楚地反映各因素的敏感性大小，但在實際工程中往往伴隨著多種因素的共同改變。雖然正交試驗能夠考慮多因素的共同變化，但卻不能定量地展現各影響因素變化與安全系數的關系。為此，本文以土體邊坡穩定性為研究對象，采用強度折減有限元法分別計算不同黏聚力、內摩擦角、土體重度、彈性模量、泊松比以及坡頂超載大小等因素對邊坡穩定性安全系數的影響，并對均質土坡的單因素敏感度和基于正交試驗多因素敏感度進行分析，以期為基礎工程建設合理地選用邊坡支護的設計與防治措施提供一定依據。

1 基本原理

1.1 正交試驗設計

正交試驗是根據因子的分式原理［2］，利用組合理論推導而成的正交表來安排設計多因素試驗，并對其結果進行統計分析的一種方法。根據正交性，從全面試驗中挑選出部分具有“均勻分散，齊整可比”特點的點進行試驗。本研究對多因素正交試驗結果的分析主要采用極差分析和趨勢分析法。

設A，B，…為不同的因素；r為各因素水平數；Ai為因素A 的第i水平（i＝1，2，…，r）；Xij為因素j的第i水平的值（i＝1，2，…，r；j＝A，B，…）。在Xij下進行試驗得到因素j第i水平的試驗結果指標為Yij，Yij服從正態分布的隨機變量［3］。在Xij下進行n次試驗得到n個試驗結果，分別為Yij（k＝1，2，…，n），其計算參數為

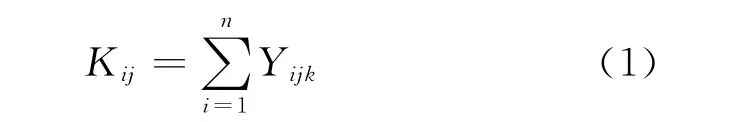
式中：Kij為因素j在i水平下的統計參數；n為因素j在i水平下的試驗次數，Kijk為因素j在i水平下的第k個試驗結果的指標值。

評價因素顯著性的參數為極差Rj，其計算式為［4］

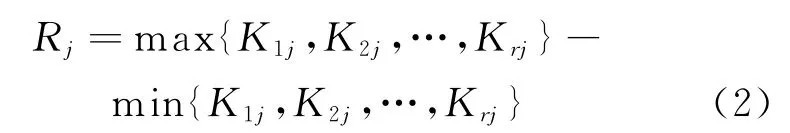
極差的大小代表該因素的水平改變對試驗結果影響的大小，并反映各因素對試驗指標的敏感度大小。

1.2 強度折減有限元法

強度折減有限元法的基本原理［5］是將土體強度參數c、tanφ同時除以一個折減系數F（即采用等比例強度折減的方法），得到新的強度參數c′、tanφ′，然后對邊坡穩定性進行數值分析。通過反復計算達到臨界狀態，直至邊坡發生剪切破壞，此時的折減系數即為安全系數Fs。其分析方程式如下：

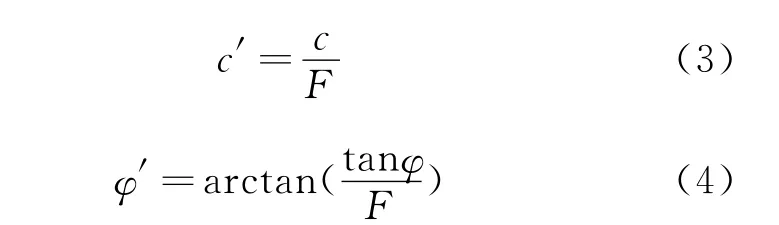
1.3 敏感性分析

邊坡穩定安全系數Fs可視為各個影響因素的函數，即：

敏感性分析［6］是通過邊坡穩定系數的相對變化率與各因素的相對變化率的比值來衡量，即第j個影響因素的敏感度Sj為

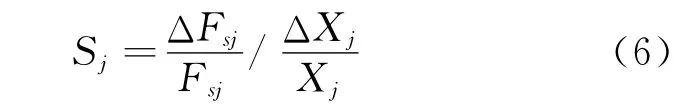
式中：ΔFsj／Fsj為安全系數Fs的相對變化率，ΔXj／Xj為影響因素Xj的相對變化率。

2 邊坡穩定性的計算分析

2.1 工程實例分析

某均質土坡的坡高H 為30m，坡角β為45°，土體重度γ為20kN／m3，黏聚力c為25 kPa，內摩擦角φ為26°，彈性模量E為4000kPa，泊松比μ為0.31，坡頂均布荷載q為100kPa。為了減弱邊界效應的影響，提高其計算精度，按文獻［7］取坡頂到右端邊界的距離為坡高的2.5倍、坡腳到左端邊界的距離為坡高的1.5倍、上下邊界總高為坡高的2倍進行計算。邊坡幾何模型如圖1所示（向右、向上分別為x、y軸正方向）。

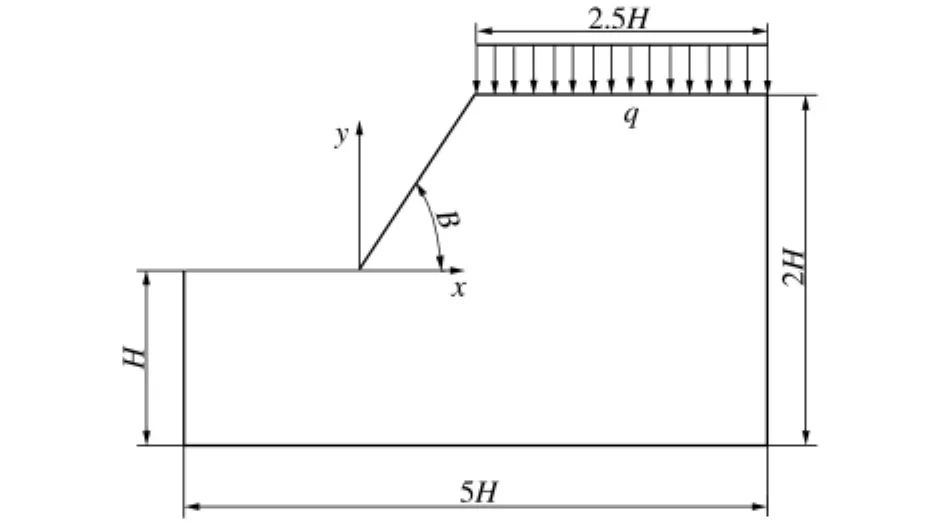
圖1 邊坡幾何模型Fig.1 Geometric model of slope

基于平面應變建立土坡有限元分析模型，土體為服從Mohr－Coulomb屈服準則和非關聯流動法則的理想彈塑性材料，計算步驟采用6節點三角形單元PLANE2進行網格劃分。邊界條件如下：左右兩側為水平位移約束，底部為完全固定約束，上端為自由邊界，局部高應力區域采取細化原則，共分為1139個單元、2370個節點。對于非線性計算采用小變形靜態分析，設置力和位移的收斂標準限值均為0.001，最大的迭代次數為1000次。在進行有限元分析時，采用全牛頓－拉普森迭代法，并采用稀疏矩陣求解器進行求解，以激活自動時間步長，打開自適應下降因子及線性搜索選項。

2.2 正交試驗方案

基于強度折減有限元法對不同黏聚力A、內摩擦角B、容重C、彈性模量D、泊松比E、坡頂均布荷載F等影響因素作用下的邊坡安全系數進行計算，每個因素選擇5個水平對邊坡穩定性進行正交分析。假定各因素之間無交互作用，則對所研究的6種因素選擇正交表L25（56）安排正交試驗。如果全面進行試驗，則需要15625次，但采用正交表L25（56）來安排試驗，試驗次數僅為25次。各因素取值范圍和水平如表1所示。

表1 各個影響因素的取值范圍和水平Table1 Factor value and level

2.3 多因素極差分析

表2為正交試驗方案及計算結果。對各個因素相同水平的試驗結果求平均值，然后用各個水平平均值中的最大值減去最小值求得極差。極差的大小反映了該因素水平的改變對安全系數影響的程度大小，因此通過極差的大小可找出影響試驗結果的主要因素和次要因素。對表2的試驗結果進行極差分析后，其計算結果如表3所示。由表3可看出，6個因素敏感性大小排序依次為：內摩擦角、黏聚力、土體重度、坡頂荷載、彈性模量和泊松比。按照安全系數Fs取得最大值，可以確定最優方案為A2B1C2D3E4F5。

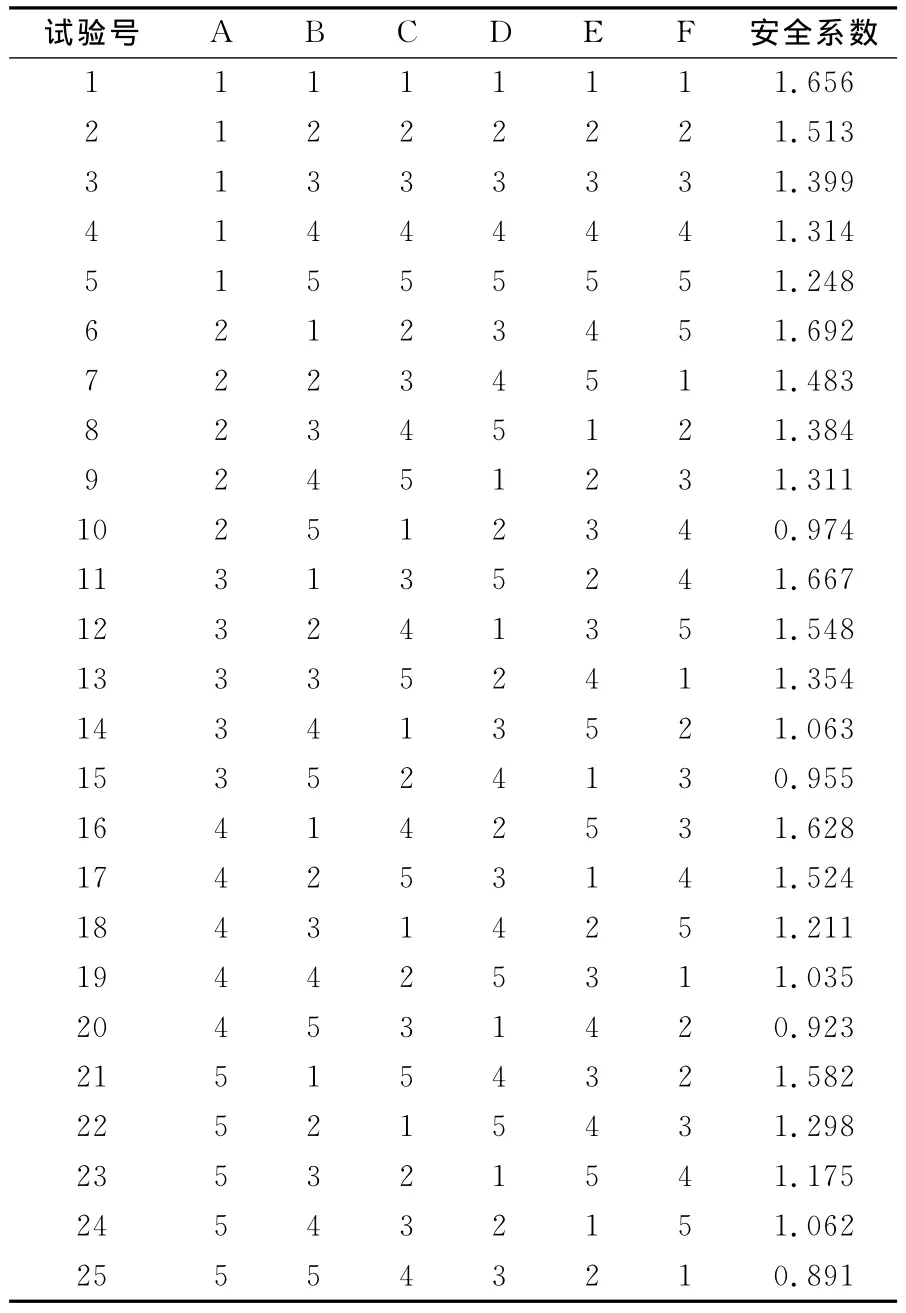
表2 正交試驗方案及計算結果Table2 Test schemes and calculation results of orthogonal design

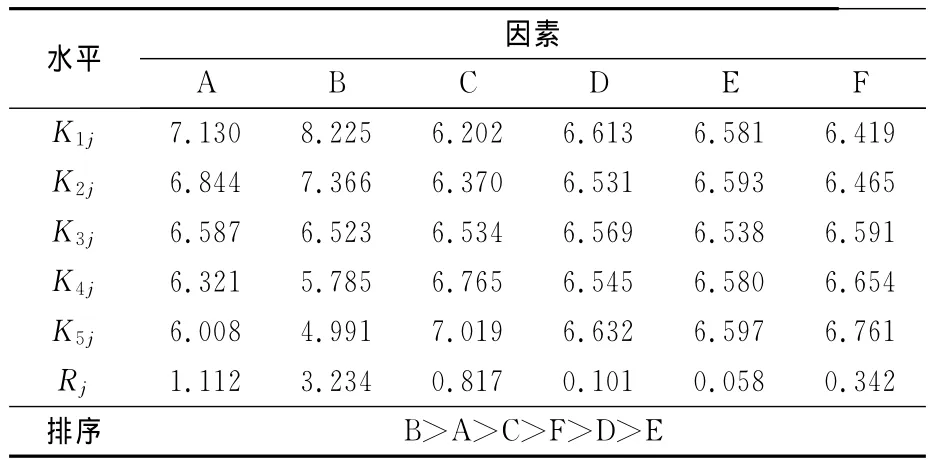
表3 極差分析結果Table3 Range analysis results

圖2為各個因素趨勢的分析結果。由圖2可看出，在坡頂荷載作用下，內摩擦角對邊坡穩定性影響最為顯著，坡頂荷載、彈性模量、泊松比大小的變化對安全系數的影響不大。隨著坡頂荷載的增大，安全系數減小幅度不大，但安全系數隨著內摩擦角、黏聚力的增大而呈明顯增大趨勢，但隨著土體重度的增大而呈明顯減小趨勢。

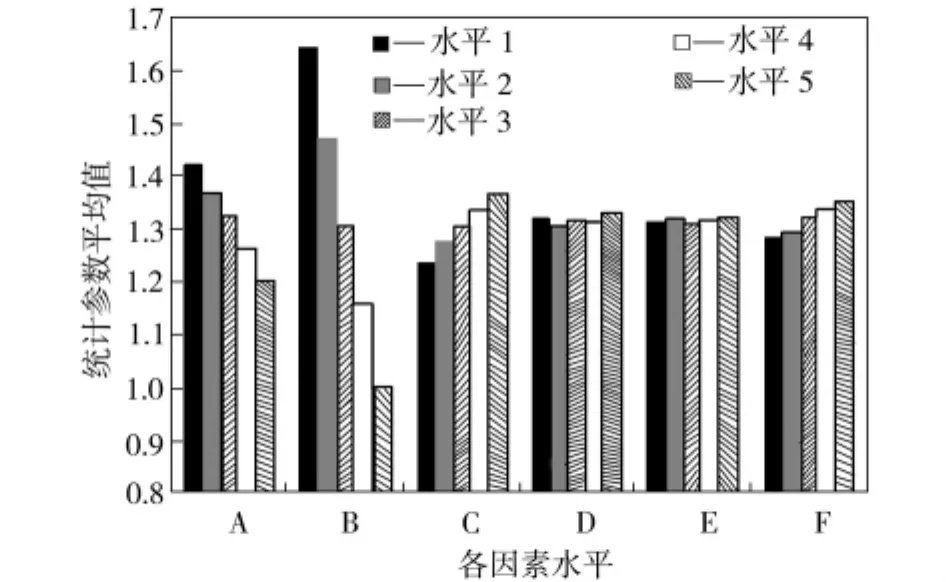
圖2 各個因素趨勢分析結果Fig.2 The trend analysis for every factor

2.4 單因素敏感性分析

由于實際問題中各個因素具有不同的量綱，不便于比較分析，因此，本文采用各個因素的相對變化率與邊坡穩定安全系數間的關系曲線來進行單因素的敏感度分析。圖3為各個影響因素的變化率與邊坡穩定安全系數間的關系曲線。由圖3可看出，在超載作用下，邊坡穩定安全系數隨著內摩擦角、黏聚力的增加近似地呈線性增大，這是由于土體內摩擦角、黏聚力增加后，其抗剪強度增大，抗滑力隨之增加。內摩擦角每增大1°，其相應的安全系數平均增加0.0421；黏聚力每增加1 kPa，其對應的安全系數平均增加0.0142。邊坡穩定性安全系數隨著坡頂超載、土體重度大小的增加而呈線性減小。土體重度每增加1kN／m3，其穩定安全系數平均降低0.0128；坡頂超載每增加1kPa，其對應的安全系數平均降低0.00125。

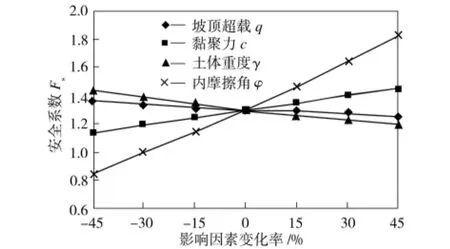
圖3 邊坡穩定安全系數與影響因素的敏感性關系Fig.3 Relation between safety factor and sensitivity of slope

根據單因素敏感分析法，由式（6）計算可得各個影響因素單獨變化時所對應的敏感性系數如表4所示。由表4可看出，在坡頂荷載作用下，內摩擦角的影響最為顯著，坡頂超載影響最小，其敏感性大小依次為內摩擦角、黏聚力、土體重度和超載大小。這表明坡頂超載時，在這4種影響因素中土坡自身的物理力學特性占主導因素，坡頂超載參數的變化為誘導因素。

表4 單因素變化條件下的敏感系數Table4 Sensitivity coefficient under single－factor transformation

通過上述對比分析可知，單因素敏感性分析與多因素正交試驗極差分析在評價各個因素對邊坡穩定性的敏感度大小上可得出一致結論。在判定對邊坡穩定性影響較小因素（如彈性模量、泊松比）敏感度大小的問題上，采用多因素正交試驗極差分析法的計算結果較單因素敏感性分析簡潔直觀，但前者只能定性評價各個因素對邊坡穩定性的影響程度，而后者可得出各個因素參數的改變與邊坡穩定安全系數變化的關系曲線，并能反映其參數的改變對邊坡穩定性的影響規律。

在實際工程中，邊坡土體的強度指標和幾何指標均在一定的范圍內變化，為了增大安全系數而無限制擴大其范圍既不科學也不經濟，因此應當采用合理的措施來改善邊坡的穩定性狀態。在超載作用下，內摩擦角的影響最為顯著，然而對于黃土［8－10］等特殊土質而言，其內摩擦角的變化范圍一般為15°～30°，僅通過增大內摩擦角對提高邊坡整體安全系數貢獻不大。在此種情況下，需采用錨桿支護措施來提高土體的黏聚力，以便進一步提高邊坡整體穩定性的效果。因此，在邊坡防治時，要考慮工程地質環境和邊坡巖土體自身特性，綜合采用多種支護措施進行邊坡的治理，以便更加合理、有效。

3 結論

（1）多因素正交試驗極差分析與單因素敏感性在評價各個因素中對邊坡穩定性的敏感度大小具有一致性。在超載作用下，內摩擦角對邊坡穩定性的影響最為顯著，泊松比對邊坡穩定性的影響最小。在一定的參數變化范圍內，敏感性大小的排序為：內摩擦角、黏聚力、土體重度、超載大小、彈性模量和泊松比。

（2）坡頂荷載作用下，土體的抗剪強度指標和重度是影響邊坡穩定性的主要因素，其參數的變化對邊坡的穩定性有顯著影響。

（3）考慮到坡頂超載作用，隨著超載大小、土體重度的增加，邊坡穩定安全系數大致呈線性減小；隨著其內摩擦角、黏聚力的增加，邊坡穩定安全系數大致呈線性增大。

（4）在判別對邊坡穩定性影響較小因素的敏感度大小問題上，多因素正交試驗極差分析法較單因素敏感性分析簡潔直觀，但極差分析法只能定性分析各個因素對邊坡穩定性的影響程度，而單因素敏感性分析可得出各個因素參數的改變與邊坡安全系數變化的關系曲線，并能反映其參數的改變對邊坡穩定性影響的一般規律。因此在實際工程中，建議二者結合進行綜合判定各個因素對邊坡穩定性的敏感程度，以便得出合理、適用的結論。

［1］張咸恭，王思敬，張倬元，等.中國工程地質學［M］.北京：科學出版社，2000.

［2］孫棟梁，楊春燕，候克鵬.基于正交設計的邊坡穩定性影響因素敏感性分析［J］.昆明冶金高等專科學校學報，2005，21（5）：10－13.

［3］張旭輝，龔曉南.邊坡穩定影響因素敏感性的正交法計算分析［J］.中國公路學報，2003，16（1）：36－39.

［4］陳希孺.數理統計引論［M］.北京：科學出版社，1997.

［5］徐千成，鄭穎人.巖石工程中屈服準則應用的研究［J］.巖土工程學報，1990，12（2）：93－99.

［6］周佳榮，易發成，候莉.多因素作用下邊坡穩定影響因素敏感性分析［J］.西南科技大學學報，2008，23（2）：31－36.

［7］張魯渝，鄭穎人，趙尚毅，等.有限元強度折減系數法計算土坡穩定安全系數的精度研究［J］.水利學報，2003（1）：21－26.

［8］張少宏.黃土邊坡穩定計算中參數的敏感性分析［J］.水利與建筑工程學報，2003，1（3）：41－42.

［9］陳志波，簡文彬.邊坡穩定性影響因素敏感性灰色關聯分析［J］.防災減災工程學報，2006，26（4）：473－475.

［10］王四巍，劉海寧，劉漢東.黃河下游堤防邊坡多因素敏感性分析［J］.人民黃河，2009.31（7）：18－19.