時差定位模型與定位精度分析

楊俊峰

（中北大學 電子測量技術國家重點實驗室，山西 太原 030051）

1 引言

多點無源時差定位技術已在軍事、民用等各個行業中得到廣泛應用，多點定位技術已從基本的三站時差向多站、多站組網技術發展。隨著網絡時代的來臨，軍事應用中的防空網、民用中的無線手機蜂窩定位、民航場面監視／航路監視系統等都面臨著對時差定位技術更深層次的開發和應用。工程應用中，首先面臨的是時差定位體制和技術途徑的選擇。時差定位的單元數量為3個或3個以上的接收站，時差提取可以是各站時間同步和協同轉發同步兩種方式。定位求解過程通常要確定接收主副站，為了簡化定位模型，坐標系原點選在主站上，從而構造一系列副站相對主站的距離差方程，獲得目標求解。

定位誤差是描述定位精度性能的參考指標，本文基于工程中不同定位幾何模型對定位精度的不同程度影響，詳細分析了幾種不同的定位幾何模型在不同區域處的定位誤差分布情況。

2 定位原理

對目標進行定位，實質上是一種無源定位技術，采用多站側向交叉的方法來實現對目標的定位。目標定位系統的每個基站通常由長基線組成，接收基站由4個以上接收傳感器陣元按某種幾何關系進行布陣。由于各傳感器接收信號時無法實現同步，只能利用信號到達N個傳感器之間的時延差，建立雙曲面交匯模型求解目標位置。

建立三維坐標系，xoy面平行于水平面。Oz軸與xoy平面垂直指向上方。設目標位置坐標為（x，y，z），4 個基站的坐標分別為（xi，yi，zi），（i=0，1，2，3）。目標到基站的距離為ri（i=0，1，2，3）。目標到各分站與主站（基站0為主站）的距離差為ri0。目標定位示意圖如圖1所示。根據時差定位原理有如下關系：

其中，ti0表示目標信號到達分站與主站之間的時間差，c為波傳播的速度。

圖1 目標定位示意圖

3 定位精度評價指標

為了評價各種不同布站方案的優劣以及不同定位算法的性能，首先需要明確的是定位精度的評價指標。較為常用的評價定位精度的指標主要有絕對誤差、相對誤差、均方誤差（MSE）、均方根誤差（RMSE）、幾何精度因子（GDOP）等。其中幾何精度因子（GDOP）用來評價基站的布設位置對定位精度的影響。

幾何精度因子GDOP是評價基站幾何位置坐標對定位精度影響的重要指標，其值為定位誤差RMSE與測距誤差RMSE的比率。對于無偏差的估計器，GDOP為

GDOP 主要用來度量幾何位置對定位精度的影響程度，GDOP 值越大，定位精度越低，相反，GDOP 值越小，定位精度越高。因此，可用 GDOP 來描述定位精度。

4 仿真分析

以下仿真都是在基于傳播介質為均一介質，即目標源發出的波在介質中以勻速傳播的假設下進行的。設初至波的在介質中的傳播速度是 400m/s。目標范圍是x方向0～20m，y方向-9m—9 m，z方向-1m。

下面以四傳感器基站為例，在相同的傳感器基站站址測量誤差0.01 m和初至波到時差測量誤差50us的情況下，傳感器基站布設z方向不超過-1m。對不同幾何布設的定位精度進行仿真。傳感器基站布設情況如圖 2所示。

圖2 不同幾何布站在二維平面示意圖

不同幾何布站下的震源定位精度情況如圖3所示。

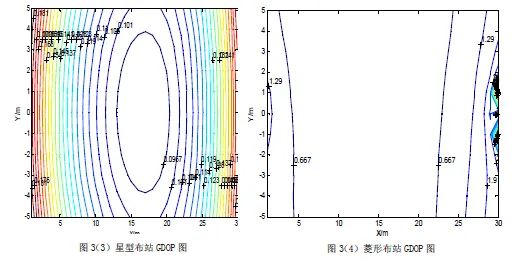
從圖3中四種布站下的GDOP圖中，可知星型布站的定位精度最高；平行四邊形布站的定位次之，其在X軸方向的定位精度要高于Y軸；菱形布站和倒三角布站的定位精度較差。

5 結束語

通過理論推導和誤差仿真實驗結果都可以看出，傳感器基站的幾何布站方式對目標定位精度也有很大的影響，以四基站布設為例，在倒三角布站、平行四邊形布站、星型布站以及菱形布站這四種形式中，星型布站的定位精度最高；平行四邊形布站的定位精度次之，其在 x 軸方向的定位精度要高于 y軸；倒三角布站及菱形布站的 GDOP 分布基本呈紡錘形，定位精度較差。仿真的結果可供工程參考。

[1] 高海艦，李陟.多站組網時差測量定位精度算法研究[J].系統工程與電子技術，2005，27（4）：578-581.

[2] 菌強，吳德偉，毛玉泉.多基站無源定位技術在區域定位網絡中的應用[J].現代雷達，2007，29（8）：12-14.

[3] 孫仲康，周一宇，何黎星.單多基地有源無源定位技術[M].北京：國防工業出版社，1996.

[4] TORRIERI D J.Smfistieal Theory ofPassive Location Sys.terns[J].IEEE Tram Aerosp Electron Syst，1984，20（2）：183-198.

[5] 王瀚，鐘丹星，周一宇.不規則布站時差定位系統定位精度分析[J].現代電子技術，2007（7）：19-21.24.

[6] 楊政.提高時差定位精度的方法[J].電子信息對抗技術，2007，22（4）：9-11，53.

[7] 胡來招.無源定位[M].北京：國防工業出版社，2004.

[8] 呂世超.微地震有效事件識別及震源自動定位方法研究[D].青島：中國石油大學，2011.

[9] 陳玲，李少洪.無源測向測時差定位算法研究[J].電子與信息學報，2003，5.