基于排隊論的西安國際港務區公交優化研究

常 瑤

(陜西鐵路工程職業技術學院，陜西渭南 714000)

1 問題的提出

作為我國西部大開發的重點城市，西安一直是國家著力促進建設的城市之一。憑借其優越的地理位置、便利的交通以及兼容并包的城市發展戰略，西安成為西部重要的經濟中心和交通樞紐，推動著地區經濟的進步和城市發展。通過與上海市合作建設的西安國際港務中心，旨在打造中國第一大無水內陸大港，它的建成必會大大提高地區的經濟實力，有助于實現我國西部內陸地區物流集散，集裝箱貨運等功能。

西安國際港務中心位于西安市灞橋區新筑境內。新筑鎮是一個擁有4萬人口的新型城鎮，國際港務區的建成將會進入大批人流和物流，屆時該地區原著居民的日常出行以及港務區內工作人員的通勤都會對交通產生很大影響。然而該地區的公交現狀則不容樂觀:西安現共有197條公交線路，其中只有10條線路經過灞橋區，僅占公交車總數的5%左右;經過國際港務中心所處新筑鎮的公交更是少之又少，只能坐233路到霧莊下車，然后還要一直向北走幾百米的距離;而233是一個中巴車線路，通常在霧莊站點處人流量很大，車上也比較擁擠。公交車的狀況如不及時得到改善將會大大制約國際港務區的發展。

本文旨在解決以上問題，通過運用排隊理論建立合理化模型探索其對該區域公交的影響，優化公交現狀，方便市民出行和促進周邊經濟發展，解決制約港務區發展的問題，實現其經濟效益和規模效益的最大化。

2 運用排隊論進行公交優化

2．1 客戶到達速率λ的獲取和檢驗

客戶到達情況的了解采用實地觀測法［1］。通過連續一個月的調查發現，該地區人流量在時間上和地域上存在差距，故選取西安國際港務區附近的兩個路口:一個是人流量較多的港務大道東三環附近的路口;另一個是人流量較少的312國道和紡渭路交界的路口。根據實地調查發現，該地區的人流量時間性差異明顯，選取有代表性的兩個時間段:上午10:00～12:00和下午16:00～18:00作為統計數據，每分鐘統計一次，共得到480個數據，將這480組數據整理便得到顧客到達的數目和頻數的關系，見表1。

表1 顧客到達的數目與頻數的關系

對客戶到達的速率λ服從的分布進行檢驗:通常我們采用X2檢驗法［2］來檢驗在時間間隔t內出現的事件流X(t)是否服從泊松分布。通過計算得出輸入數據流的理論頻數npi與實測頻數ni，在某一確定的置信區間內對其進行假設檢驗，如果符合條件則接受該假設，即該樣本服從泊松分布;反之，不服從泊松分布。選取顯著性水平為0．05，根據上述已知的乘客到達數目與頻數的統計數據，運用χ2檢驗法對乘客到達的速率λ進行假設檢驗。

設H0:客戶到達率λ服從泊松分布;H1:客戶到達率λ不服從泊松分布。

在H0為真時，運用公式:

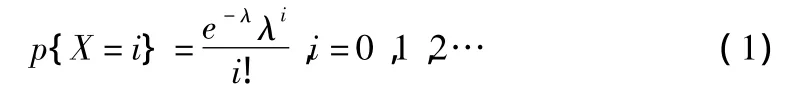
因為在H0中參數λ未具體給出，故需要先估計λ。采用極大似然估計法，根據公式:

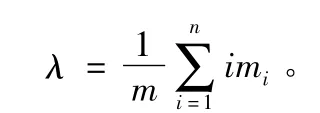
求得:

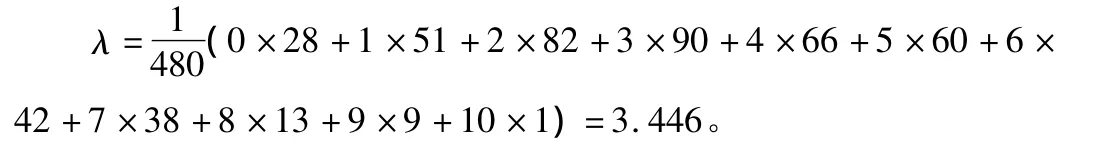
即 H0:X(t)～P(3．446)，本例中只觀測到0，1，2，…，10 共11 個不同的值，這相當于把總體X(t)分成11類，在原假設下，每類出現的概率為:

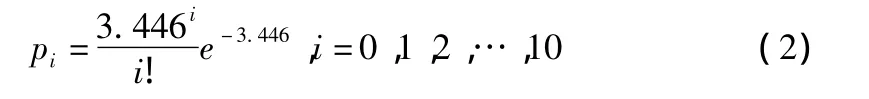
選取統計量:

根據式(2)和式(3)可以檢驗統計量 χ2的值，具體計算過程如表2所示。

表2 統計量的計算結果

2．2 模型優化分析

令N(t)表示在時間(0，t)內到達的乘客數，由于乘客到達服從泊松分布，所以具有該分布的特點［3］。

1)N(0)=0，即在0 s內沒有顧客到達。

2)獨立性，即在時刻0，t1，t2，…，tn到達的顧客相互獨立。

3)在(t，t+Δt)時間內到達的顧客只與時間間隔Δt有關，與起始點無關，即對任意的 t∈［0，T］，有:

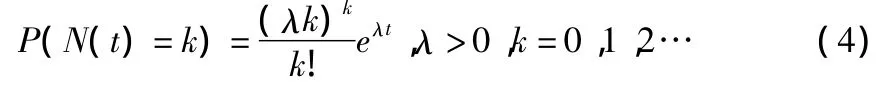
排隊論理論是對一系列隨機過程進行的優化分析，所以在構建模型之前要先分析輸入流和輸出流的隨機性特點，由于本文主要研究的是排隊論在西安國際港務區公交線路優化方面的問題，所以以車站到達的乘客流為輸入流，將公交車視為服務臺。根據調查和比較分析可得服務臺服務時間服從負指數分布，具體檢驗方法與之前所列類似，在此便不再贅述。假設每分鐘經過一趟公交車，每次公交車能承載的人數不同，經過統計測算每一趟車平均裝載6人，根據排隊論的基本理論，可以求出這個排隊模型中需要排隊等待服務的概率、不需等待的概率以及其他數量指標。根據泊松分布的特點，乘客接受服務的時間間隔具有無記憶性，也是相互獨立的，所以服從負指數分布。

由式(4)可知:

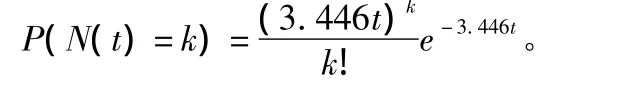
因為每分鐘經過一趟公交車，且每次平均載客6人，則乘客乘坐公交車平均時間為6人/min，即該排隊系統的平均服務率為μ=6，服務臺的服務強度=0．574，則根據公式排隊論相關公式可以求得其他數量指標:

系統中有零位顧客的概率 P0=1-ρ=1-0．574=0．426，即顧客到達后不需要等的概率，而顧客到達后需要排隊等的概率為ρ =0．574。

顧客在系統中平均逗留時間:

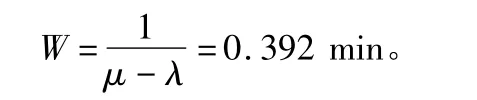
顧客在系統中平均等待時間:

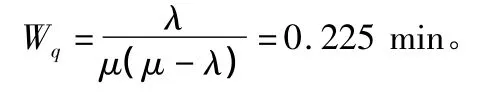
3 結語

在上面這個排隊模型中，公交車的頻率決定了公交公司運營的費用高低，同時也決定了乘客等待時間的長短。頻率過高，費用大幅增加，大大減少了公交公司的效益，不利于公司的發展;頻率過低，導致乘客等待時間過長，不能很好履行公交車方便市民的義務，產生不利的社會影響，最終也會影響到公交車的運營。因此平衡好這二者之間的關系便顯得至關重要。

下面通過計算對上面的例子作進一步分析，根據模型中的公式，可以算出服務臺的增減對等待時間產生的影響，具體數據如表3所示。

表3 服務臺的增減對等待時間的影響

由表3可知，如果將公交車的頻率降低為半分鐘一趟，會大大減少等待時間，但是需要多投入一倍數量的公交車，總成本會大幅提高;若是增加到一分半一趟，公交公司的成本降低了，不過延長了乘客的等待時間，對提高市民生活質量帶來不利影響。所以只有正確處理好二者關系，才能更好發揮公交的優勢，緩解交通壓力，方便市民出行。

［1］楊茂盛．運籌學［M］．西安:陜西科學技術出版社，2006．

［2］劉瑞元，張智霞．二項分布與泊松分布判別的假設檢驗［J］．青海大學學報，2008，26(1):44-47．

［3］王東升，劉玉堂．泊松過程在排隊論中的應用［J］．河南機電高等專科學校學報，2004，15(4):121-125．