遺傳算法在高負載XMPP中的路徑優化應用

陳雙喜 吳湘蓮 蔡向東 黨中華

(嘉興職業技術學院 信息技術分院，浙江 嘉興 314036）

XMPP(Extensible Messaging and Presence Protocol，可擴展消息與存在協議)是目前主流的四種即時消息(IM：Instant Messaging)協議之一。它是一種基于XML的協議，繼承了XML靈活性和擴展性。目前，XMPP采取Pastry算法進行路徑優化[1,2]。物聯網研究領域曾有提議，將XMPP作為物聯網通信標準[3]。但是礙于在高負載條件下 Pastry算法對消息傳輸沒有進行延時控制，可能會導致垃圾信息充斥整個網絡，使得網絡性能下降。因此有必要對XMPP路徑優化問題進行探討。

遺傳算法（Genetic Algorithm）是一類借鑒生物界的進化規律演化而來的隨機化搜索方法。它采用概率化的尋優方法，能自動獲取和優化搜索空間，自適應地調整搜索方向，不需要確定的規則。目前，遺傳算法已被成功應用到規劃、控制、設計等領域用來求解實際問題，并且展現出廣泛的應用前景[4-6]。在XMPP網絡中，路徑選擇具有很強的隨機性和復雜性。高負載條件下，如果網絡能夠自動優化路徑，網絡的工作效率將得到提高。因此本文采用遺傳算法來嘗試解決XMPP在高負載條件下路徑優化問題。

1 高負載路徑優化問題

1.1 問題描述

高負載路徑優化問題描述為：已知數據包在XMPP網絡中的起始節點和目標節點間傳送，求數據包從起始節點到目標節點的最優路徑。其中最優路徑需滿足以下條件：

（1）起始節點和目標節點不屬于同一條線路；

（2）從起始節點到目標節點的路徑必須是連通的；

（3）從起始節點到目標節點的路徑中不允許有回路。

實際應用中的XMPP系統規模比較復雜[7]，我們在求解優化路徑時需先對其進行簡化。

圖1 簡化的XMPP系統結構

在簡化的XMPP系統結構圖中，我們將XMPP網絡上的所有節點分為：服務器節點和終端節點。其定義如下：

定義1：完成XMPP數據轉送、備份、路徑選擇等處理操作的設備的稱為“服務器節點”。如圖1中的XMPP Server節點；

定義2：完成客戶端數據接收、發送、數據協議轉化等操作的節點稱為“終端節點”，如圖1中的End節點。

根據上述定義，路徑可以分為服務器節點到服務器節點、終端節點到服務器節點以及服務器節點到終端節點三類路徑。由于后兩類路徑不需要其它服務器節點進行傳遞，其路徑的求解可以轉化為對第一類路徑的求解，因此在建立XMPP網絡路徑模型時只需考慮服務器節點與服務器節點間的最優路徑。

1.2 簡化的XMPP網絡模型

簡化后的XMPP網絡模型用有權無向圖G=（V，E，C）來描述，其中：

（1）V是XMPP網絡中終端節點和服務器節點的集合。用一組從1開始的連續自然數逐條對XMPP網絡中的不同節點進行編號，每個節點擁有唯一的編號。因此，V是由一組連續的自然數組成的集合；

（2）E 是圖中邊的集合，邊（i，j）表示節點 i和 j之間存在線路；

（3）C=[Cij]是權值矩陣。 Cij表示邊（i，j）上的權值，即從節點 i到節點j之間執行效率。取值范圍為大于等于零。在實際的XMPP網絡模型中，邊上的權值取決于所有相鄰兩服務器節點的執行效率。為零時表示斷路，權值越大，執行效率越高；

（4）高效路徑的選擇依據C和E的值進行判斷，權值越大，邊數越少，優先選擇。

圖2是簡化后的XMPP網絡模型圖：

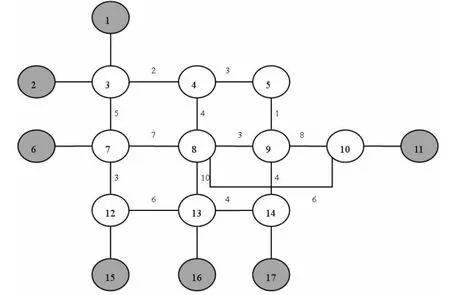
圖2 簡化XMPP網絡模型無向圖G

如上圖所示，從終端節點1到終端節點16，存在多條可選路徑。例如包括：（3，7，12，13）、（3，4，8，13）、（3，7，8，13）和（3，4，5，9，14，13）四條路徑，這四條路徑的權值和分別為：14(5+3+6)，16(2+4+10)，22(5+7+10)和 14(2+3+1+4+4)。 節點的個數分別為：4、4、4 和 6。 因此，第三條路徑為優先選擇路徑。

2 優化路徑的遺傳算法

基于遺傳算法的高負載XMPP優化路徑主要求解流程如下：

（1）隨機產生初始種群，每個染色體采取實值編碼方式進行編碼；（2）計算個體適應度，判斷是否符合優化標準；

（3）采用自適應交叉，生產新的交叉染色體，選擇適應度高的生成新個體；

（4）采用自適應變異，產生新的變異染色體，選擇適應度高的生成新個體。

2.1 染色體編碼

簡化圖節點編號作為染色體的基因值。由圖2可以看出，簡化圖并不是一個完全連通圖，圖中許多節點之間并不存在邊，如節點1和節點2。因此根據簡化圖G,定義基因之間的約束關系如下：

（1）圖G中的邊的集合 E中任一邊（i，j），則定義基因 i與基因 j為一個基因對，記。基因對具有對稱性，若存在基因對，則必存在基因對。

（2）圖G中頂點集合V的任一頂點i，能夠與其配對的所有基因的序列，稱為該節點的鄰接基因序列。如圖2中節點8存在<8，4>、<8，7>、<8，9> 和<8，13>四個基因對，其對應的基因序列為{4，7，9，13}。

簡化圖中節點的自然路徑作為染色體，并采用自然編碼的方式對染色體編碼。一條染色體是由某些基因組成的序列geneSequence=（S1，S2，…，Sn），其中 Si∈V，（1≤i≤n），且滿足對 j（1≤j≤n-1），均是一個基因對。如染色體：

1→3→7→12→13→16

該路徑中存在以下基因對：

<1，3>，<3，7>，<7，12>，<12，13> 和 <13，16>。

由于路由路徑長度不一定完全相同，即不同染色體的長度并不完全相同，因此染色體長度為可變長度；另外，節點路徑中不存在回路，所以染色體長度不大于簡化模型G中頂點的總數17。

2.2 種群產生

文中采用帶基因序列約束的方法來產生隨機的初始種群，圖2使用隨機選擇節點的方法產生初始種群時發現，其中絕大多數個體并不是一條可行路徑。其算法流程如下：

輸入源節點：S；目標節點：O；節點數目：Num；總節點數：N，1≤S≤N，1≤O≤N

輸出染色體Gene=[Gene1,Gene2,… ,GeneNum]；

每個染色體Genei長度為Li,2≤Li≤N,1≤i≤Num

由基因對的具有對稱性，上述算法通過數組機制解決路徑中的回路問題。

2.3 適應度函數

文中遺傳算法中的個體對應于有權無向圖中求解的優化路徑。節點總數越少、權值總和越大的優化路徑認為是較優的個體，即權值節點比較大的路徑。因此，對于不同的個體設計如下適應度函數：

F(i,j)=Cmax-Σe(i,j)/Σf(i,j)，

其中，Σf(i,j)表示路徑上的所經過的節點數的總和，Σe(i,j)表示路徑上的所有權值的總和，Cmax=max(Σe(i,j)/Σf(i,j))+R，表示所有路徑中的最大權值節點比，其中隨機自然數R為修正因子。因此，路徑上經過的節點數少，總權值越大，適應函數的適應值越大；反之，越小。

2.4 選擇操作

本文采用輪盤賭[8]選擇方法進行個體選擇，個體適應度越大，被選中的概率越大。即優化路徑中經過的節點少并且權值大。表1是采用輪盤賭選擇方法，修正因子R取值為10，得到的節點1到節點16的路徑，具體如表1所示：

表1 節點1到節點16輪盤賭選擇路徑

其中P=F/ΣF。選擇染色體過程中產生的隨機數P∈[0,1]，按如下方法確定染色體：

當 P∈[0,0.26]，則選擇染色體 3→7→12→13；

當 P∈[0.26,0.51]，則選擇染色體 3→4→8→13；

當 P∈[0.51,0.72]，則選擇染色體 3→7→8→13；

當 P∈[0.72,1.00]，則選擇染色體 3→4→5→9→14→13

2.5 交叉操作

本文采用帶基因序列限制的交叉算子，具體描述如下：

假設進行交叉的父代個體P1、P2分別為：

P1：3→7→ |8→ 13

P2：3→4→ |5→ 9→14→ 13

首先隨機產生交叉位置 Location（1≤Location≤min（L1,L2）），其中L1和L2分別為P1和P2的染色體長度。假設Location=2，對染色體P1進行交叉操作時先判斷處于交叉位置Location后的染色體 P2中的基因是否存在于處于交叉位置Location的基因序列中，如果存在，則進行交叉；否則，依次向后尋找P2中的基因。同理，對染色體P2進行同樣的交叉操作。若P1與P2均不能進行交叉操作，則重新選擇一對染色體進行交叉。P1和P2交叉后的結果為：

P1’： 3→ 7→ |5→ 13

P2’： 3→ 4→ |8→ 9→ 14→ 13

交叉后的染色體中可能存在斷路，如染色體P1’。因此交叉后，需對染色體進行去環處理。

2.6 變異操作

本文采用對路徑中的子路徑進行變異的方法。首先，隨機確定產生變異的起點 S和終點T，然后通過調用產生初始種群算法，產生一條從S→T的路徑，再用該路徑替代原先路徑中S→T的路徑，作為變異后的新個體。

假設染色體為：3→ 4→ 8→ 9→ 14→ 13，不妨設變異起點為8，變異終點為9，通過調用產生初始種群算法產生一條8→9的路徑：

10

則變異后的結果為：

3→ 4→ 8→ 9→ 10→ 14→ 13

注意到產生變異后的新的染色體中可能存在環。因此，與交叉操作相同，變異后需對染色體進行去環處理。

3 試驗結果

假定初始種群大小為10，交叉概率為 PC=0.8，變異概率 Pm=0.01，進化代數為10，節點1到節點16的前4條路徑，其中最優路徑為3→7→8→13

表2 節點1到節點16的路徑列表

[1]P.Saint-Andre,Ed.Extensible Messaging and Presence Protocol(XMPP):Core[OL].http://www.faqs.org/rfcs/rfc3920.txt.

[2]黃劍.基于XMPP的端到端連接建立機制的研究與實現[D].國防科學技術大學，2009.

[3]張衛，張峻峰，羅長壽.XMPP應用于物聯網通訊協議的研究[J].中國農學通報，2012，28（09）：289-292.

[4]Liu Junli,Chen Shuangxi,Mao Jie.Genetic algorithm study on the university course timetabling problem[C]//2012 IEEE International Conference on Cyber Technology in Automation,Control,andIntelligent Systems(CYBER).Bangkok,Thailand,2012:179-182.

[5]張華，王進戈.機器人避開多隨機障礙物的路徑規劃遺傳算法[J].西華大學學報，2007，26(1)：56-58.

[6]Chang Wook Ahn,R.S.Ramakrishna.A Genetic Algorithm for Shortest Path Routing Problem and the Sizing of Populations [J].IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION Jun,2002:566-579.

[7]龔正虎，黃劍，侯婕.基于XMPP的多跳TCP連接通信方案研究[J].北京工業大學學報，2008，34(Supp):32-35.

[8]梁宇宏，張欣.對遺傳算法的輪盤賭選擇方式的改進[J].信息技術，2009，12(12):127-129.