基于粒子群優化核獨立分量的特征降維算法及其應用研究
孫 磊,賈云獻,王衛國,張英波,趙勁松,3
(1.軍械工程學院裝備指揮與管理系, 河北石家莊 050003; 2.軍械工程學院科研部, 河北石家莊 050003;3.軍事交通學院裝備保障系, 天津 300161)
為了更好地掌握裝備的運行狀態,在對裝備實施狀態監測時往往采集多種狀態信息[1]。例如:對于油液光譜分析采集的元素種類多達20幾種,這些狀態信息間存在一定的相關性,若把這些狀態信息直接用于裝備的剩余壽命預測將導致計算量急劇增大或難以計算,而且由于引入了與裝備狀態相關度較小的狀態信息而導致結果存在偏差。因此,如何從大量狀態信息中提取影響裝備壽命的主要特征信息,使得這些特征信息間既充分反映原來的狀態信息的作用又彼此相互無關,就顯得十分重要,為下一步的故障診斷與預測提供有效特征值[2-3]。
獨立分量分析(independent component analysis,ICA)是近年來在信號分析與處理中發展形成的一種數據處理方法[4]。ICA作為一種有效的盲源分離技術仍是信號處理領域的熱點,但目前的算法在處理非線性變化的信號時還有一定的局限,而基于非線性函數空間的ICA方法——核獨立分量分析(kernel independent component analysis,KICA)[5]則可以解決這一問題。KICA方法具有更好的靈活性和魯棒性,不僅能夠實現高維非線性數據的降維,更重要的是,基于信號的高階研究信號間的獨立關系使經過變換所得到的各個分量之間不僅正交,而且相互獨立,避免了數據的非線性對預測模型的影響[6-7]。
由于KICA算法精度受到核函數類型及其參數的影響,因此選擇合適的核參數至關重要。目前核參數的選擇方法仍是主要靠大量的試驗人為確定或采用交叉檢驗的辦法,不但費時費力效率低,而且這樣確定的核函數參數不一定是最優的。因此,對KICA核函數參數的優化方法進行研究,對改善其特征降維結果具有重要的意義。粒子群優化算法(particle swarm optimization,PSO)是一種全局并行的尋優方法,近年來已在函數優化、自動控制、機器學習、人工生命等領域都得到了廣泛的應用[8-9]。筆者針對KICA技術在核函數參數選擇上的盲目性,首先利用Fisher判別函數的思想建立核函數的參數優化的適應度,進而基于PSO算法求出核函數參數優化模型的全局最優解,改善KICA的性能。最后通過案例驗證了方法的可行性與有效性。
1 獨立分量分析
假設S=[s1,s2,…,sn]T為n個相互獨立的源信號,X=[x1,x2,…,xn]T為m個觀測信號,其滿足以下關系[10]:
X=AS。
式中:A為m×n階矩陣,該式表示了觀察所得的狀態變量是如何由獨立分量構成的。目的是通過觀測數據x估計未知獨立源s和混合矩陣A,即求解一個解混矩陣W,使得
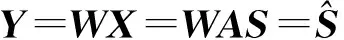
的各分量相互獨立,并把Y作為S的估計。獨立分量分析中所有的出發點都是一個基本假定:即認為這些獨立分量si互相統計獨立,且不服從高斯分布。若記Y=WTX,則可以通過最大化WTX的非高斯性來求W,從而求得獨立分量Y。
2 核獨立分量分析
2.1 Mercer核
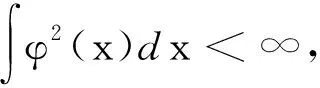
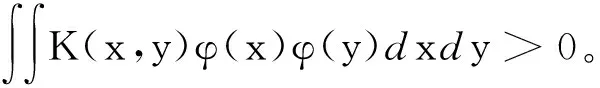
事實上任何一個函數只要滿足Mercer條件,就可以用作Mercer核,同時可以分解成特征空間的點積形式。假設輸入空間的樣本xk∈RN,k=1,2,…,l,被某種非線性映射φ映射到某一特征空間R,得到φ(x1),φ(x2),…,φ(xl)。那么輸入空間的內積運算,在特征空間就可以用Mercer核表示為K(xi,xj)=φ(xi)·φ(xj)。
2.2 KICA算法步驟
輸入:數據矢量x1,x2,…,xn和核函數K(x,z)。
1)對輸入數據矢量x1,x2,…,xn進行預白化處理,使輸入的向量之間相互正交。
2)利用Cholesky分解求出原始獨立數據z1,z2,…,zn的Gram矩陣K1,K2,…,Km,其中zi=Wxi,W為獨立分量分析中的解混矩陣。
3)定義λH(K1,K2,…,Km)為下式的最大特征值:
(1)
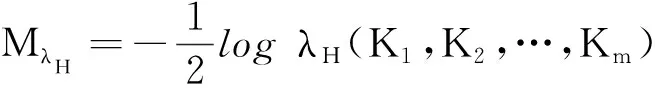
輸出:W矩陣。上面的算法不斷在步驟2)和4)之間重復運行,直到滿足了收斂性的條件便可以得到解混矩陣W,W為m×n階(m 圖1 粒子位置更新示意圖Fig.1 Scheme of particle position updating PSO算法將每個優化問題的潛在解看作是搜索空間的粒子,每個粒子都有一個被優化函數決定的適應值和一個決定其運動方向和距離的速度向量,然后粒子群就追隨當前的最優粒子在解空間進行搜索[11]。PSO初始化為一群隨機粒子,通過不斷迭代搜索最優解。在每一次迭代中,粒子通過跟蹤2個極值來更新自己,一個就是粒子本身到當前時刻為止找到的最優解,稱為個體最優值;另一個就是整個種群到當前時刻找到的最優解,稱為全局最優值,粒子位置更新過程如圖1所示。 圖中:xid(t)為第i個粒子的當前位置;vid(t)為第i個粒子的當前速度,vid∈[-Vmax,Vmax],Vmax是最大限制速度,非負;pid(t)為第i個粒子迄今為止搜索到的最優位置;pgd(t)為整個粒子群搜索到的最優位置。 假設在一個D維的目標搜索空間中,有m個粒子組成一個群體,其中第i個粒子的位置表示為向量xi=(xi1,xi2,…,xiD),i=1,2,…,m,其速度也是一個D維的向量,記為vi=(vi1,vi2,…,viD)。第i個粒子迄今為止搜索到的最優位置為pi=(pi1,pi2,…,piD),整個粒子群搜索到的最優位置為pg=(pg1,pg2,…,pgD),粒子更新公式如下[12]: vid(t+1)=vid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t)); (2) xid(t+1)=xid(t)+vid(t+1)。 (3) 將式(2)稱為基本粒子群優化算法。其中,當vid>Vmax時,取vid=Vmax;當vid<-Vmax時,取vid=-Vmax;i=1,2,…,m;d=1,2,…,D;加速常數c1和c2為非負常數;r1和r2服從[0,1]上的均勻分布隨機數。 大量數值實驗表明,核參數的取值對基于核函數的特征降維算法性能具有很大的影響。例如:高斯徑向基核函數σ過大,樣本“勢力范圍”也會過大,以致一些毫無關系的訓練樣本會干擾對新測試樣本作出正確判斷;σ過小,則會導致核學習只有記憶功能而無法對新樣本進行判斷[13]。所以選擇合適的函數寬度需要在兩者之間進行權衡。 根據前面的分析,KICA的主要思想是使得各分量的數據點散布于最大統計相關方向,強調的是分解出來的各分量之間的相互獨立性。而Fisher線性判別分析(fisher linear discriminant analysis,FDA或LDA)的基本思想是選擇使得Fisher準則函數達到極值的向量作為最優投影方向,把原始數據沿該方向進行投影得到一條直線,使投影后不同類別的數據盡可能分開,相同類別的數據則盡可能的聚集,即投影后模式樣本的類間散布最大而類內散布最小。因此,基于KICA和FDA基本思想之間的相通性,可以借鑒FDA的思想來探索KICA中核參數優化方法。 1)建立核參數優化適應度函數 設X1,X2,…,XD是特征空間D個樣本類,特征樣本X為n維實向量,即X∈Rn,經過非線性映射Φ后對應樣本向量為Φ(X)∈H。則樣本類Xi在特征空間的均值向量為 (4) 式中,ni為第i個樣本類的樣本數。 定義樣本的類間散度Sb為 (5) 定義樣本的類內散度Sw為 (6) 式中,Φ(xij)表示特征空間H中第i類第j個樣本。對于高斯徑向基核函數,由于k(xij,xij)的值等于1,所以對高斯徑向基函數式(6)可以簡化為 (7) 那么,根據Fisher極小鑒別準則,在此建立適應度函數為 (8) 實驗表明,對于完全非線性可分問題,Fisher鑒別函數F(w)的極小值點w*存在[14]。對于高斯徑向基核函數把w*作為參數σ的值可以取得較好的效果;而對于多項式核函數則把w*作為多項式的階次d的取值。對于線性可分或幾乎線性可分問題,隨著w由小變大,F(w)值急劇下降,然后趨于平穩,此時可以取F(w)開始趨于平穩時的w作為w*。 2)KICA算法中核參數的粒子群優化過程 在實現核參數優化過程中,對于適應度函數式(8),需要求Fisher鑒別函數F(w)的極值點。F(w)有可能是多峰值函數,存在多個極值點。為了得到全局最優值,在此結合PSO算法對參數w進行優化,建立PSO-KICA算法流程,如圖2所示。具體步驟如下。 輸入:數據樣本x1,x2,…,xn,選擇核函數K(x,z)。 圖2 PSO-KICA算法流程Fig.2 Flow chart of PSO-KICA 1)計算樣本的類間散度Sb和類內散度Sw; 2)構建Fisher鑒別函數F(w)作為粒子群優化的適應度函數; 3)給定核參數w的取值范圍(wmin,wmax)、種群規模m、加速常數c1和c2、最大進化代數Tmax、最大限制速度Vmax、慣性權重ω和計算精度ε。 4)隨機產生初始群體,計算個體適應度值Fp和種群整體適應度值Fg; 5)對粒子的位置和速度進行更新; 6)判斷迭代次數t是否達到最大進化代數Tmax或評價值小于給定精度ε。如果達到最大進化代數Tmax或評價值小于給定精度ε,得到最優核參數w; 7)利用優化的核函數實現KICA算法。 輸出:根據z=Wx分離出相互獨立的信號。 由于自行火炮發動機工作條件復雜多變、工作環境相對惡劣,對其進行狀態監測往往采用油液分析方法提取潤滑油中金屬元素的成分和濃度。然而,油液數據大多具有高維、非線性特點,不利于進一步的分析處理,人們往往采用降維的手段對其進行分析處理。 為驗證上述所建立的基于粒子群優化算法的核獨立分量分析技術的可行性和有效性,采用油液光譜分析的監測方式采集某型發動機潤滑油中各元素的濃度為狀態信息[15]。筆者重點收集了該發動機潤滑油中鐵、鋁、鉛、硼、鋇、鉻、鎂、硅等8種元素濃度值。圖3是原始的油液光譜分析數據散點圖(由于篇幅所限僅給出Fe元素和Al元素的濃度散點圖)。 圖3 Fe元素和Al元素濃度散點圖Fig.3 Graphical of iron and aluminum oil concentration records 基于油液濃度數據,采用PSO算法對KICA中的高斯徑向基核函數參數進行優化,確定KICA分析的最優核函數,參數收斂過程如圖4所示。可見,當核函數參數進化到50代時,適應度函數已收斂到規定的精度要求并逐漸趨于穩定,且核函數寬度也逐漸收斂于1。即當高斯徑向基核函數σ=1.07時,適應度函數F(w)取得最優值為3.428 6。 圖4 基于PSO的高斯徑向基核函數參數優化Fig.4 Parameter optimizion of gausion kernel function based on PSO 圖5 油液濃度數據特征降維結果Fig.5 Feature dimension reducing result of oil concentration data 圖6 原始油液梯度數據投影和梯度數據KICA投影Fig.6 Projective and KICA projective chart of oil concentration data 得到最優核函數之后,根據前述降維算法對發動機油液濃度數據進行降維分析與處理,得到了3個獨立主成分,如圖5所示。圖6a)是油液濃度數據進行PSO-KICA算法降維后,前3個獨立成分在空間的投影圖,可見各個分量之間具有較好的獨立性。而未經KICA分析處理的原始數據則存在較大的相關性,如圖6b)所示。利用PSO-KICA算法對油液濃度數據進行處理的過程表明,該算法不僅避免了核函數參數選擇過程的盲目性,而且實現了高維非線性數據的降維,得到了相互獨立的特征分量。 針對KICA特征降維算法在核函數參數的選擇上存在的問題,利用PSO算法實現了核函數參數的優化,建立了基于PSO-KICA的特征降維算法。通過對某自行火炮發動機油液濃度數據進行降維處理,達到了基于PSO-KICA降低特征向量的維數的目的,驗證了該方法用于特征降維的可行性和有效性。 參考文獻/References: [1] JARDINE A K S,LIN D,BANJEVIC D. A review on machinery diagnostics and prognostics implanting condition-based maintenance[J]. Mechanical System and Signal Processing, 2006, 20(1): 1 483-1 510. [2] ABRAHAM B,MEROLA G. Dimensionality reduction approach to multivariate prediction[J]. Computational Statistics and Data Analysis, 2005, 48(1):5 016. [3] 歐陽曉黎,張延生,楊 軍. 復雜電子裝備智能故障診斷方法[J]. 河北科技大學學報, 2004,25(2):42-49. OUYANG Xiaoli,ZHANG Yansheng,YANG Jun. The intelligent fault diagnosis methods for complex electronic equipments[J]. Journal of Hebei University of Science and Technology, 2004, 25(2):42-49. [4] COMON P. Independent component analysis-a new concept[J]. Signal Processing, 1994(36):287-314. [5] 胥永剛, 李 強, 王正英, 等. 基于獨立分量分析的機械故障信息提取[J]. 天津大學學報, 2006, 39(9) :1 066-1 071. 一篇好的文章,里面的語法必須要使用規范。學生在英語寫作當中必須要注意語法的使用,如果出現了語法錯誤,那么整個句子就達不到所要表達的意思,當然,所有的章節也會失去本身的含義。 XU Yonggang, LI Qiang, WANG Zhengying, et al. Fault information extraction of mechanical equipment based on independent component analysis[J]. Journal of Tianjin University, 2006, 39(9):1 066-1 071. [6] FAUVEL M,CHANUSSOT J,BENEDIKTSSON J A. Kernel principal component analysis for feature reduction in hyperspectral images analysis[A]. Proceedings of the 7th Nordic[C].[S.l.]: Signal Processing Symposium, 2006.238-241. [7] XU Anbang, JIN Xin, GUO Ping. KICA feature extraction in application to FNN based image registration[A]. 2006 International Joint Conference on Neural Networks[C].[S.l.]:[s.n.], 2006.3 602-3 608. [8] 高 峰,武 睿,劉南平.基于自適應蚊群算法的無線傳感器網絡能量優化[J]. 河北工業大學學報, 2010,39(16):4-7. GAO Feng,WU Rui,LIU Nanping.An approachto WSN energy optimization based on self-adaptive ant colony algorithm[J]. Journal of Hebei University of Technology, 2010,39(6):4-7. [9] 李正濤,趙環宇,馬獻果. 應用粒子群算法從已知數據中確定置信測度和似然測度[J]. 河北科技大學學報,2011, 32(2): 128-132. [10] BACH F R, JORDAN M I. Kernel independent component analysis[J]. Machine Learning Research, 2002(3): 1-48. [11] 何學文. 基于支持向量機的故障智能診斷理論與方法研究[D]. 長沙:中南大學, 2004. HE Xuewen. Research on Fault Intelligent Theory Based on SVM [D]. Changsha: Central South University, 2004. [12] KENNEDY J,EBERHART R. Particle swarm optimization[A]. Proc IEEE Int'l Conf on Neural Networks, IV. Piscataway[C]. NJ: IEEE Servive Center, 1995. 1 942-1 948. [13] 魏秀業. 基于粒子群優化的齒輪箱智能故障診斷研究[D]. 太原:中北大學,2009. WEI Xiuye. Study on Intelligent Fault Diagnosis of Gearbox Based on Particle Swarm Optimization [D]. Taiyuan:North University of China, 2009. [14] 褚蕾蕾, 陳綏陽, 周 夢,等. 計算智能的數學基礎[M]. 北京: 科學出版社, 2002. CHU Leilei, CHEN Suiyang, ZHOU Meng,et al. Mathematics Foundation of Computation Intelligent[M]. Beijing: Science Press, 2002. [15] 陳 麗. 基于狀態的維修模型及應用研究[D]. 石家莊:軍械工程學院,2009. CHEN Li. Condition Based Maintenance Model and Application[D]. Shijiazhuang :Ordance Engeerning College, 2009.3 基于粒子群優化算法的核獨立分量分析技術
3.1 基本PSO算法
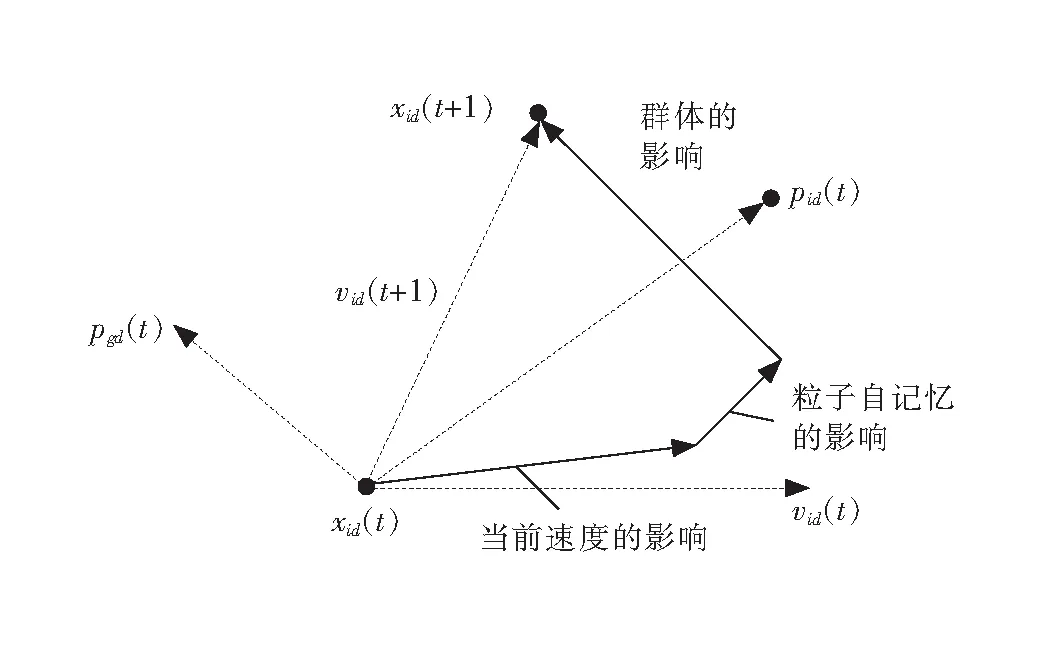
3.2 基于PSO的核函數參數優化方法
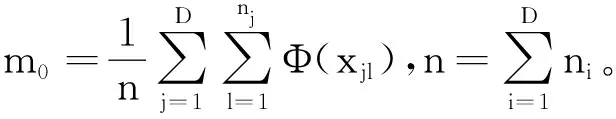
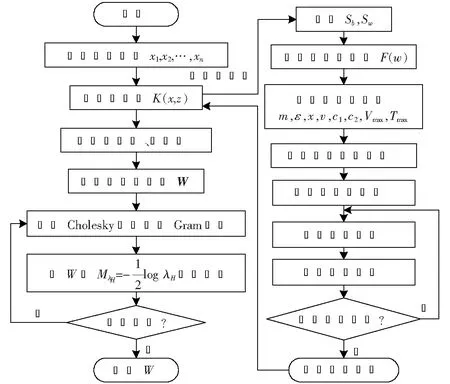
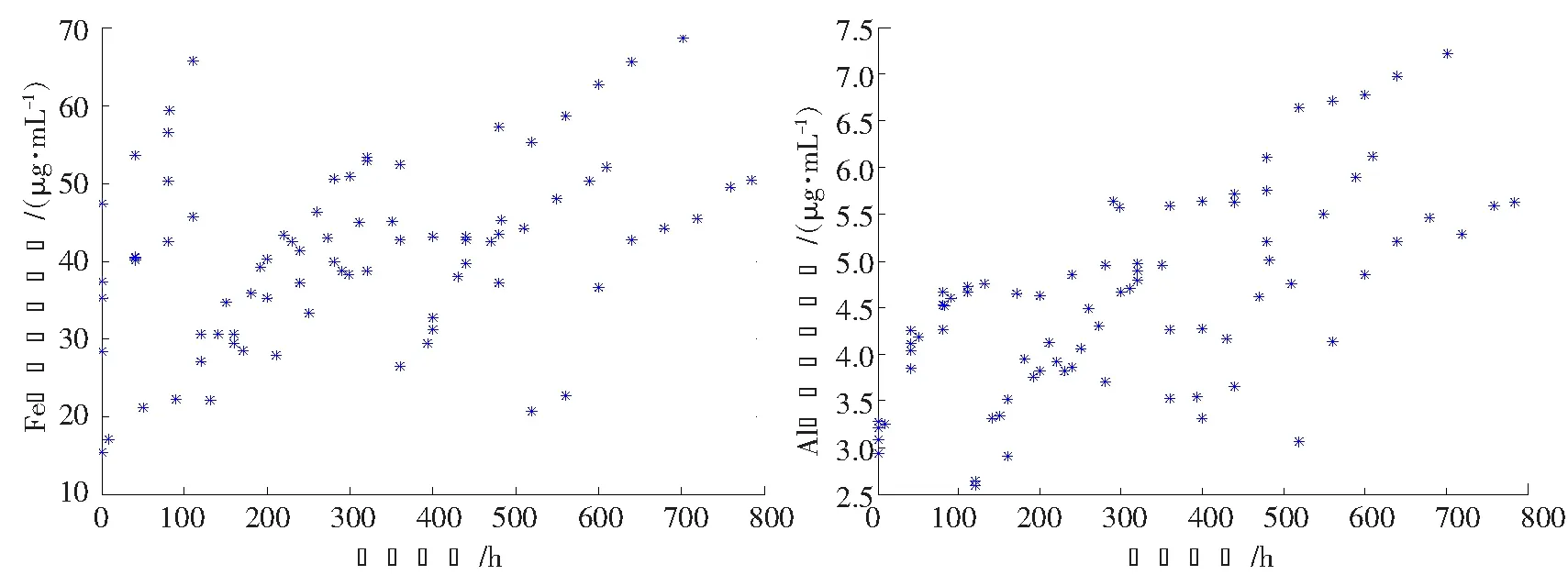
4 案例分析
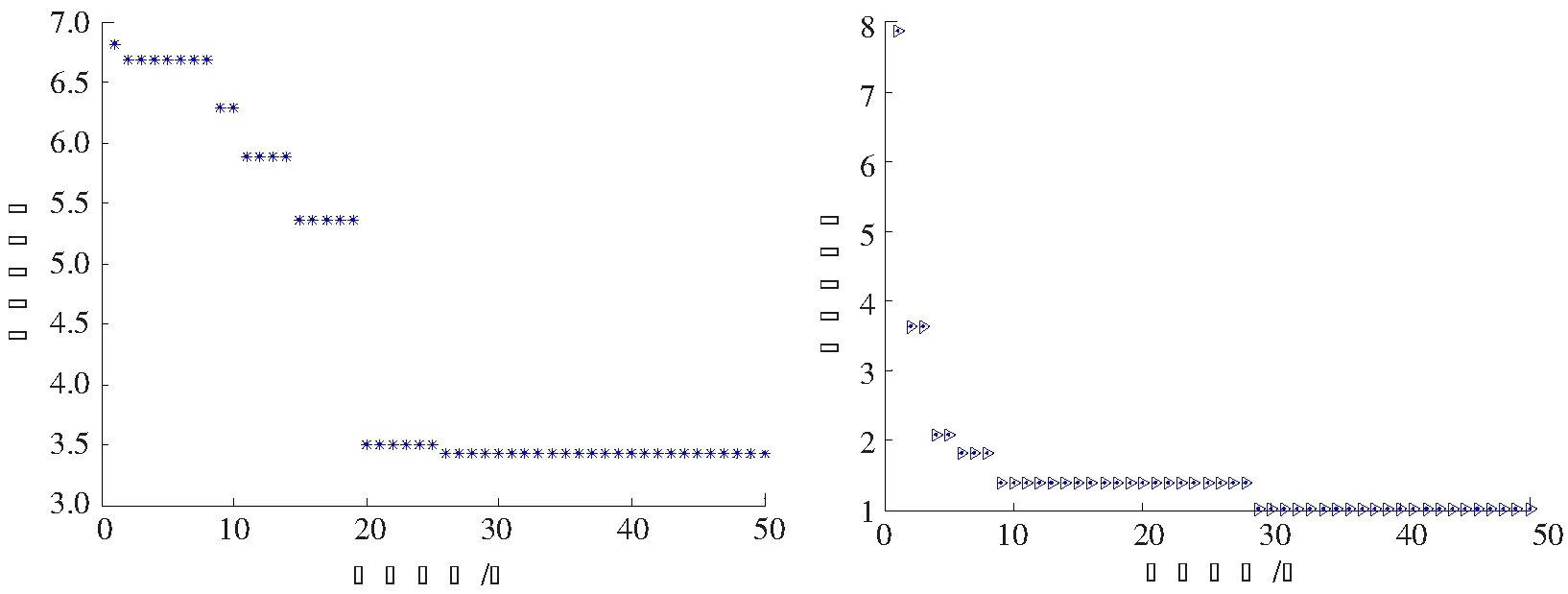
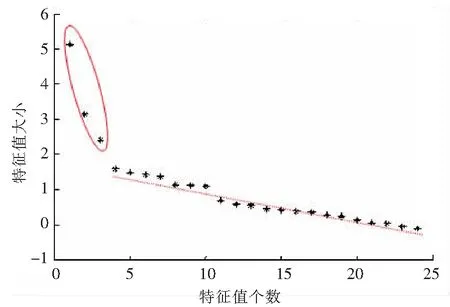
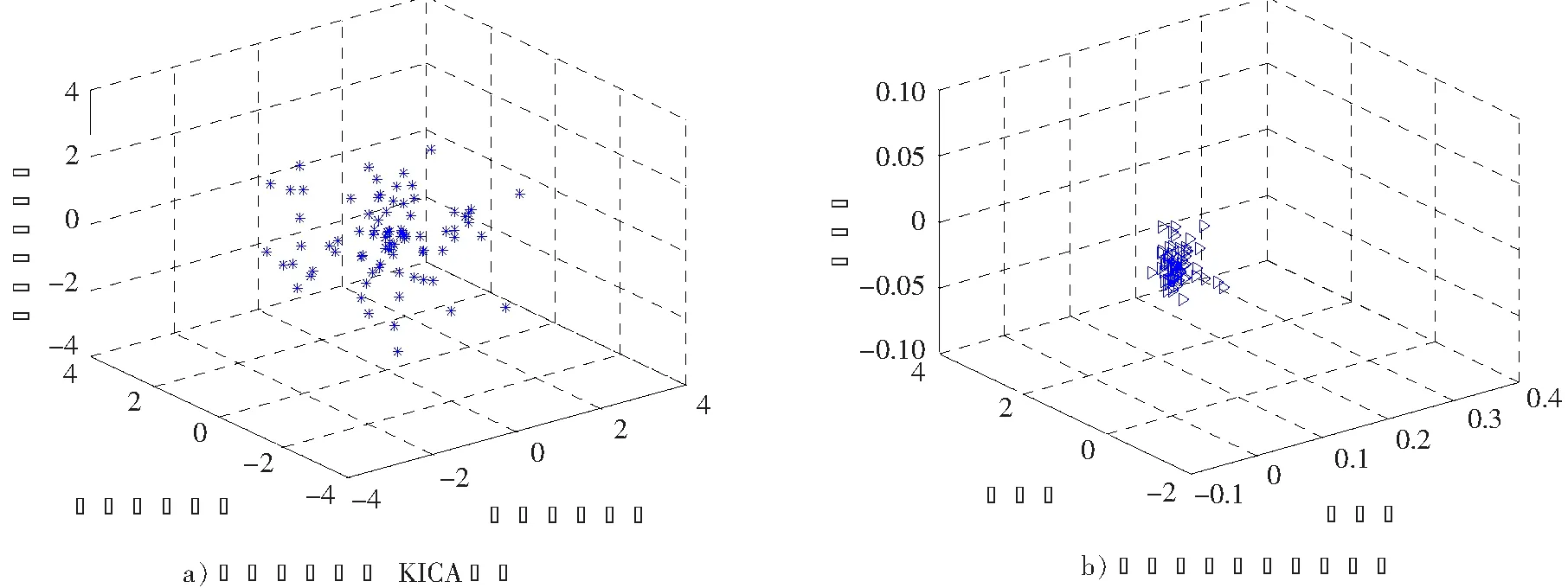
5 結 語

