埋深對礦山壓力影響的常微分方程解法研究

郭海英，王長建

(1.山西陽泉固莊煤礦，山西 陽泉 045060;2.河南理工大學能源學院，河南 焦作 454000)

在大多情況下，礦山壓力顯現會對采礦工程造成不同程度的危害。為了使礦山壓力顯現對正常的采礦工作不產生影響，必須采取各種措施把礦山壓力顯現控制在一定范圍內。以避免造成巨大的人員傷亡和財產損失。因此，事先對各個煤層處的礦山壓力進行估測顯得越來越重要。

礦山壓力現場觀測研究法是在生產現場對礦山壓力大小進行觀測和記錄，利用各種儀表、工具觀測采場圍巖變形、位移、頂底板破壞、支架受載荷及壓縮等情況，然后從動態分析中得出對采場礦山壓力顯現有顯著影響的巖層運動的條件、時間和方向以及采場周圍支承壓力的變化狀況，為解決現場礦山壓力控制問題提供依據。由于現場觀測獲得的資料反映多種因素的相互作用，用已經測得淺部礦山壓力數據預測深處礦山壓力的大小，具有可靠方便的特點。故利用這種資料預測分析深部礦山壓力大小較為可靠，效果顯著，越來越為生產現場認可采用。

為此，本文運用常微分方程的數值解為方法，根據實驗數據，研究得出煤炭埋深與其所受礦山壓力大小的變化規律，進而對煤炭埋深處的礦山壓力值進行預測，為煤炭開采時開挖巷道所需支護強度進行預測并提供理論依據。

1 問題分析

某煤礦煤炭賦存深度平均約為500 m，現在需要初步預測煤層處所受的礦山壓力大小。根據煤層上方0～50 m測量得到一組數據，見表1，根據測得的數據得到此處礦山壓力大小，大體可用微分方程x2+x－y來表示，其中y是井下某煤層處的礦山壓力，x是對應的煤層埋深，且假定地表平面的壓力為零。

2 常微分方程的數值解法

常微分方程(組)的解是一個函數或一族函數。所謂數值解法就是尋求解函數自變量的一系列離散點上的近似值。常微分方程的數值解法很多，常用的是歐拉公式。考慮微分方程的初值問題:

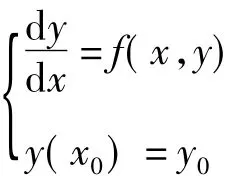
把微分方程中的導數用折線的斜率代替，得到:

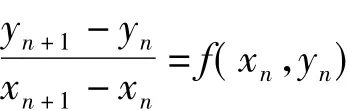
假設對于不同的n有xn+1－xn相同，記為h=xn+1－xn得到yn+1=yn+hf(xn，yn)基本的歐拉公式，其中，h稱為步長。

3 算法的Matlab實現

3.1 實驗數據

在本實驗中，礦山工作人員已測得u在50 m內的礦山壓力大小，見表1。

表1 50 m內礦山壓力大小測量值

3.2 Matlab程序代碼

常微分方程數值解法Matlab程序:

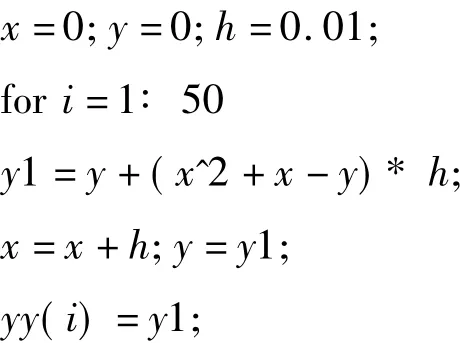
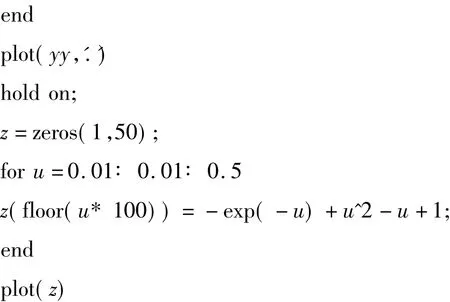
4 計算結果及分析

4.1 計算結果

為了便于對實驗數據和數值解進行比較，在此把實驗中得到的兩種數據放在一起，具體數據見表2。

表2 不同u值得到的兩種解析值和數值

4.2 Matlab圖形

歐拉公式計算的數值解與解析解示意圖見圖1。

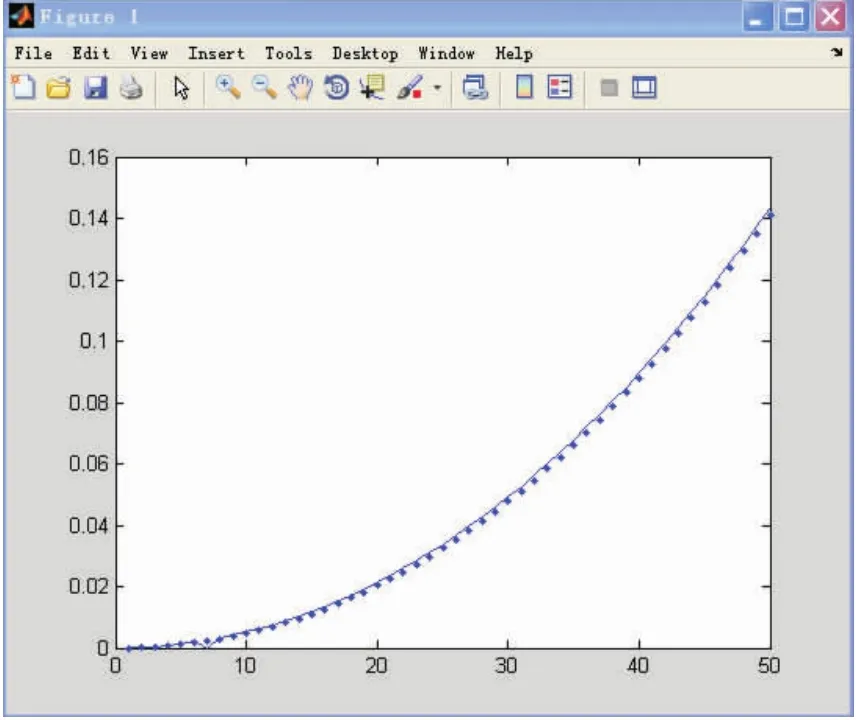
圖1 歐拉公式計算的數值解與解析解示意圖

4.3 結果分析

從表2和圖1可知，用數值法得到的數據與用解析方法得到的數據基本是一致的，當u=5時，誤差為3，當u=50時，誤差為25。隨著u的增大，數值解與解析解的誤差也逐漸增大，但是變化量比較小。從圖1可以看出，隨著埋深的增大，礦山壓力的值越來越大，而且，開始時礦山壓力增加比較緩慢，深度越大礦山壓力增長越快。由此得出的礦山壓力變化情況，進而得出不同埋深處所受礦上壓力的大體范圍。在此可以預測u為500 m時，礦山壓力值為21 MPa。

5 結論

本文運用常微分方程數值解法，分析了埋深變化對礦山壓力的影響，根據預測方程得出了不同埋深與其所受礦山壓力大小的關系，結果表明:

1)不同埋深的煤層所受的礦山壓力大小不同，埋深越深，所受到的礦山壓力越大。

2)在一定范圍內，可以根據較淺深度的礦山壓力值預測較深處的礦山壓力大小，預測結果與真實值比較接近。

［1］錢鳴高，石平五，許家林.礦山壓力與巖層控制［M］.徐州:中國礦業大學出版社，2010:353－371.

［2］王高雄，周之銘.常微分方程［M］.北京:高等教育出版社，2006:19－21.

［3］孫 祥，徐流美，吳 清.matlab7.0基礎教程［M］.北京:清華大學出版社，2005:382－385.

［4］王 輝.大埋深采煤工作面礦壓特征的數值模擬［J］.煤炭科學技術，2010(6):73－75.