基于Gompertz模型的公路交通量分析與預測

朱學坤，彭婷婷

（江西交通職業技術學院，江西 南昌 330013）

0 引言

公路交通量是經濟社會發展對公路交通需求的反映，其發生和發展與沿線的經濟社會狀況密切相關。交通量分析與預測是公路建設項目可行性研究階段的重要工作，是確定公路等級、工程規模，進行經濟評價和項目后評價的基礎[1]。

公路建設項目的交通量分析與預測方法有很多，一般采用以汽車出行起訖點矩陣（簡稱“OD表”）為基礎的“四階段預測法”。眾所周知，對公路建設項目實施交通量OD調查，存在資料不全、技術復雜、影響因素多和組織難度大等問題，對低等級公路而言，特別是縣鄉公路，若采用上述方法既費時又費力，經濟上不可取。交通量預測工作應適當簡化或采用其他預測方法。本文采用基于時間序列模型的預測方法，通過對三種模型的分析與對比，綜合評價確定適合于交通量發展規律的預測方法。

1 時間序列模型的建立

時間序列模型預測方法是以交通量作為研究對象，即對交通量隨時間變化規律的預測，目前主要有以下幾種預測模型：二次多項式曲線、指數曲線和Gompertz曲線。

1.1 二次多項式曲線模型

二次多項式曲線預測方法屬于趨勢外推法，是將預測對象具有變動趨勢的歷史數據擬合成一條拋物線曲線，通過建立拋物線曲線模型進行預測的方法，適合于中長期的數據預測，其模型為：

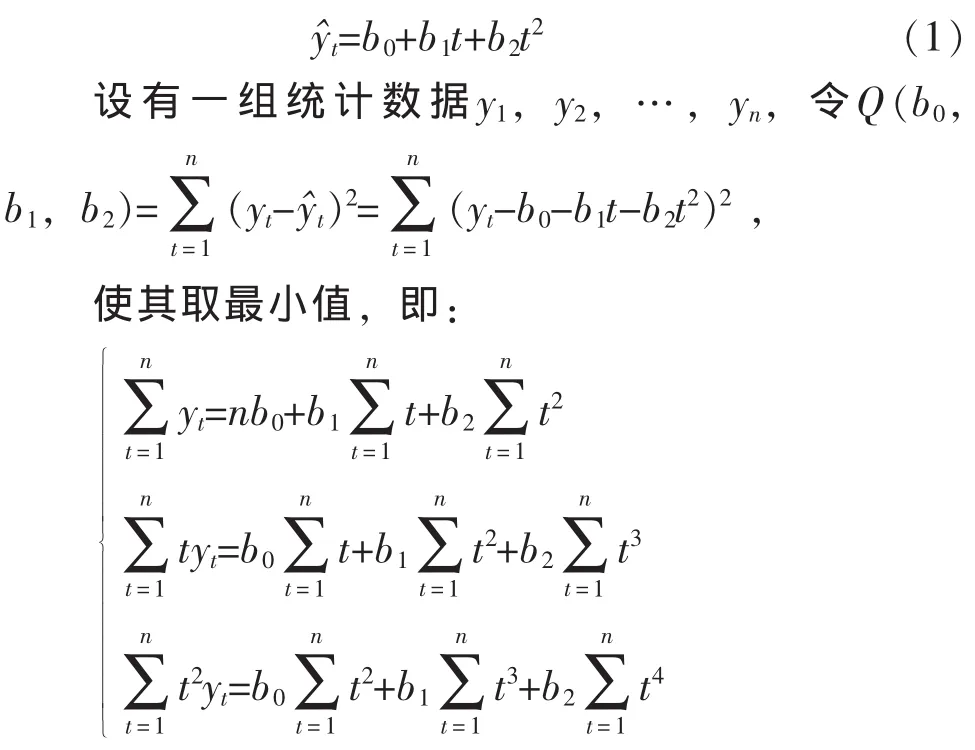
1.2 指數曲線模型

指數曲線預測法又稱指數曲線外推法或簡單外推法，是指對符合指數增長規律的一組觀測數據，建立指數曲線方程，以此作為預測的數學模型來推測預測事件的未來發展趨勢與狀態的方法，其模型為：

兩邊取對數，得：

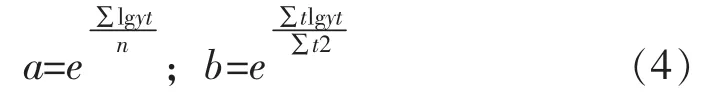
1.3 Gompertz曲線模型

Gompertz曲線模型屬于生長曲線，它反映了時間序列呈現S型增長曲線，是一種用于中長期預測方法，其模型為：

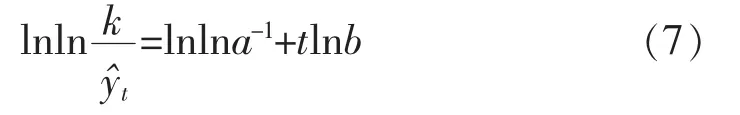
2 三種時間序列模型的對比

二次多項式曲線預測模型是研究時間序列觀察值數據隨時間變動呈現一種由高到低再到高（或由低到高再到低）的趨勢變化的曲線外推預測方法。由于時間序列觀察值的散點圖呈現拋物線形狀，故也稱之為二次拋物線預測模型。該方法預測曲線存在拐點，當t=-b1/2b2時，y=（4b2b0-b12）/4b2，y為最大值或者最小值。在交通量預測中，公路交通量隨著交通條件的改善、國民經濟水平的提高、人們出行需求的增長而呈現出增長的趨勢。若該拋物線曲線為凸型曲線，則-b1/2b2＞0，y值由低到高再到低；若該拋物線曲線為凹型曲線，則3b2+b1＞0，y值由高到低再到高、顯然，根據以往公路的交通量發展，這不太符合事實，所以對交通量預測而言，二次多項式曲線只適合于中期預測，且需經過論證后才方能采用。

指數曲線預測模型在交通量預測方面的運用，主要是針對交通量隨著時間的變化按同一增長率不斷增加或減少的變化趨勢，利用其時間數據資料，擬合成指數曲線，建立模型并進行預測的一種方法。但實際上，交通量在20年內不可能按同一增長率增長，且增長率還可能為零，所以該預測方法一般只適用于短期預測。

Gompertz曲線模型又稱S曲線，是增長曲線的一種形式，該曲線具有以下性質[2]：

a）k＞0，lna＜0，0＜b＜1；

b）曲線通過點（0，ka）；

c）曲線以y=0和y=k為漸近線；

因此，該曲線呈現出初期增長緩慢，接著以較大幅度增長，隨后趨于穩定水平的趨勢，符合產品生命周期的發展趨勢。針對公路本身而言，預測基年及建成后兩三年，由于公路投產后存在適用期，且人們對新鮮事物有延后反應，所以公路交通量在建成初期增長較為緩慢，緊接著呈現較大幅度的增長速度；當公路運營到一定時期，交通量將趨于飽和，此時交通量呈水平方向發展。公路作為一種公共產品，也同樣有著生命周期，采用Gompertz曲線模型能較好地符合交通量發展的規律。

3 結合實例預測分析

采用時間序列預測模型對交通量進行預測時，年份是自變量，交通量為因變量。在有近期交通量的歷史資料的前提下，可利用時間序列預測模型進行交通量未來年的預測。

現以省道319線為例。目前該省道為三級公路（2005～2011年公路交通量數據見表1），根據公路網規劃，其遠景規劃為二級公路。本文在工程可行性研究階段對交通量進行了預測實證分析，分別采用二次多項式曲線、指數曲線和Gompertz曲線模型進行20年的交通量預測。

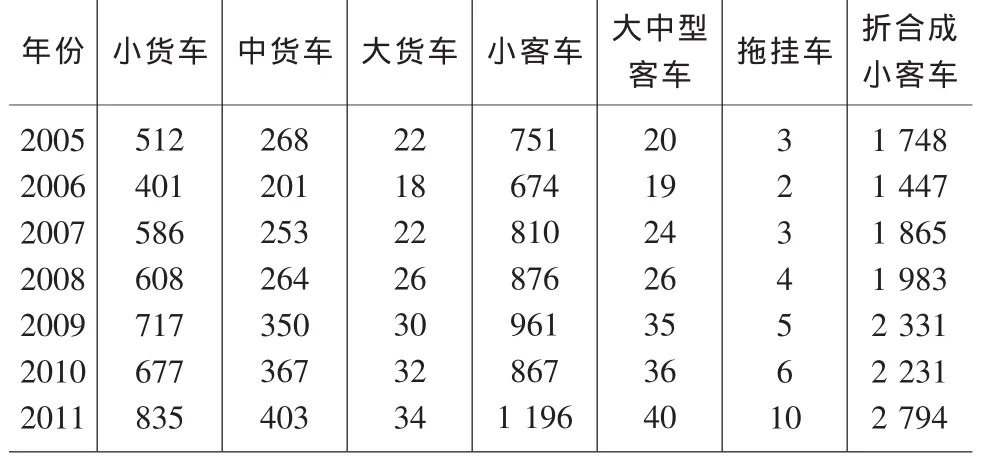
表1 省道319線2005-2011平均日交通量 單位：輛

3.1 二次多項式曲線模型

對表1中交通量和年份進行二次多項式曲線回歸，得到：

式中，b0=1631，b1=-23.857，b2=26.071。 年份t的取值規定：2005年為1，2006年為2，2007年為3，依次類推。經計算，相關系數R2=0.874，該曲線為凹型，t=0時，y=1631，拐點處t=0.458，則從2005年開始，交通量一直呈遞增函數增長。

3.2 指數曲線模型

對表1中交通量和年份進行指數曲線回歸，得到：

式中，a=1412.2，b=0.0891，年份t的取值規定：2005年為1，2006年為2，2007年為3，依次類推。

經計算，相關系數R2=0.8104，t=0時，y=1412（交通量取整），該方程為遞增函數，表明從2005年開始，交通量一直呈增長趨勢。

3.3 Gompertz曲線

對表1中交通量和年份進行Gompertz曲線回歸，得到：

式中，k=25000，a=0.055，b=0.965。年份t的取值規定：2005年為1，2006年為2，2007年為3，依次類推。經計算，相關系數R2=0.9216，t=0時，y=1375，當t=30（即在2034年）時，曲線到達拐點，此時y=9197，表明從2005年開始，交通量一直呈增長趨勢，到2034年開始趨于穩定，y值的極限值趨近于25000。

利用上述得到的三個模型預測未來特征年的交通量如表2所示。

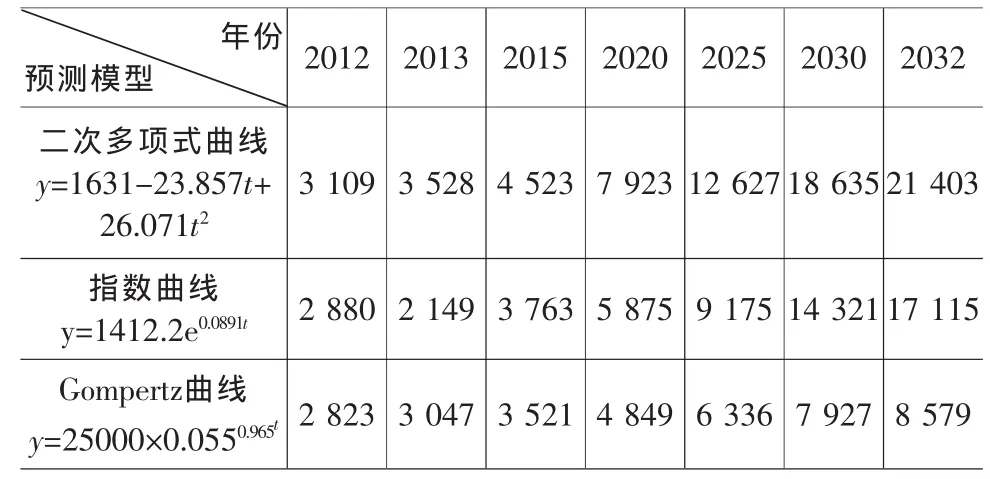
表2 省道319線未來特征年的交通量預測結果 單位：輛

4 結語

交通需求預測理論日益成熟和完善，高等級公路建設項目可行性研究中的交通需求預測方法一般采用“四階段預測法”，但預測過程過于復雜，涉及因素太多，而且預測結果并非完全可靠。對低等級公路而言，從簡單、有效等方面分析和研究適合低等級公路的交通量預測理論和方法更具有現實意義。本文正是從這些實際問題出發，深入分析和研究了公路建設項目可行性研究中的交通預測方法，期望能對低等級公路建設項目可行性研究提供一種科學合理可行的交通預測方法。

本文所建立的預測模型，通過對二次多項式曲線預測模型、指數曲線預測模型、Gompertz曲線預測模型的對比分析，發現前兩種預測模型相關系數較差，預測結果明顯偏大，而Gompertz曲線符合產品生命周期的特點，且相關系數較好，比較符合公路交通量的發展規律，具有其它預測法無法具備的優勢。通過實例分析可以看出Gompertz曲線模型的預測精度要明顯優于其它預測模型的精度，與遠景規劃相適應，因此可認為該模型比較適合交通量預測。

[1]交通運輸部.公路建設項目可行性研究報告編制辦法[S].北京：人民交通出版社，2010.

[2]劉云哲，何顯慈.公路運輸項目可行性研究[M].北京：人民交通出版社，1998.

[3]廖向東，高波.三峽翻壩運輸江南公路交通量預測思路探討[J].公路，2007，（12）：103-108.

[4]童明榮，薛恒新，林琳.基于季節ARIMA模型的公路交通量預測[J].公路交通科技，2008，（1）：124-128.

[5]彭利人，王樹東，馮艷春.公路交通量預測可靠性問題研究[J].交通標準化，2008，（8）：119-122.

[6]周榮康，徐永，李若靈.基于灰色殘差GM（1，1）模型的道路交通量預測的研究[J].交通運輸工程與信息學報，2008，（3）：49-52.

[7]程國宏.縣鄉公路交通量預測方法研究[J].華東公路，2007，（5）：74-76.